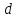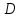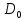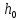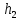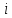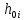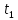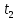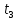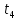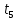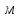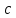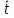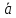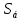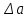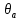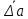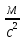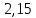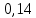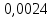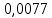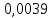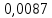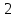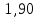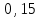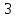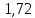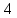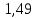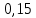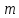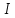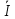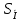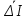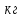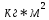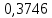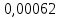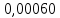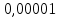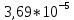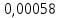Исследование динамики поступательновращательного движения твердого тела
 Скачать 82.31 Kb. Скачать 82.31 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра физики отчет по лабораторной работе №6 по дисциплине «Физика» Тема: «Исследование динамики поступательно-вращательного движения твердого тела»
Санкт-Петербург 2022 Протокол наблюдений Лабораторная работа № 6 «Исследование динамики поступательно- вращательного движения твердого тела»
Выполнил: студент группы 2206 Палей К.А. ____________ Проверил: Попов Ю.И. _____________ Цель работы: Изучение законов поступательно-вращательного движения твердого тела, сохранения энергии, определение момента инерции маятника. Приборы и принадлежности: Маятник Максвелла, секундомер, масштабная линейка, штангенциркуль. Маятник Максвелла (Рисунок 1) представляет собой диск 6, закреп- ленный на стержне 7, подвешенном на бифилярном подвесе 5 к верхнему кронштейну 2. На диск крепится кольцо 8. Верхний кронштейн 2, установленный на вертикальной стойке 1, имеет электромагнит и устройство 4 для регулировки длины бифилярного подвеса. Маятник с кольцом фиксируется в верхнем исходном положении с помощью электромагнита. На вертикальной стойке 1 нанесена миллиметровая шкала, по которой определяется ход маятника. На нижнем кронштейне 3 находится фотоэлектрический датчик 9. Кронштейн обеспечивает возможность перемещения фотодатчика вдоль вертикальной стойки и его фиксирования в любом положении в пределах шкалы 0 - 420 мм. Фотодатчик предназначен для выдачи электрических сигналов на секундомер 10 в момент пересечения светового луча оси фотодатчика диском маятника. 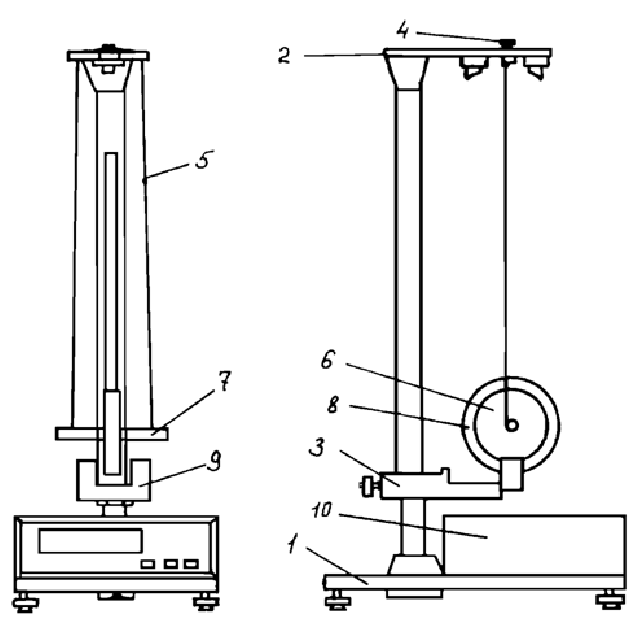 Рисунок 1 Основные теоретические положения: Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу. Маятник Максвелла массой m, поднятый на высоту h путем намотки нитей подвеса на стержень маятника, имеет потенциальную энергию: 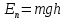 Потенциальная энергия – это скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. После отключения электромагнита маятник начинает раскручиваться, совершая поступательно-вращательное движение. Потенциальная энергия маятника переходит в кинетическую энергию поступательного движения его центра масс: 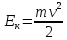 Кинетическая энергия – это скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек. А также в энергию вращательного движения вокруг него: 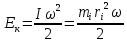 Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением. Закон сохранения механической энергии: Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной. В момент полного разматывания нити происходит рывок маятника и частичный переход механической энергии в тепло. На основании закона сохранения механической энергии на участке пути, меньшем длины нити, можно написать 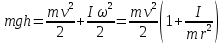 , где 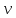 – скорость маятника в момент пересечения оптической оси фотодатчика; ω – его угловая скорость вращения в тот же момент времени, r – радиус стержня, на который намотана нить бифилярного подвеса маятника, I – момент инерции маятника. – скорость маятника в момент пересечения оптической оси фотодатчика; ω – его угловая скорость вращения в тот же момент времени, r – радиус стержня, на который намотана нить бифилярного подвеса маятника, I – момент инерции маятника.Для экспериментального значения момента инерции маятника: 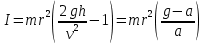 , где учтено, что 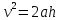 , , 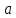 -ускорение, с которым опускается маятник. Учитывая, что -ускорение, с которым опускается маятник. Учитывая, что 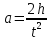 , получим , получим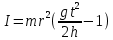 Если учитывать теплоту Q , выделяющуюся маятником в момент рывка нити, то закон сохранения энергии после рывка нити будет иметь вид: 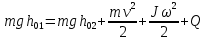 , где высоты 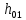 и и 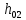 отсчитываются в системе координат, ось высот которой направлена вверх, а начало находится в точке рывка нити. отсчитываются в системе координат, ось высот которой направлена вверх, а начало находится в точке рывка нити.Количество теплоты, выделяющееся при рывке, можно оценить по изменению высоты первого подъёма маятника: 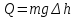 , где 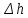 – изменение высоты наивысшего положения маятника в первом цикле спуск – подъём. – изменение высоты наивысшего положения маятника в первом цикле спуск – подъём.Теоретическое значение момента инерции маятника относительно его оси рассчитывается по формуле: 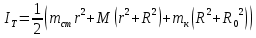 , где 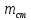 – масса стержня, – масса стержня, 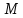 – масса диска, укрепленного на стержне, – масса диска, укрепленного на стержне, 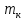 – масса кольца, – масса кольца, 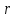 – радиус стержня, – радиус стержня, 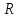 – внешний радиус диска, – внешний радиус диска, 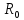 – внешний радиус кольца. – внешний радиус кольца.Обработка результатов:
Проверка на промахи 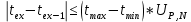 При первом измерении 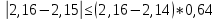 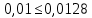 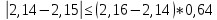 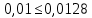 Промахов нет При втором измерении 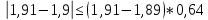 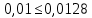 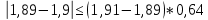 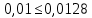 Промахов нет При третьем измерении 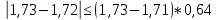 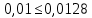 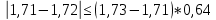 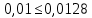 Промахов нет При четвертом измерении 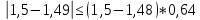 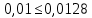 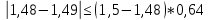 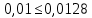 Промахов нет 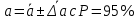
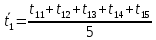 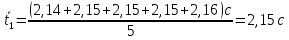 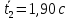 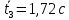 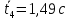 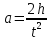 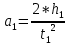 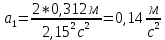 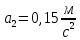 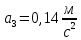 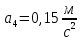 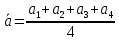 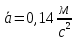 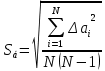 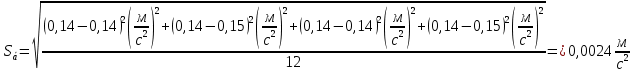 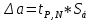 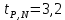 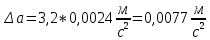 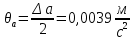 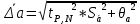 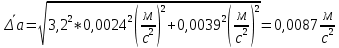 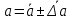 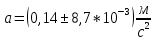 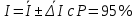
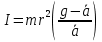 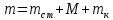 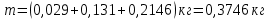 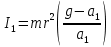 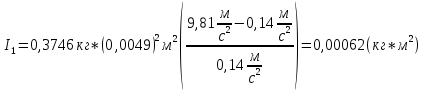 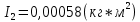 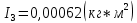 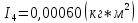 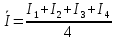 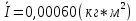 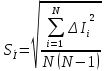 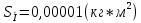 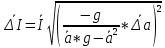 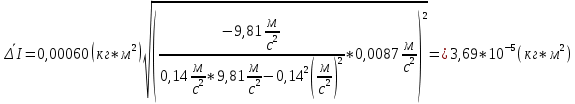 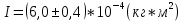 Для одного из опытов рассчитаем величину момента инерции маятника: 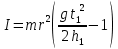 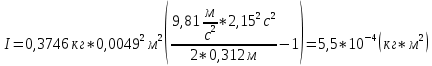 Рассчитаем теоретический момент инерции: 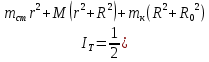 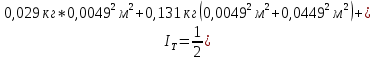 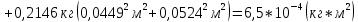 Рассчитаем количество теплоты 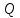 , выделившееся при рывке нити маятника в нижней точке его движения: , выделившееся при рывке нити маятника в нижней точке его движения: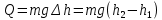 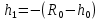 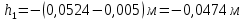 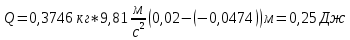 Вывод: В пункте 3 рассчитан экспериментальный момент инерции маятника, равный 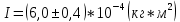 . В пункте 4 для одного из опытов рассчитан момент инерции маятника, равный . В пункте 4 для одного из опытов рассчитан момент инерции маятника, равный 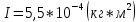 . В пункте 5 рассчитан теоретический момент инерции маятника, равный . В пункте 5 рассчитан теоретический момент инерции маятника, равный 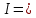 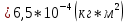 . Результаты получились относительно схожими, поэтому можно сказать, что эксперимент был достаточно точным. . Результаты получились относительно схожими, поэтому можно сказать, что эксперимент был достаточно точным.В пункте 5 рассчитано количество теплоты 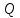 , выделившееся при рывке нити маятника в нижней точке его движения, равное , выделившееся при рывке нити маятника в нижней точке его движения, равное 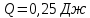 . . |