Измерительный практикум
 Скачать 295 Kb. Скачать 295 Kb.
|
|
ИЗМЕРИТЕЛЬНЫЙ ПРАКТИКУМ При проведении измерений руководствуются общими принципами, которые позволяют выбрать наиболее подходящие методы при их наиболее эффективном использовании. Последнее подразумевает необходимость добиться максимально возможной при данном методе точности и воспроизводимости результатов и устранить характерные для такого методы систематические ошибки. Например, при измерении линейкой возможна ошибка, обусловленная параллаксом, отсчетом нуля, неточностью нанесения делений самой линейкой. Такие ошибки легко устраняются, в частности, во втором случае предмет измеряют по двум отсчетам, а неточность нанесения делений устраняют калибровкой. Выбор метода измерения (на примере измерения длины) В обычных лабораторных условиях речь, как правило, идет о длинах в интервале 10-8 (длина свободного пробега молекул водорода) до 109 м (расстояние от Земли до Солнца), при этом скорость движения предмета v << с, где с – скорость света. Эти измерения проводят опосредованно, и в понятие «длины» вкладывается разный смысл. Поэтому обычно задаются следующими вопросами:
Если проводят измерение цилиндра, то для этих целей достаточно штангенциркуля, причем всегда нужно убеждаться, действительно ли стержень цилиндрический. Микроскопом можно измерить диаметр капилляра, так как его величина не превышает 0,2 мм. Расширить диапазон и повысить точность измерения можно, используя метод оптической интерференции. При малых значениях используют самые различные типы волн – световые, рентгеновские, электронные, нейтронные. Огромные космические расстояния определяют косвенно, например по яркости звезды. Естественные пределы точности измерений. Не только инженеры, но и экономисты, юристы, лингвисты должны иметь понятие о пределах точности измерений. Как бы мы ни были аккуратны в процессе измерений, невозможно провести измерения с любой точностью. Это связано со следующими ограничениями: а) квантовомеханическим принципом неопределенностей. б) случайными флуктуациями измерительных устройств, называемых шумами. Причины случайных флуктуаций:
где d - интервал значений и изменения ЭДС; k – постоянная Больцмана; T – температура. Таким образом, чтобы исключить случайные ЭДС, возникающие в металле, его нужно охладить до Т = 0.
Измерения длин и углов а. Линейный нониус. Линейным нониусом называется линейка В с делениями, скользящая вдоль другой линейки А большего размера, на который нанесена основная шкала (рис, 1). Пусть х – величина одного деления нониуса; Y- величина одного деления основной шкалы; m – полное число делений нониуса. 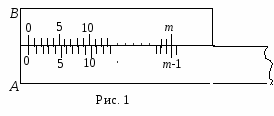 Деления нониуса наносят так, чтобы эти m делений укладывались в (m – 1) (или в 2m – 1 … или в общем случае в сm – 1) делениях основной шкалы. Таким образом: mx = (m – 1) y (1) или mx = (cm – 1) y, (1) или иначе говоря, величина деления нониуса х всегда на В  первом случае х на 1/10 меньше y, а во втором случае х на 1/10 меньше 2y. первом случае х на 1/10 меньше y, а во втором случае х на 1/10 меньше 2y.Если нониус на или Итак, точностью нониуса А называется величина разности между делением масштаба и делением нониуса (или между целым числом делений масштаба и делением нониуса) y/ m. Иначе, точность нониуса есть отношение цены деления масштаба (y) к числу делений нониуса (m). Р 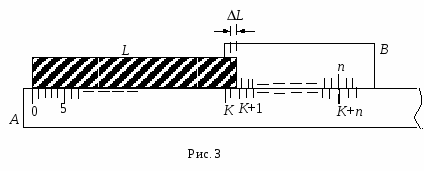 ассмотрим измерение длины с помощью линейного нониуса. Пусть измеряется длина ассмотрим измерение длины с помощью линейного нониуса. Пусть измеряется длина где меньше одного деления основной шкалы. Подвинем теперь к стержню нониус так, чтобы ноль нониуса совпал со вторым концом стержня. При этом какое-нибудь n-е деление нониуса будет ближе других совпадать с соответствующим делением масштаба, т.к. деления нониусам не равны делениям основной шкалы. (На основной шкале это будет (К + n)-е деление при С = 1). Как видно из рис. 3 но Итак, длина отрезка (в нашем случае), измеряемого с помощью нониуса, равна целому числу делений масштаба, укладывающихся в измеряемой длине, плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба. б. Круговой нониус. К 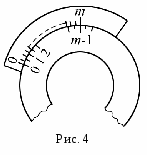 руговым нониусом называется дуговая линейка с делениями, скользящая вдоль круга, разделенного на градусы или более мелкие, угловые деления (рис. 4). Принципиально этот нониус, предназначенный для измерения углов, ничем не отличается от линейного. Если деление лимба составляет градусов (или минут), а деление нониуса градусов, то в соответствии с уравнением (1) руговым нониусом называется дуговая линейка с делениями, скользящая вдоль круга, разделенного на градусы или более мелкие, угловые деления (рис. 4). Принципиально этот нониус, предназначенный для измерения углов, ничем не отличается от линейного. Если деление лимба составляет градусов (или минут), а деление нониуса градусов, то в соответствии с уравнением (1)m = (m – 1), где m – по-прежнему число делений нониуса. Точность кругового нониуса = / m. О 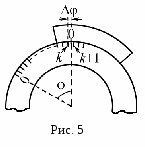 тсчет измеряемого угла ведется следующим образом. Допустим, начальное положение какого-либо прибора (например, зрительной трубы спектроскопа), связанного с механизмом, поворачивающим нониус, соответствует совпадению нуля нониуса с нулем лимба. При повороте этого прибора на угол (рис. 5) ноль нониуса оказывался между k и (k + 1) делениями лимба, а n-е деление нониуса совпало с каким-либо делением лимба; в соответствии с уравнением (3) угол поворота тсчет измеряемого угла ведется следующим образом. Допустим, начальное положение какого-либо прибора (например, зрительной трубы спектроскопа), связанного с механизмом, поворачивающим нониус, соответствует совпадению нуля нониуса с нулем лимба. При повороте этого прибора на угол (рис. 5) ноль нониуса оказывался между k и (k + 1) делениями лимба, а n-е деление нониуса совпало с каким-либо делением лимба; в соответствии с уравнением (3) угол поворота Первое положение прибора на нуле лимба аналогично положению первого конца стержня, которое измеряется с помощью линейного нониуса, а второе положение прибора – положению второго конца стержня, с которым совмещен ноль линейного нониуса. Часто при пользовании приборами, снабженными лимбом и круговым нониусом, приходится измерять углы в обоих направлениях (по часовой стрелке и против нее). Поэтому во многих случаях круговые нониусы состоят из двух совершенно одинаковых шкал, расположенных по обе стороны ноля. При измерении углов необходимо пользоваться той шкалой, которая идет по направлению отсчета. в. Конический нониус (микрометрический винт). М 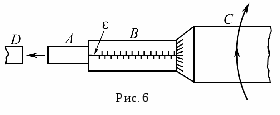 икроскопический винт является частью прибора, называемого микрометром. Микрометр предназначен, чаще всего, для измерения малых длин: например, диаметра стержня проволоки, толщины пластинки и т.п. Кроме того, микроскопический винт применяется в других приборах. Например, измерительный микроскоп снабжен микрометрическим винтом, позволяющим отсчитывать высоту подъема или опускания объектива. На рис. 6 изображен микроскопический винт. На стержне винта А укреплено устройство, называемое барабаном С, внутри которого и находится собственно винт. Основная линейная шкала нанесена на втулке В, а нониус на конической части барабана. При вращении барабана по часовой стрелке (рис. 6), стержень А смещается влево. В микрометре при нулевом положении стержень А касается упора D. Вращая барабан против часовой стрелки, сдвигают стержень А вправо, а затем зажимают измеряемую деталь между упором и стержнем. Таким образом, смещение стержня до упора определяет размер детали. (В микроскопе микрометрический винт находится в вертикальном положении, и перемещение стержня А соответствует перемещению объектива микроскопа). Ход винта соответствует одному делению основной шкалы, которое мы опять назовем y. Нониус, нанесенный на коническую поверхность, содержит m делений. В микроскопическом винте нониус перпендикулярен основной шкале, поэтому деление нониуса не может совпадать с делением основной шкалы, как это было для линейного и кругового нониуса. Совпадение нуля нониуса с нулем или каким-либо делением основной шкалы заменяется здесь (в микрометрическом винте) совпадением нуля конического нониуса с продольной риской Е, проведенной по всей длине втулки. При полном обороте винта нониуса, а с ним и стержень А смещается на одно деление основной шкалы, и его нуль опять совпадает с риской. Нониус содержит m делений, следовательно, при повороте винта на 1/m часть полного оборота первое деление оборота нониуса совпадает с риской, а стержень переместится при этом на 1/m часть деления основной шкалы (на (1/m)y). Ясно, что совпадение n-го деления нониуса с риской говорит о перемещении стержня на n(y / m). Таким образом, и здесь точность нониуса (y / m). Измеряемая длина определяется смещением стержня от нулевого положения Задание 1. Измерить углы на гониометре Гониометр – прибор, применяемый в оптике для измерения углов отклонения лучей света. Он снабжен оптическими трубами, одна из которых, фиксирующая направление луча, связана с дуговым (круговым) нониусом, скользящим по лимбу. По шкале лимба и нониусу отсчитывается положение этой трубы. Цель работы, которую Вы сейчас выполняете, – научиться делать отсчет с помощью кругового нониуса. Поэтому Вам дан гониометр, лишенный оптических стекол. Им, конечно, нельзя произвести точное измерение, но можно научиться делать отсчет углов. Ход работы
Задание 2. Измерить период колебаний крестообразного маятника секундомером Измеряется время падения груза, висящего на нити с определенной высоты. Нить наматывается на валик крестообразного маятника. Вращение креста и разматывание нити задерживают, установив положение груза на высоте консоли (подставки, на которой расположен прибор), а затем, освободив крест, пускают секундомер. Ход работы
Задание 3. Измерить линейные размеры тела микрометром и штангенциркулем; ознакомиться с методами расчета погрешностей Ход работы
При вычислениях рекомендуется оставлять значащих цифр на одну больше, чем содержится в измеренных выражениях (например, а, b и с могут быть длиной, шириной и высотой параллелепипеда). Или а = H – длина цилиндра; b = D – диаметр цилиндра; V – объем измеряемого тела.
6. Определите среднеквадратичную погрешность результата серии измерений по формуле 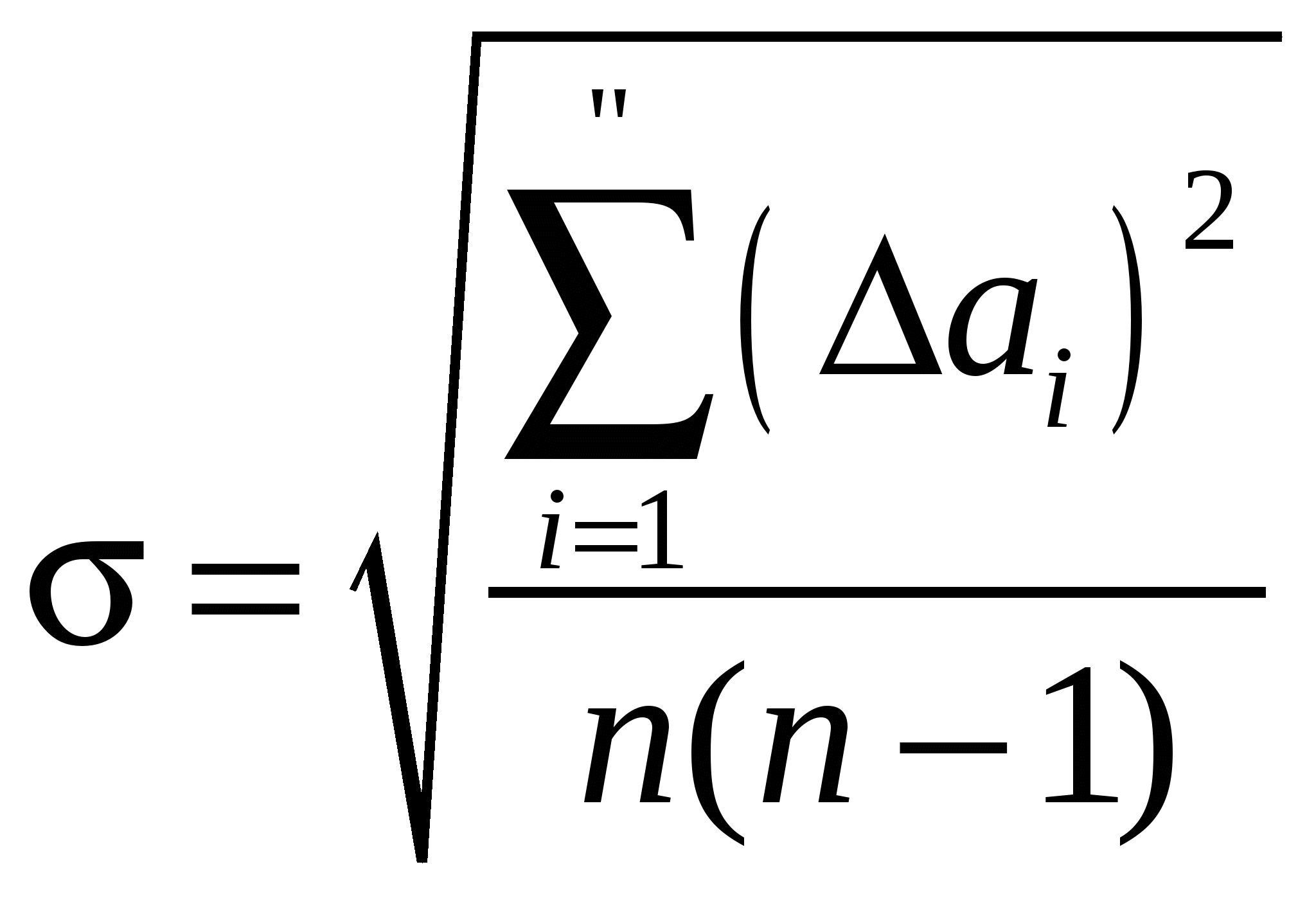 , где n – число измерений. , где n – число измерений.
7. Из таблицы коэффициентов Стьюдента найдите коэффициент tn, где надежность = 0,95; n – число произведенных измерений. tn =………………… 8. Оцените границы доверительного интервала, то есть абсолютную погрешность серии измерений по формуле а с.н. = tnа =………… bс.и. = tnb=………… bс.и. = tnc=………… 9. Определите погрешность одного измерения хо.и. = = …, где – надежность (или доверительная вероятность), равная 0,95; – половина цены наименьшего деления прибора. ао.и = … ; bо.и = … ; cо.и = … . 10. Рассчитайте суммарную погрешность прямых измерений 11. Запишите окончательный результат в виде (в соответствии с правилами округления цифровых значений) а а = ……… b b = ……… c c = ……… 12. Оцените относительную погрешность: а = (а/<a>)100 % = ……….. о = (b/<b>)100 % = ……….. c= (c/<c>)100 % = ………… 2. Погрешность косвенных измерений
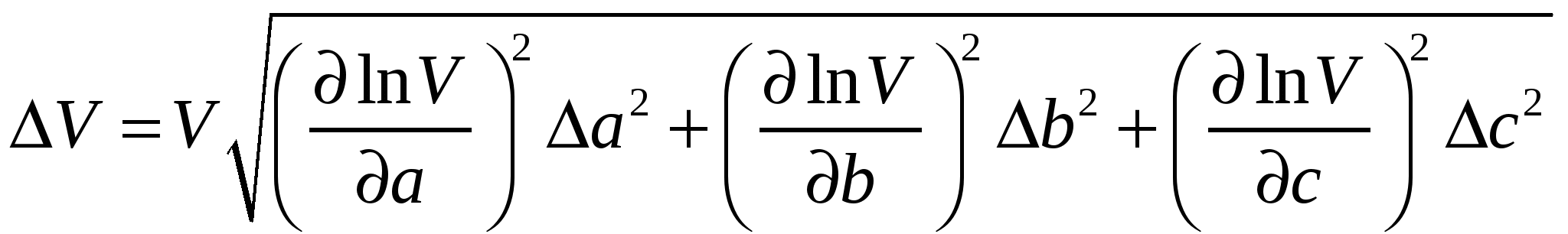 2. а = b= c = (из п.10) 3. 4. Абсолютная погрешность V = ……………………………….
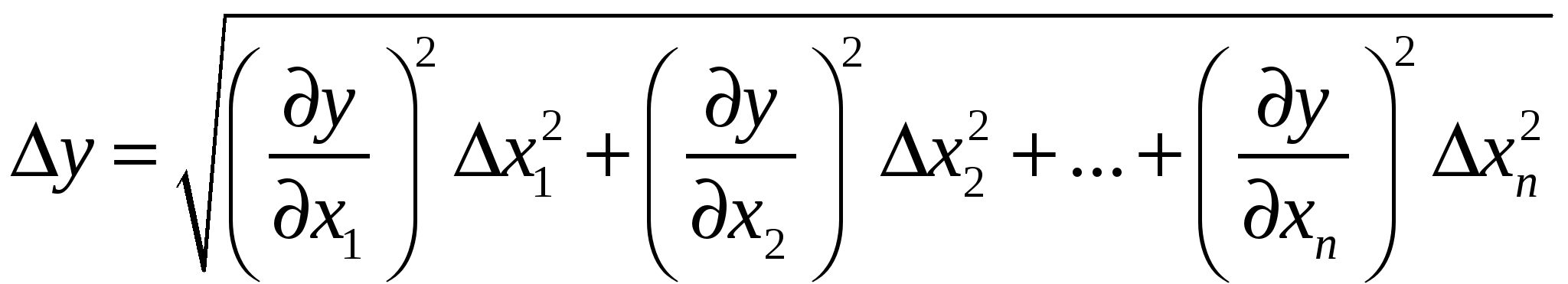 , ,где х1, х2, х3 – погрешности прямых измерений; КОНТРОЛЬНЫЕ ВОПРОСЫ
16. y = a / (a + b); y – ? 17. y = a (a + b); y ? 18. y = a2+b2 ; y ? 19. y = (a sin a) / (b a); y ? 20. 21. y = tg a y ? 22. y = a + b y ? 23. y = a b y ? 24. y = a2 + b2 y ? 25. y = a2 b2 y ? ОБЩИЕ ВОПРОСЫ И ЗАДАНИЯ ДЛЯ ИНДИВИДУАЛЬНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО ТЕМЕ «ИЗМЕРИТЕЛЬНЫЙ ПРАКТИКУМ»
|
