Задача 3 (динамика). Дано рисунок 3
 Скачать 207.5 Kb. Скачать 207.5 Kb.
|
|
Задача 3 Вариант 31 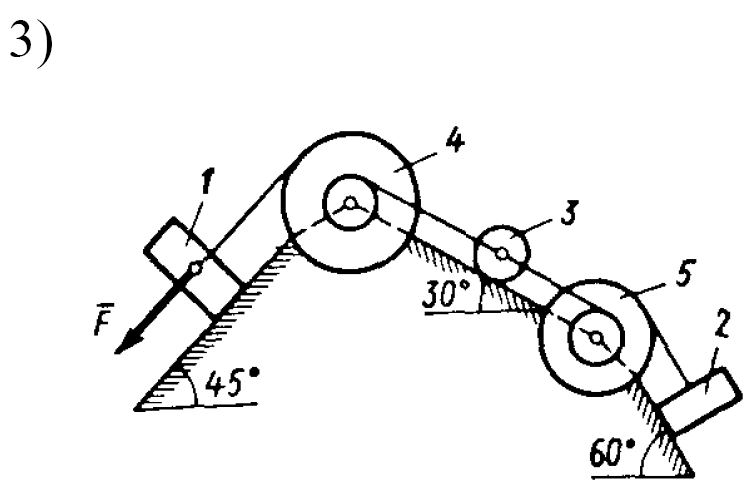 Дано: рисунок 3; R4=0.3 м; r4=0.1 м; R5=0.2 м; r5=0.1 м; m1=6 кг; m2=0; m3=2 кг; m4=0; m5=8 кг; М4=0.6 Нм; f=0.1; F=20(5+2s); s1=1.2 м. Найти: ω5. Механическая система состоит из грузов 1 и 2 (коэффициент трения скольжения грузов о плоскость f=0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R4=0,3 м, r4=0,1 м, R5=0,2 м, r5=0,1 м (массу каждого шкива считать распределенной по его внешнему ободу). Тела системы соединены друг с другом нерастяжимыми нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Под действием постоянной силы F система приводится в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивления, равные соответственно М4 и М5. Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы F равно s1. Решение: 1. Система имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение груза 3, полагая, что груз движется по направлению силы F. Составим уравнение Лагранжа 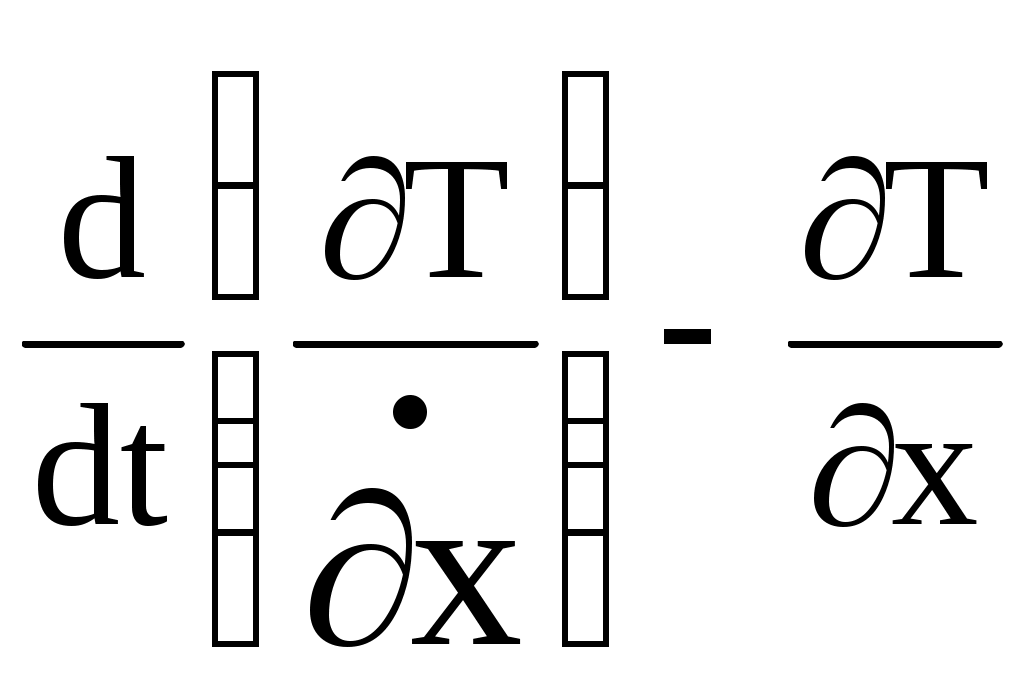 =Q. =Q.2. Определим кинетическую энергию Т системы, равную сумме энергий всех тел: Т=Т1+Т2+Т3+Т4+Т5. Скорости выразим через угловую скорость шкива 5 – ω5. Соотношения скоростей определятся как 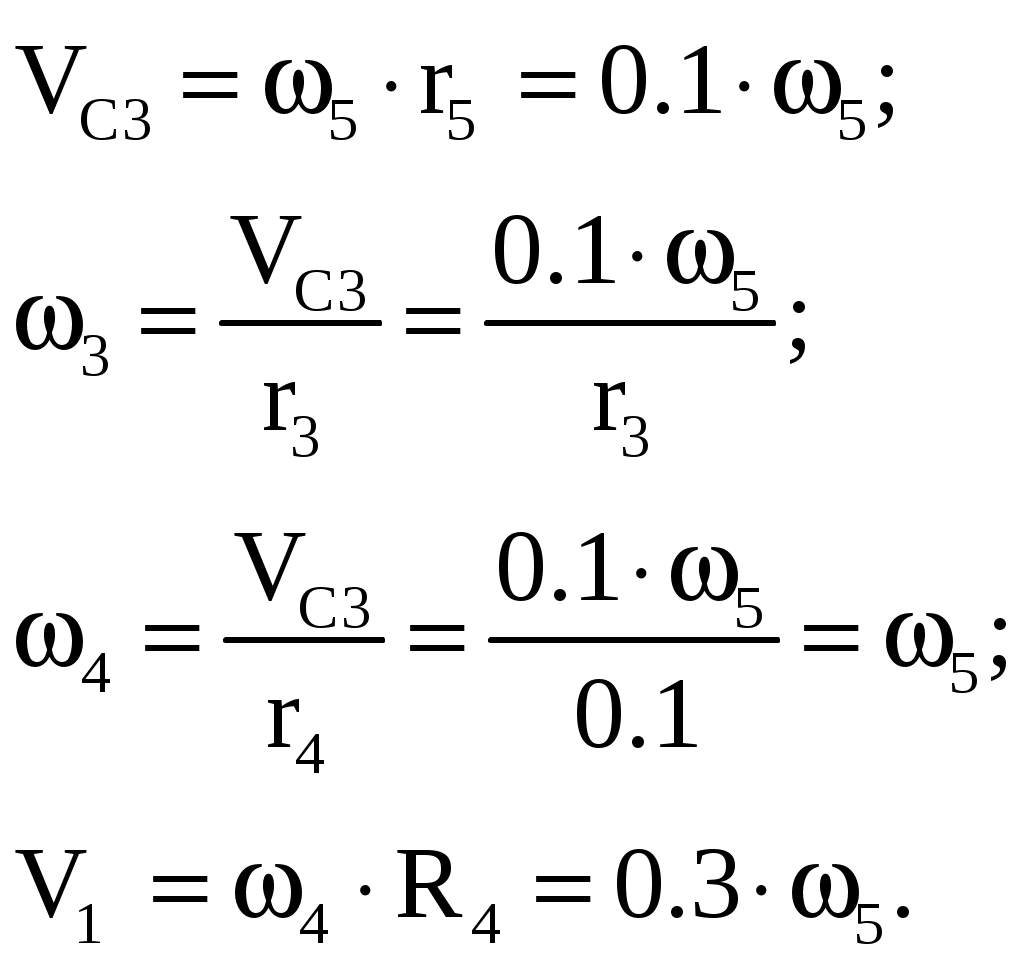 Для груза 1: Для груза 2: T2=0 так как масса груза равна нулю. Для груза 3: учтем, что 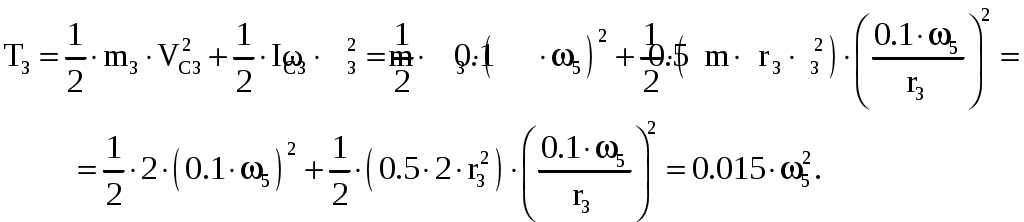 Для груза 4: T4=0 так как масса груза равна нулю. Для груза 5: учтем, что Сумма кинетических энергий всех тел системы составит 3. Найдем обобщенную силу Q. Вычислим работу элементарных сил и момента через перемещения системы. Получим Выразим перемещения через x. 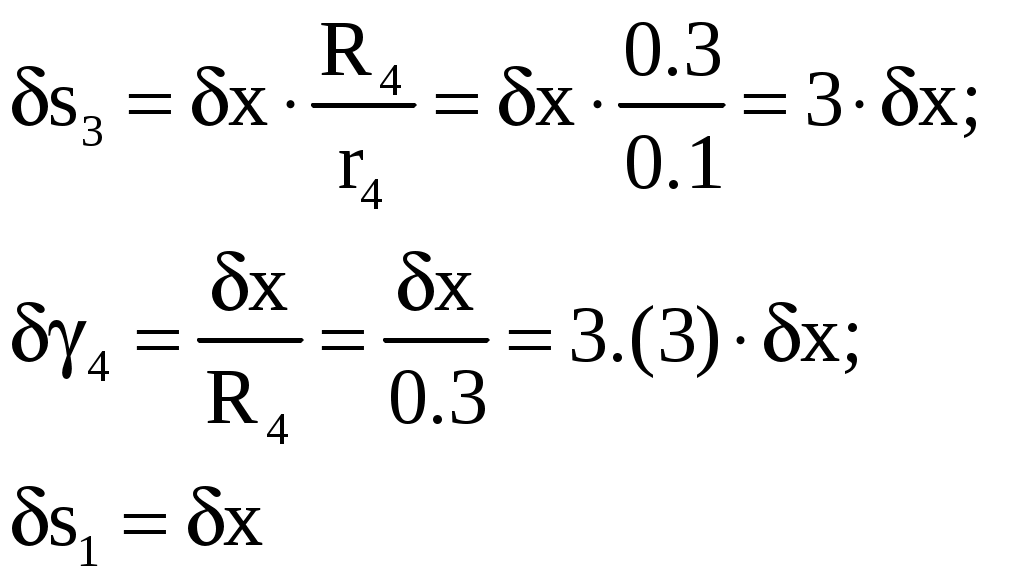 . .Подставляя полученные значения в равенство и преобразуя найдем, что Коэффициент x и будет обобщенной силой Q. Следовательно, учтя, что P=mg, где g=9.8 м/с2, получим 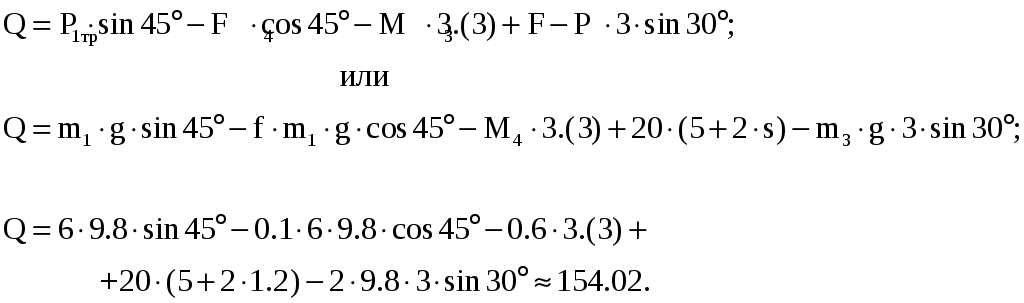 6. Подставляя в полученное выше уравнение Лагранжа имеем 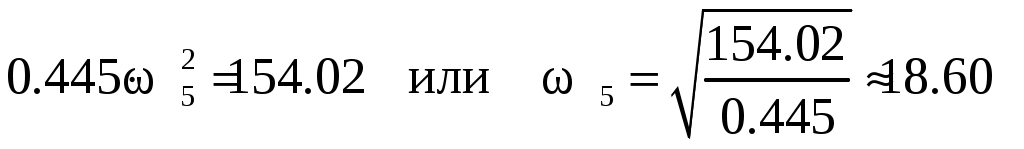 с1. с1.Ответ: 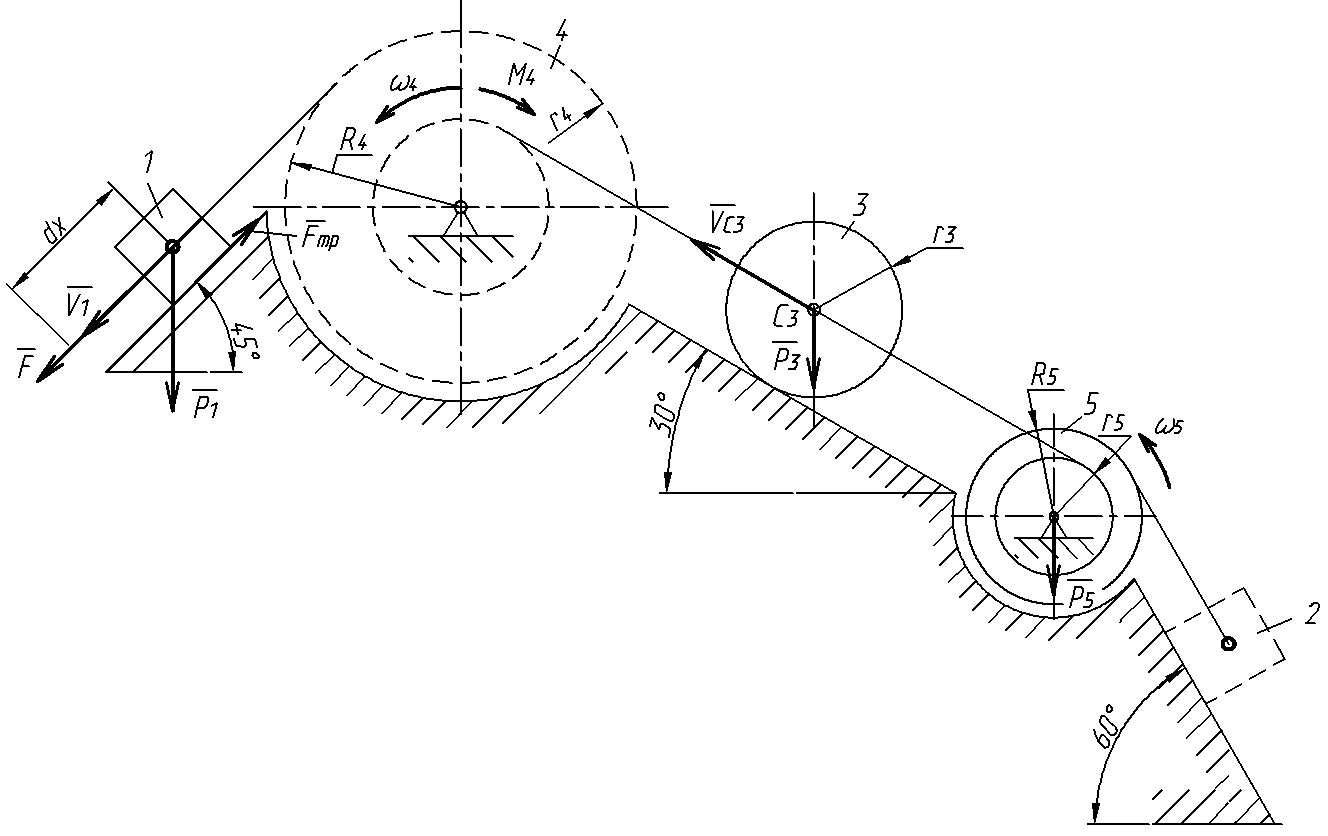 |
