работа. T mkv

• Название: T mkv
• Анкор: работа
• Дата: 04.05.2021
• Размер: 165.5 Kb.
• Имя файла: 52-55.docx
• Тип: Документы; #201308

Вопрос 52

Кинетической энергией механической системы называется сумма кинетических энергий всех точек этой системы:

T = ∑m_kv_k²/2,

где m_k и v_k — масса и скорость k-й материальной точки, принадлежащей данной системе.


На основании теоремы Кёнига кинетическая энергия произвольной механической системы определяется по формуле

T = Mv_C²/2 + ∑ m_kv_kr²/2

где M — масса всей системы;
v_C — скорость центра масс системы;
m_k — масса k-й точки системы;
v_kr — относительная скорость k-й точки при движении её вокруг центра масс (т.е. v_k=v_C +v_kr).

Из этой формулы можно получить следующие частные случаи для твёрдого тела:

при поступательном движении тела

vk= vC , vkr=0,

T = mvC2/2;

при вращении тела вокруг оси, проходящей через его центр масс,

vC=0 , vkr= ω × rk ,

T = ∑ mkvkr2/2 = Jω2/2,

где J — момент инерции тела относительно оси, проходящей в данный момент времени через центр масс;

ω — угловая скорость вращения тела;

в случае произвольного движения тела (например при плоскопараллельном движении)

T = mvC2/2 + Jω2/2.

Вопрос 53

Теорема об изменении кинетической энергии: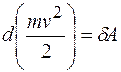

.

Интегральная (конечная) форма. Теорема об изменении кинетической энергии материальной точки: изменение кинетической энергии мате­риальной точки на некотором ее перемещении равно алгебраической сумме работ всех действующих на эту точку сил на том же перемещении.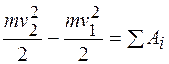



Теорема об изменении кинетической энергии механической системы формулируется: изменение кинетической энергии меха­нической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении:

.

В случае неизменяемой системы сумма работ внутренних сил на любом перемещении равна нулю ( )

Вопрос №54
Закон сохранения механической энергии. При движении механической системы под действием сил, имеющих потенциал, изменения кинетической энергии системы определяются зависимостями:

, откуда  ,

т.е.

.

Сумму кинетической и потенциальной энергий системы называют полной механической энергией системы

Таким образом, при движении механической системы в стационар­ном потенциальном поле полная механическая энергия системы при движении остается неизменной.



Вопрос №55

Ударом называется механическое взаимодействие материальных тел, приводящая к значительным изменениям скорости их точек за очень малый промежуток времени, который называется временем удара. Например: удар меча о стену, где время удара составляет доли секунды, но происходит изменение скорости меча.
В элементарной теории удара, время удара считается бесконечно малым, то есть происходит мгновенно (скачкообразно) изменение скорости.
Перемещении точек системы, так же бесконечно малые, таким образом точки системы в процессе удара не перемещаются, необходимо рассчитать два процесса: соударение происходящая мгновенно и дальнейшее (пример, погружение гвоздя вместе с молотком не относящаяся к самому удару).
В процессе удара у точек системы имеется бесконечно большие ускорения, то есть на них действуют бесконечно большие силы, но при ударе так же могут быть силы которые приводят к разрушению.
График реальной силы при ударе.

Где: τ- время удара, Fmax – максимальная ударная сила. τ -> 0 , Fmax -> 0 .
2. Ударная сила.
Бесконечно большая сила действующая на месте соударения тел называется ударным, а те силы, которые в процессе удара остаются конечными (сила тяжести) называется ударным.
Описание явления удара построена на основе соответствующих теорем в интегральной форме, в частности в теореме об изменении количества движения.
Q - Q0 = ∑ Skl (1).
Для одной точке получивший удар имеет следующий вид:
mU – mU0 = S (2).
Где S – импульс равнодействующей.
S всех сил приложенных к точке за все время удара τ:
S = (3).
Модуль которого геометрический представляет площадь графика (рис.1).
а) Если сила в процессе удара конечная не ударная, а время мала то импульс силы будет бесконечной малой.
б) Если сила будет бесконечной большой (ударной), тогда, несмотря на то, что время мала, импульс силы будет величиной конечной.
Таким образом сделаем вывод о том, что при ударе не ударные силы можно не учитывать. Изменение скоростей будет определяться только импульсами ударных сил.
Sуд = – ударный импульс (4).