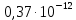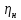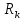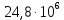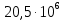Курсовая. ПГД-К-19. Дать сравнительную оценку приближенных методов решения задач теории упругого режима фильтрации нефти
 Скачать 233.79 Kb. Скачать 233.79 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ НЕФТИ И ГАЗА ИМ М. С. ГУЦЕРИЕВА Кафедра разработки и эксплуатации нефтяных и газовых месторождений Курсовая работа по дисциплине: «Подземная гидромеханика» на тему: «Дать сравнительную оценку приближенных методов решения задач теории упругого режима фильтрации нефти» Вариант №19 Выполнил Проверил Борхович С. Ю Доцент к.т.н Ижевск, 2022 СОДЕРЖАНИЕ Введение…………………………………………………………………………...3 Теоретическая часть…………………………………………………………..4 Точное решение осесимметричного притока нефти к скважине ………4 Приближенные методы решения задач упругого режима фильтрации нефти………………………………………………………………………11 Расчетная часть………………………………………………………………14 Рассчитать депрессию на пласт по точной формуле и по приближенным формулам …………………………………….................15 2.2. Найти относительную погрешность расчетов ………………………...16 Выводы…………………………………………………………………………...17 Список использованной литературы…………………………………………...18 ВВЕДЕНИЕ Постановка и решение газогидродинамических задач разработки месторождений в значительной степени определяются природой движущих сил, обеспечивающих фильтрацию нефти и газа в пласте. В связи с этим важное значение имеет значение режимов нефтегазоносных пластов. Режим продуктивных пластов в процессе их разработки зависит как от многих естественных факторов, так и от системы разработки. К естественным факторам, влияющим на режим разрабатываемого пласта, относятся геологические особенности строения пласта, фильтрационные характеристики пород пласта и насыщающих его жидкостей и газов, физические условия в пласте – давление, температура и т.д. Режимом нефтегазоводоносного пласта называется проявление доминирующей формы пластовой энергии в процессе разработки залежи нефти и газа. При пуске скважины в эксплуатацию в условиях упругого режима движение жидкости к скважине начинается за счет использования потенциальной энергии упругой деформации пласта и жидкости сначала в ближайшей окрестности забоя, затем во все более удаленных областях пласта. Характерная особенность проявления упругого режима в процессе разработки нефтяных месторождений – длительность процесса перераспределения пластового давления после начала работы скважины или изменения темпа отбора жидкости из скважины. Это связано с тем, что при фильтрации вязкой жидкости в пласте возникают очень большие силы сопротивления. Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта, и тем медленнее, чем больше вязкость жидкости и коэффициенты объемной упругости жидкости и пласта ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Точное решение осесимметричного притока нефти к скважине Были предложены различные способы линеаризации уравнения. Если рассматривается плоскорадиальный приток к скважине, то, как известно из теории установившейся фильтрации нефти воронка депрессии очень крутая, и в большей части пласта давление мало отличается от контурного. На этом основании Леибензон предложил заменить переменное давление p в коэффициенте уравнения на постоянное давление pк, равное начальному давлению в пласте. Тогда, обозначив 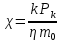 получим уравнение получим уравнение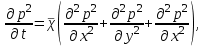 (1) (1)которое является линейным уравнением пьезопроводности относительно функции р2, где χ - константа, аналогичная коэффициенту пьезопроводности. Такой способ линеаризации, когда переменный коэффициент χ в уравнении при различных значениях давления принимается константой, называется линеаризацией по Лей6ензону. В дальнейшем различными авторами были предложены уточнения к линеаризации по Лейбензону. Так. И. А. Чарный предложил свести уравнение к линейному заменой переменного давления в коэффициенте на значение 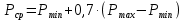 где pmах и pmin - максимальное и минимальное давления в газовой залежи на расчетный период. Используем линеаризованное уравнение (1) для решения конкретной задачи о притоке газа в скважину бесконечно малого радиуса (точечный сток), расположенную в бесконечно протяженном пласте с постоянной толщиной h. В начальный момент времени пласт невозмущен, т.е. давление во всем пласте постоянно и равно pk. С этого момента начинается отбор газа с постоянным дебитом Qат. Нужно найти изменение давления по пласту с течением времени p(r, t). Для плоскорадиальной фильтрации газа (1) запишется следующим образом: 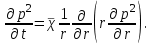 (2) (2)Проинтегрировав уравнение (2) при начальном условии p2 = pk2 при t =0, 0 < r < ∞ (3) и при граничном условии в удаленных точках р2 = рk2 при r = ∞, t > 0. (4) Выведем условие для давления на забое скважины. Записав выражение для массового дебита исходя из закона Дарси в дифференциальной форме для плоскорадиальной фильтрации: 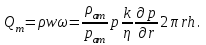 И использовав равенства 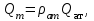 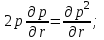 а так же сократив на рат, получим: 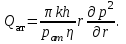 Из этого соотношения можно выразить условие на стенке газовой скважины бесконечно малого радиуса: 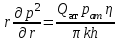 при r = 0. (5) при r = 0. (5)Таким образом, для решения поставленной задачи уравнение (2) должно быть проинтегрировано при условиях (3), (4), и (5). Полученные выражения для совершенного газа аналогичны соотношениям для упругой жидкости, только давление входит в квадрате: 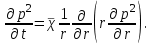 p2 = pk2 при t = 0, 0 < r < ∞ р2 = рk2 при r = ∞, t > 0 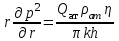 при r = 0 при r = 0Решение лиеаризованного уравнения Лейбензона для газа получим по основной формуле упругого режима для упругой жидкости с учетом 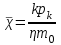 для газа и коэффициента для газа и коэффициента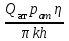 , аналогичных коэффициенту пьезопроводности и коэффициенту , аналогичных коэффициенту пьезопроводности и коэффициенту 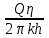 для жидкости: для жидкости: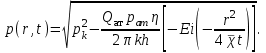 (6) (6)Для малых значений аргумента 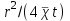 в соответствии можно заменить интегральную показательную функцию логарифмической в соответствии можно заменить интегральную показательную функцию логарифмической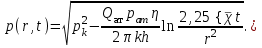 (7) (7)Решения (6)-(7) являются приближенными, так как получены в результате интегрирования линеаризованного уравнения (1), а не точного. Формулы (6) и (7) определяют (при фиксированных значениях времени t распределение давления вокруг газовой скважины, работающей с постоянным дебитом с момента t = 0. Эти депрессионные кривые имеют такой же характер, как при установившейся фильтрации очень крутые вблизи скважины (рис.1,а). Если задать значение r можно найти изменение давления в данной точке с течением времени. Можно найти изменение давления на забое (при r = rc) после начала работы скважины (рис.1,б): 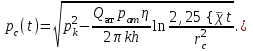 (8) (8)Кривые распределения давления по пласту при неустановившемся притоке газа к скважине в разные моменты времени (а) и динамика давлений в фиксированных точках пласта (б)  а p pк 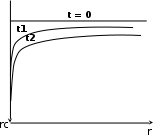 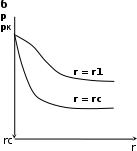 Рис. 1 Г.И. Баренблатт, применяя анализ размерностей, показал, что нелинейное уравнение Лейбензона при определенных начальных и граничных условиях имеет точное решение, которое может служить эталоном для сравнения с ним приближенных решений. Для его получения рассматривается задача о нестационарном плоскорадиальном притоке газа с постоянным дебитом к скважине в бесконечном пласте. Необходимо проинтегрировать нелинейное уравнение Лейбензона 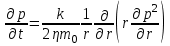 (9) (9)При начальных граничных условиях p2 = pk2 при t = 0, 0 < r < ∞ р2 = рk2 при r = ∞, t > 0. 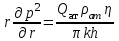 при r = 0 при r = 0Г.И. Баренблаттом показано, что в такой постановке давление зависит от некоторого единого комплекса, включающего в себя обе переменные – r и t, а дифференциальное уравнение в частных производных приводится к обыкновенному дифференциальному уравнению, которое легко интегрируется. Чтобы установить, от каких аргументов будет зависеть давление, проведем анализ размерностей. Распределение давления в пласте зависит, как следует из постановки задачи, от пяти определяющих параметров (n=5): r, t, pk, k/(2ηm0), Qатpатη/(πkh). Среди этих параметров - три с независимыми размерностями: r, t, pk (k=3). Как следует из П-теоремы, искомая функция – давление, приведенное к безразмерному виду F=p/pk, , будет зависеть от двух безразмерных комплексов (n-k = 5-3 = 2). Такими безразмерными комплексами являются следующие: 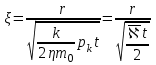 и и 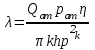 , ,т.е. F=p/pk=F(ξ,λ). Дифференцируя функцию F по t и по r как сложную функцию и подставляя производные в уравнение (9), получим, что функция F удовлетворяет обыкновенному дифференциальному уравнению 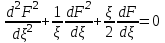 (10) (10)при этом начальные и граничные условия сводятся к следующим: 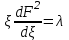 при ξ=0; F(ξ,λ)=1 при ξ=∞ (11) при ξ=0; F(ξ,λ)=1 при ξ=∞ (11)Уравнение (10) при условиях (11) было проинтегрировано численно. Результаты расчетов приведены в табл.1 для значений λ=0,01 и λ=0,004994. Через ξ* в табл.1 обозначено такое значение аргумента ξ, что для ξ < ξ* значения ξdF2/dξ, отличаются от λ меньше, чем на 0,01%. Значит, для ξ < ξ* можно считать, что ξdF2/dξ = λ. Проинтегрировав это равенство, получим: F2=F2(ξ*, λ) + λln(ξ/ ξ*) F(ξ, λ) = [F2 (ξ*, λ)- λln(ξ*/ξ)]½ для ξ< ξ*. Поэтому значения F(ξ, λ) для ξ< ξ* в табл. 1 не приведены. Таблица 1 - Результаты численного расчета автомодельного решения
1.2 Приближенные методы решения задач упругого режима фильтрации нефти Решение задачи о притоке нефти к скважине методом последовательной смены стационарных состояний Для определения изменения дебита скважины после пуска её в эксплуатацию воспользуемся приближенным методом последовательной смены стационарных состояний, согласно которому в каждый момент времени вся область движения жидкости условно разделяется на две области: возмущенную и невозмущенную. В возмущенной области, начинающейся от стенки скважины, давление распределяется так, как будто бы движение жидкости в ней установившееся. Внешняя граница этой области служит в данный момент контуром питания и определяется в соответствии с приведенным радиусом влияния . В невозмущенной области пласта давление постоянно и соответствует начальному давлению. Итак, дебит в соответствии с формулой Дюпюи с течением времени при плоскорадиальном притоке упругой жидкости к скважине будет изменяться по следующей зависимости: 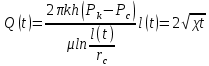 Коэффициент пьезопроводности определяется по следующей формуле: 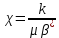 Метод усреднения Еще одним приближенным методом, применительно к задачам неустановившейся фильтрации нефти, является метод усреднения временной производной по пространству. В качестве примера рассматривается прямолинейно-параллельная фильтрация нефти. Соответствующее этому случаю точное дифференциальное уравнение имеет вид 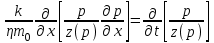 (12) (12)Допущением является то, что коэффициент сверхсжимаемости z(р) можно заменить на 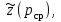 где pср - некоторое среднее давление в области фильтрации. Введем обозначение р1=р/z(р). Тогда уравнение примет вид где pср - некоторое среднее давление в области фильтрации. Введем обозначение р1=р/z(р). Тогда уравнение примет вид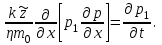 (13) (13)Пусть имеется первоначально невозмущенный газонасыщенный пласт шириной В, толщиной h, длиной L. С трех сторон пласт ограничен непроницаемыми поверхностями, а с четвертой стороны (х = 0) вскрыт галереей. В момент t = 0 через галерею начинает отбираться нефть с постоянным массовым дебитом, который в соответствии с законом Дарси можно записать в виде: 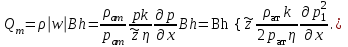 Требуется определить давление в пласте в любой момент времени t > 0. Для этого нужно найти решение уравнения (13) в области изменения  удовлетворяющее начальному и граничным условиям: удовлетворяющее начальному и граничным условиям:p1 = p10 при t = 0 (40) 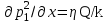 при x=0, где при x=0, где 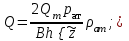 (14) (14)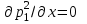 при x = L (15) при x = L (15)Как и в методе последовательной смены стационарных состояний принимаем, что в каждый момент времени существует конечная возмущенная область l(t), на границе которой выполняются условия p12=p102, 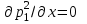 при x = l(t) (16) при x = l(t) (16)Центральным моментом в рассматриваемом методе усреднения является принятие условия 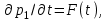 РАСЧЕТНАЯ ЧАСТЬ
2.1 Рассчитать депрессию на пласт по точной формуле и по приближенным формулам 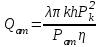 Подставив наши данные, получим: 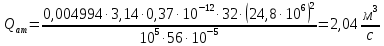 определим коэффициент 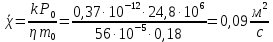 Точное решение Определим безразмерную величину ξ для r = rc 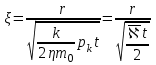 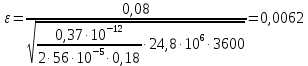 Сравнивая полученное значение ξ со значениями в таблице 1 для λ=0,004994 заключаем, что ξ < ξ* поэтому безразмерное давление F определим по формуле 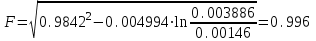 . .Выразив давление P = Pc, получим Pc= FPk = ּ 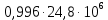 = 24,7ּ Па = 24,7ּ ПаДепрессия на пласт через 1 час будет равна: ∆P = Pk-Pc = (24,8-24,7)ּ106 = 0,1 МПа. Расчет методом последовательной смены стационарных состояний 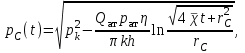 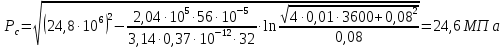 Депрессия будет равна: ∆ P = (24,8-24,6)ּ106 = 0,2 МПа. 2.2 Относительная погрешность расчетов 1. Расчет по линеаризованной формуле: 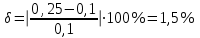 2. Расчет методом последовательной смены стационарных состояний: 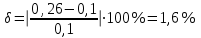 ВЫВОД Линеаризованная формула эффективна только в тех случаях, когда радиус скважины очень маленький, потому что в этом случае воронка депрессии очень крутая и давление по всему пласту в целом не сильно отличается от начального. Но при больших радиусах скважины эта формула будет давать большую погрешность, т.к. давление по пласту будет сильно отличаться от начального. В отличие от линеаризованной формулы, формула последовательной смены стационарных состояний эффективна для любых радиусов скважин, но только для первой фазы движения, т.е. пока воронка депрессии не достигнет радиуса контура. Как показали расчеты наиболее точной является линеаризованная формула. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебник для вузов. - Москва-Ижевск: Институт компьютерных исследований, 2003. - 480 с. Басниев К.С. и др. Подземная гидромеханика. М.: Недра, 1993 г., 172-179 с. Басниев К.С. и др. Подземная гидромеханика. М.:Недра, 1993 г., 131-151 с., 159-171 с. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебное пособие для вузов. - М. - Ижевск: Институт компьютерных исследований, 2005, 544 с. Подземная гидромеханика: Учебно-методическое пособие / сост. С.Ю. Борхович, И.В. Пчельников, С.Б. Колесова – Ижевск: Издательский центр « Удмуртский университет» 2017 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 103
103