Давление абсолютное, избыточное, атмосферное, вакуумное. Абсолютное давление

• Название: Давление абсолютное, избыточное, атмосферное, вакуумное. Абсолютное давление
• Дата: 27.02.2019
• Размер: 137.78 Kb.
• Имя файла: tt.docx
• Тип: Документы; #69052

1. 
   Давление: абсолютное, избыточное, атмосферное, вакуумное.
   

Абсолютное давление отсчитывается от абсолютного нуля. В этой системе атмосферное давление. Следовательно, абсолютное давление равно

Р абс= Р атм + Р изб

Абсолютное давление всегда является величиной положительной.

Избыточное давление  отсчитывается от атмосферного давления, т.е. от условного нуля. Чтобы перейти от абсолютного к избыточному давлению необходимо вычесть из абсолютного давления атмосферное, которое в приближенных расчетах можно принять равным 1ат:

Р изб = Р абс – Р атм.

Иногда избыточное давление называют манометрическим.

Вакуумметрическим давлением или вакуумом называется недостаток давления до атмосферного

Р вак = Р атм – Р абс (отрицательное).

Избыточное давление показывает либо избыток над атмосферным, либо недостаток до атмосферного. Ясно, что вакуум может быть представлен как отрицательное избыточное давление

.

Атмосферное давление – Гидростатическое давление, оказываемое атмосферой на все находящиеся в ней предметы. А. д. — существенная характеристика состояния атмосферы; в каждой точке атмосферы оно определяется весом вышележащего воздуха.
Нормальное атмосферное – 760 мм.ртст, при 0 цельсия

2. 
   Первый закон термодинамики, математическая формулировка
   

Вечный двигатель первого рода невозможен, т. е. невозможно построить машину, которая совершала бы механическую работу, не затрачивая на это соответствующего количества энергии (Оствальд)

Изменение внутренней энергии системы ΔU может происходить за счет обмена теплотой Q и работой А с окружающей средой. В термодинамике условились считать положительными величинами теплоту, полученную системой, и работу, совершенную системой.

Тогда из формулировки первого закона термодинамики следует, что теплота, полученная системой извне, расходуется на приращение внутренней энергии и работу, совершенную системой, т. е.

_{Q = ΔU+W.}

Если эти количества бесконечно малы, то закон записывается в дифференциальной форме:

,

где dU- полный дифференциал внутренней энергии системы; δQ и δW - бесконечно малые количества теплоты и работы.

3. 
   Второй закон термодинамики
   

Формулировка Кельвина и Планка Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

Формулировка Клаузиуса Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.

Теплота в работу вся переходит не может!

Вечного двигателя 2 рода быть не может!

4. 
   Внутрення энергия, энтропия, энтальпия.
   

Внутренняя энергияU является функцией состояния для процессов при постоянном объеме и энтропии. Она не изменяет свое значение при возвращении системы в исходное состояние независимо от пути перехода. Это кинетическая энергия поступательного, вращательного движения, потенциалная энергия частиц тела.

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении.

Определением этой величины служит тождество: H=U+PV

Размерность энтальпии-Дж/моль.

Основное содержание второго начала термодинамики заключается в постулировании существования функции, называемой энтропией S, которая для обратимых процессов определяется по уравнению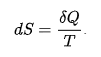

5. 
   Графический анализ термодинамических процессов, его частных случаев на PV и TS диаграммах
   

Термодинамический процесс (тепловой процесс) – изменение макроскопического состояния термодинамической системы. Если разница между начальным и конечным состояниями системы бесконечно мала, то такой процесс называют элементарным (инфинитезимальным).

Система, в которой идёт тепловой процесс, называется рабочим телом.

Изобарный процесс p = const, V/T = const

Изобарным называется процесс, протекающий при постоянном давлении p= const. Из уравнения состояния идеального газа слуедует:

v/T=R/p=const

или

 v₂/v₁=T₂/T₁,

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

l=p(v₂ – v₁).

Т. к. pv₁=RT₁иpv₂=RT₂, то

l=R(T₂ – T₁).

Количество теплоты при c_p= const определяется по формуле:

q=c_p(T₂ – T₁).

Изменение энтропии будет равно: 

s₂ – s₁= Δs = c_pln(T₂/T₁).



Изохорный процесс V = const, p/T = const

При изохорном процессе выполняется условие v= const.

Из уравнения состояния идеального газа (pv=RT) следует:

 p/T=R/v= const,

т. е. давление газа прямо пропорционально его абсолютной температуре:

 p₂/p₁=T₂/T₁.

Работа расширения в изохорном процессе равна нулю (l= 0), так как объем рабочего тела не меняется (Δv= const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v= const определяется по формуле:

q=c_v(T₂ —  T₁). 

Т. к.l= 0, то на основании первого закона термодинамики Δu=q, а значит изменение внутренней энергии можно определить по формуле:

Δu=c_v(T₂ — T₁).

Изменение энтропии в изохорном процессе определяется по формуле:

s₂ – s₁= Δs = c_vln(p₂/p₁) = c_vln(T₂/T₁).



Изотермический процесс T = const, pV = const

При изотермическом процессе температура рабочего тела остается постоянной T= const, следовательно:

pv = RT = const

или

p₂/p₁=v₁/v₂,

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

l=RTln (v₂ – v₁) =RTln (p₁ – p₂).

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu= 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

q=l.

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

s₂ – s₁= Δs=Rln(p₁/p₂) =Rln(v₂/v₁).



Адиабатный процесс

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой.

Так как dq= 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

du+pdv= 0

или

Δu+l= 0,

следовательно

Δu= —l. 

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq= 0 выразим следующим образом:

dq=c_адdT= 0.

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад= 0).

Известно, что

с_p/c_v =k

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

pv^k= const.

6. 
   Теплоемкость газов. Массовая и объемная теплоемкость. Взаимосвязь.
   

Если к рабочему телу в каком-либо процессе подвести теплоту или отвести от него теплоту, то это приведет к изменению его температуры.

Отношение количества теплоты подведенной к рабочему телу (или отведенной от рабочего тела) в данном процессе к изменению его температуры называется теплоемкостью тела (системы тел):

[Дж/К], (4.1)

где dQ - элементарное количество теплоты; dT- элементарное изменение температуры.

Количество теплоты, подведенное к рабочему телу (или отведенное от рабочего тела) в каком-либо процессе х, для изменения его температуры на определенное количество градусов зависит от количества рабочего тела. В зависимости от количественной единицы рабочего тела, к которому подводится теплота, в термодинамике различают массовую /удельную/, объемную и мольную теплоемкости

Удельная /массовая/ теплоемкость с_х - это теплоемкость, отнесенная к единице массы рабочего тела:

[Дж/кгК]. (4.2)

Объемная теплоемкость c'_х - это теплоемкость, отнесенная к единице объема рабочего тела при нормальных физических условиях (Р = 101325 Па и Т= 273,15 К):

[Дж/м³К]. (4.3)

Мольная теплоемкость c_x - это теплоемкость, отнесенная к количеству рабочего тела в молях:

[Дж/кмольК] (4.4)

где n - количество газа в молях.

Между указанными теплоемкостями существует следующая связь:

, (4.5)

где v₀ - удельный объем при нормальных физических условиях;- молярная масса.

Изменение температуры рабочего тела при одном и том же количестве сообщаемой теплоты зависит от процесса, в котором подводится теплота, поэтому теплоемкость является функцией процесса. Т.е. одно и то же рабочее тело в зависимости от процесса требует для своего нагрева на один градус различное количество теплоты. Численно величина с изменяется от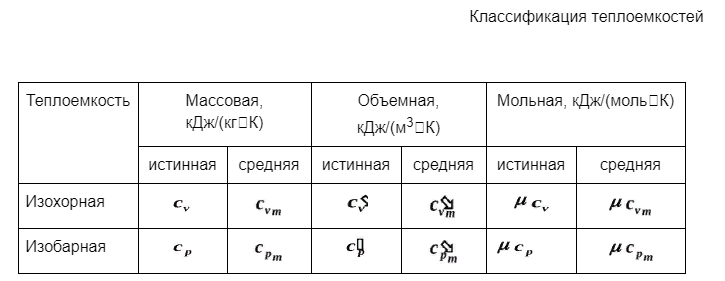до.

7. 
   Политропный процесс. Частные случаи, графическое изображение. Уравнение политропы.
   

Политропным называется процесс, в котором удельная теплоёмкость газа остаётся постоянной, т.е. c = const.

Уравнение политропного процесса (политропы): pvⁿ= const (3.3)

где коэффициент n = называется показателем политропы.

Теплоёмкость в политропном процессе c = c_v 

Политропный процесс есть обобщенный случай всех рассмотренных выше изопроцессов:

при n = 0 p = const – изобарный процесс;

при n = 1 pv = const – изотермический процесс;

при n = k pv^к = const – адиабатный процесс;

при n =  v = const – изохорный процесс.



.