курсовая по сопромату. курсовая Тренин. Деформация и прочность балок при плоском изгибе
 Скачать 67.24 Kb.
|
КУРСОВАЯ РАБОТА на тему
САНКТ-ПЕТЕРБУРГ 2021г. «Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова» (БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова») УТВЕРЖДАЮ:
З А Д А Н И Е
Студент ___________________ ___________________ подпись ФИО дата Руководитель ________________ __Храмова Д. А.__ __ подпись ФИО дата Содержание Введение…………………………………………………………………………. 3 Теоретическая часть…………………………………………………………….. 5 Решение………………………………………………………………………….. 8 Заключение……………………………………………………………………… 12 Список использованной литературы………………………………………….. 14 Введение Сопротивление материалов – наука о прочности, жесткости и надежности элементов инженерных конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые, как говорят, надежные размеры деталей машин, различных конструкций и сооружений. В процессе эксплуатации машин и сооружений их элементы (стержни, балки, болты, заклепки и т.д.) в той или иной степени участвуют в работе конструкции и подвергаются действию различных сил – нагрузок. Для обеспечения нормальной работы конструкции инженеру необходимо так подобрать материал и размеры элементов конструкции, чтобы они: • не разрушались, т.е. были прочными; • были достаточно жесткими, т.е. перемещения (деформации) элементов конструкции не превышали заданных величин; • были устойчивыми, т.е. сохраняли под действием нагрузок первоначальную устойчивую форму равновесия. Сопротивление материалов – наука о прочности, жесткости и устойчивости элементов конструкций и сооружений. Прочность – способность конструкции и ее элементов сопротивляться разрушению под действием внешних нагрузок. Жесткость – способность конструкции и ее элементов сопротивляться нагрузкам в их стремлении изменить форму и размеры тела. Устойчивость – способность конструкции и ее элементов сохранять форму упругого равновесия под действием внешних нагрузок. Сопротивление материалов является наукой экспериментально - теоретической, так как широко использует опытные данные и теоретические исследования. Зарождение науки о сопротивлении материалов связано с именами Леонардо да Винчи и Галилео Галилея. Значительный вклад в развитие науки о сопротивлении материалов сделан выдающимися учеными Бернулли, Сен-Венаном, Коши, Ламе и др., которые сформулировали основные допущения и дали некоторые расчетные уравнения. Изгибом называют такое напряжённо-деформированное бруса, при котором его продольная ось искривляется. Детали машин и элементы конструкций, имеющие форму стержней и работающие на изгиб, называют сельскохозяйственном машиностроении к балкам относят разнообразные рычаги, оси, зубья борон, рессоры, балансирные брусья, части рам и т.п. Плоскость действия внешних нагрузок называют силовой плоскостью. Линию пересечения силовой плоскости с плоскостью поперечного сечения называют силовой линией. Прямолинейная балка имеет как минимум две главных плоскости. Главной плоскостью балки называется плоскость, которая проходит через одну из главных центральных осей инерции сечения и продольную ось балки. Изгиб, при котором в поперечном сечении балки под действием внешних нагрузок возникает только изгибающий момент, называют чистым изгибом. а) контуры поперечных сечений остаются плоскими, т.е. поперечные линии останутся прямыми и в деформированном состоянии, но повернутся на угол; б) продольные линии, в том числе и ось балки, искривляются по дуге окружности. Верхние линии укорачиваются, а нижние удлиняются; в) углы деформирующихся элементов (квадратиков) остаются при чистом изгибе прямыми, поэтому сдвиг и связанные с ним касательные напряжения как в поперечных, так и в продольных сечениях отсутствуют; г) изменение размеров поперечного сечения, т.е. поперечная деформация, происходит так: ширина балки вверху увеличивается (в зоне сжатия), а внизу уменьшается в растянутой области. Теоретическая часть Балка изгибается сосредоточенной силой F. Используя метод мысленных сечений и составляя уравнения равновесия для отсеченных частей балки, определим внутренние усилия. При определении внутренних усилий будем придерживаться следующего правила знаков: 1) поперечная сила Qy считается положительной, если она стремится повернуть рассматриваемый элемент балки по часовой стрелке; 2) изгибающий момент Мz считается положительным, если при изгибе элемента балки верхние волокна элемента оказываются сжатыми, а нижние – растянутыми (правило зонта). Таким образом, решение задачи по определению внутренних усилий при изгибе будем выстраивать по следующему плану: 1) на первом этапе, рассматривая условия равновесия конструкции в целом, определяем, если это необходимо, неизвестные реакции опор (отметим, что для консольной балки реакции в заделке можно и не находить, если рассматривать балку со свободного конца); 2) на втором этапе выделяем характерные участки балки, принимая за границы участков точки приложения сил, точки изменения формы или размеров балки, точки закрепления балки; 3) на третьем этапе определяем внутренние усилия в сечениях балки, рассматривая условия равновесия элементов балки на каждом из участков. Итак, Решение задачи на изгиб предполагает определение реакций. Для этого размещаем оси координатной системы  , в левом крайнем сечении балки, ось всегда направлена и совпадает с её продольной осью. Затем, рисуем вектор в заделке A, направив его по осям. Истинное направление векторов устанавливается после решения уравнений статики. Для определения реакций в системе координат XYZ приведем распределенную нагрузку q к сосредоточенной силе 2qa которая приложена к центру тяжести площади прямоугольника длиной 2a и высотой q. Запись MAiZ означает, что ищется сумма моментов MAiZ от сил, вращающих тело относительно оси Z, проходящей через точку А. Положительным считается направление вращения правого буравчика (с правой нарезкой) пре-образующее вращательное движение в поступательное по положительному направлению оси +Z. После того, как реакции опор будут найдены, сами опоры можно будет исключить из задачи, заменив их влияние найденными реакциями. Уравнения равновесия имеют вид: 1) сумма сил, действующих на балку, на вертикальную ось Y; 2) сумма моментов всех сил относительно опоры А. При этом в качестве положительного направления момента принято направление поворота балки (как твердого тела) против часовой стрелки относительно опоры А (ось Z на нас). Количество участков: n=3 , их нумерация произвольна. (Границей участков называется резкое изменение любых параметров балки при движении поперечного сечения вдоль ее продольной линии). Применяя метод сечений, Проводя в произвольном сечении x мысленное отсечение участка, для 1-го участка получим расчетную схему. Внутренние усилия направляем в положительном направлении осей этой системы координат. К отсеченному кусочку прикладываем все действующие на него внешние силы. Повторяем эту процедуру для каждого участка. Чертим эпюры, согласно расчетам. 1) В точках действия сосредоточенных сил на эпюре Q будут скачки на величину этих сил, а на эпюре М будут изломы; 2) В точках действия сосредоточенных моментов на эпюре М будут скачки на величину этих моментов, а на эпюре Q никаких изменений не будет; 3)На участках действия распределённой нагрузки q(х) = const эпюра Q будет наклонной прямой, а эпюра М - параболой. Выпуклость параболы направлена навстречу действию распределённой нагрузки. Вершина параболы будет в точке, где эпюра Q переходит через ноль. Выполняем по правилам проверку эпюр. Условие прочности (максимальные напряжения не превышают допускаемые ) имеет вид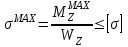 
Интегрируя первый раз, дифференциальное уравнение упругой линии балки 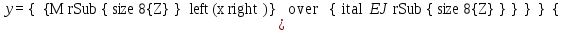 по координате x, распространяющейся на всю длину балки, получим уравнение углов поворота  ее сечений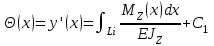 . (а)Интегрируя второй, получим уравнение прогибов 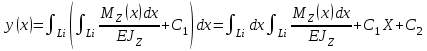 (б). Постоянные интегрирования С1 и С2 определяются из граничных условий рассматриваемой балки. Особенности решения покажем на конкретном примере. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, 
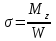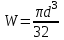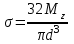
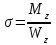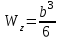или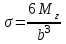 
, 
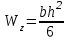или 
или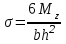 
(b, h – см. рис.3.8)