Лабораторная работа 3. Лабораторная 3. Детерминированные циклические вычислительные процессы с управлением по аргументу. Частичное интегрирование
 Скачать 313.62 Kb. Скачать 313.62 Kb.
|
|
Лабораторная работа №3 Тема: «Детерминированные циклические вычислительные процессы с управлением по аргументу. Частичное интегрирование» Цель работы: Разработать алгоритм вычисления определенного интеграла с помощью детерминированного вычислительного процесса с управлением по аргументу Используемое оборудование: персональный компьютер, компилятор «Pascal ABC» 4. Задача 1. Написать программу для вычисления определенного интеграла из индивидуального задания методом прямоугольника левых частей. Протестировать программу на определенном интеграле, вычисленным в ходе выполнения самостоятельной работы 3 5. Математическая модель 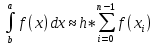 6. Блок-схема 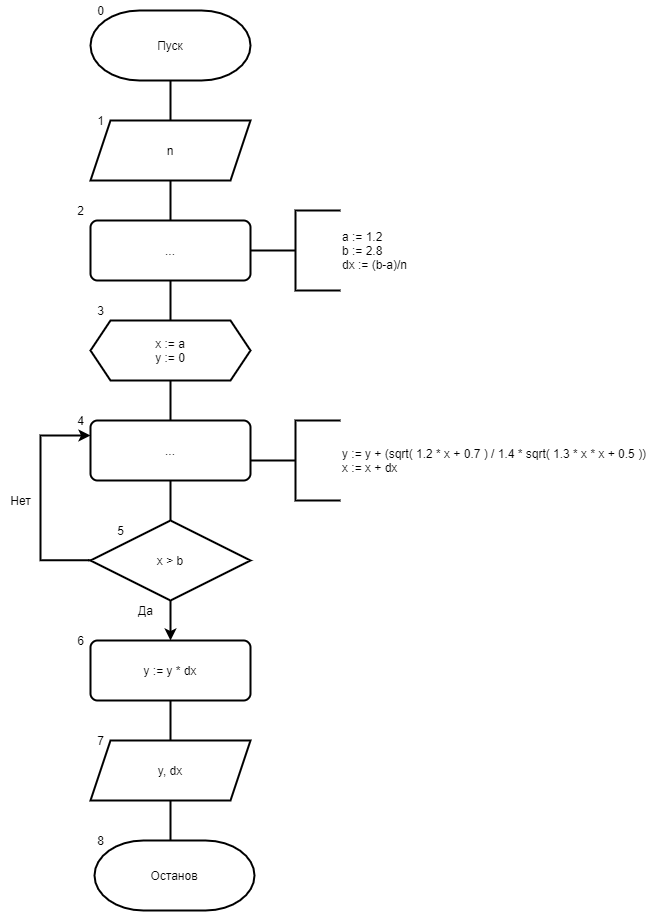 7. Список идентификаторов
8. Код программы Program pr_lev; var a, b, x, y, dx: real; n : integer; begin writeln('Введите кол-во разбиений: '); readln(n); a := 1.2; b := 2.8; dx := (b-a)/n; y := 0; x := a; while x < b do begin y := y + (sqrt(1.2*x+0.7)/1.4*x+sqrt(1.3*x*x+0.5)); x := x + dx; end; y := y*dx; writeln('Значение интеграла, рассчитанное по формуле прямоугольника левых частей: ', y); writeln('Шаг = ', dx) end. 9. Результаты выполненной работы     4. Задача 2. Написать программу для вычисления определенного интеграла из индивидуального задания методом прямоугольника правых частей. Протестировать программу на определенном интеграле, вычисленным в ходе выполнения самостоятельной работы 3 5. Математическая модель 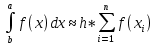 6. Блок-схема 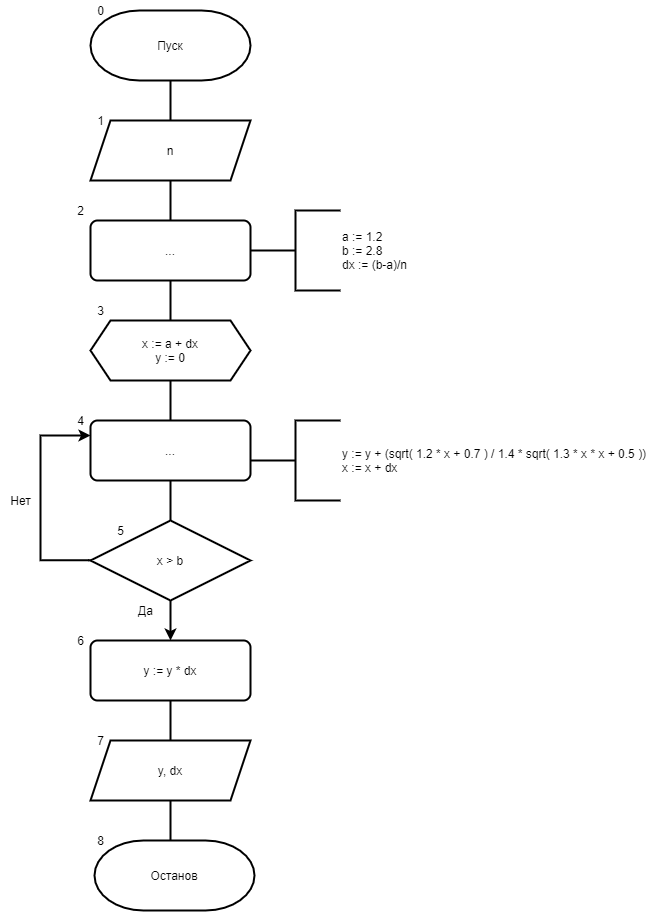 7. Список идентификаторов
8. Код программы Program pr_prav; var a, b, x, y, dx: real; n : integer; begin writeln('Введите кол-во разбиений: '); readln(n); a := 1.2; b := 2.8; dx := (b-a)/n; y := 0; x := a + dx; while x < b do begin y := y + (sqrt(1.2*x+0.7)/1.4*x+sqrt(1.3*x*x+0.5)); x := x + dx; end; y := y*dx; writeln('Значение интеграла, рассчитанное по формуле прямоугольников правых частей: ', y); writeln('Шаг = ', dx) end. 9. Результаты выполненной работы 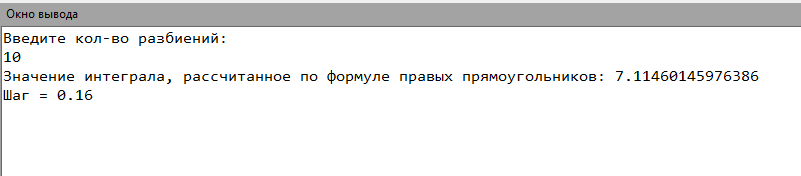    4. Задача 3. Написать программу для вычисления определенного интеграла из индивидуального задания методом трапеций. Протестировать программу на определенном интеграле, вычисленным в ходе выполнения самостоятельной работы 3 5. Математическая модель 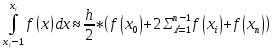 6. Блок-схема 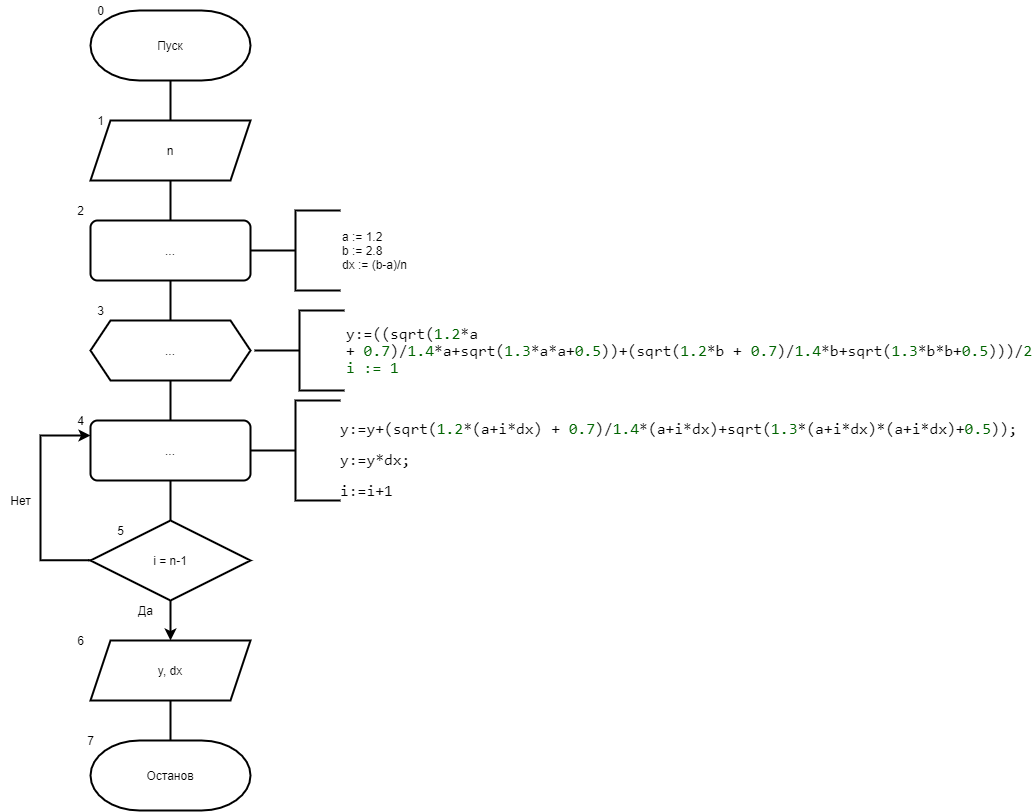 7. Список идентификаторов
8. Код программы Program pr_1; var a,b,dx,y:real; n,i:integer; begin writeln('Введите кол-во разбиений'); readln(n); a := 1.2; b := 2.8; dx := (b - a)/n; y:=((sqrt(1.2*a + 0.7)/1.4*a+sqrt(1.3*a*a+0.5))+(sqrt(1.2*b + 0.7)/1.4*b+sqrt(1.3*b*b+0.5)))/2; for i:=1 to n-1 do y:=y+(sqrt(1.2*(a+i*dx) + 0.7)/1.4*(a+i*dx)+sqrt(1.3*(a+i*dx)*(a+i*dx)+0.5)); y:=y*dx; writeln('Шаг = ',dx); writeln('Y = ',y); end. 9. Результаты выполненной работы     4. Задача 4. Написать программу для вычисления определенного интеграла из индивидуального задания методом парабол. Протестировать программу на определенном интеграле, вычисленным в ходе выполнения самостоятельной работы 3 5. Математическая модель 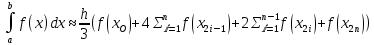 6. Блок-схема 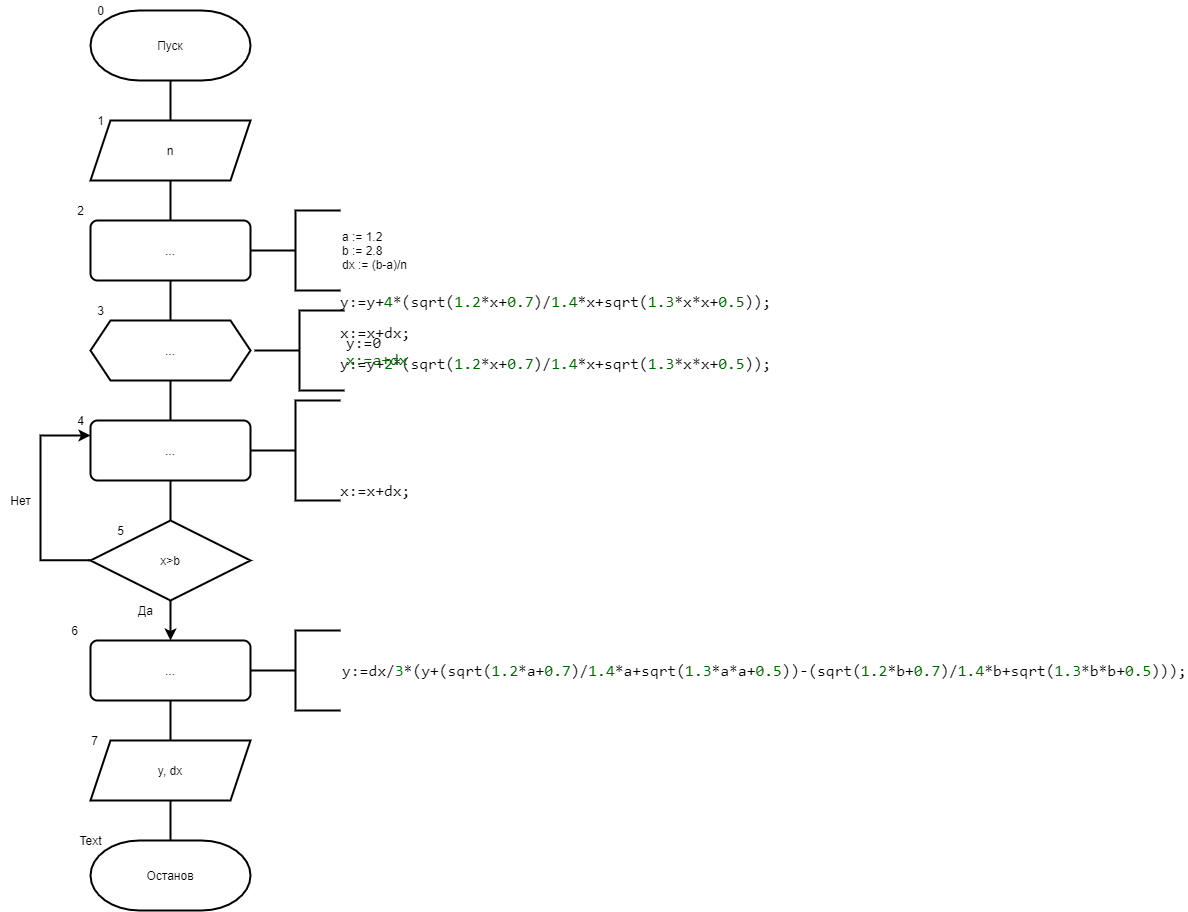 7. Список идентификаторов
8. Код программы program Simpson; var x,a,b,dx,y:real; n:integer; begin a := 1.2; b := 2.8; write('На сколько частей нужно разделить отрезок? n='); read(n); dx:=(b-a)/n; y:=0; x:=a+dx; while xdo begin y:=y+4*(sqrt(1.2*x+0.7)/1.4*x+sqrt(1.3*x*x+0.5)); x:=x+dx; y:=y+2*(sqrt(1.2*x+0.7)/1.4*x+sqrt(1.3*x*x+0.5)); x:=x+dx; end; y:=dx/3*(y+(sqrt(1.2*a+0.7)/1.4*a+sqrt(1.3*a*a+0.5))-(sqrt(1.2*b+0.7)/1.4*b+sqrt(1.3*b*b+0.5))); writeln('Интеграл = ',y); end. 9. Результаты выполненной работы 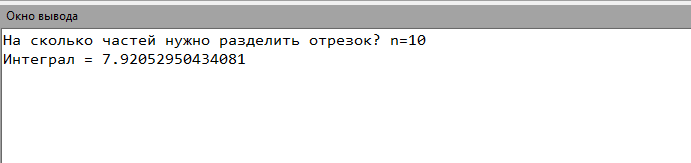 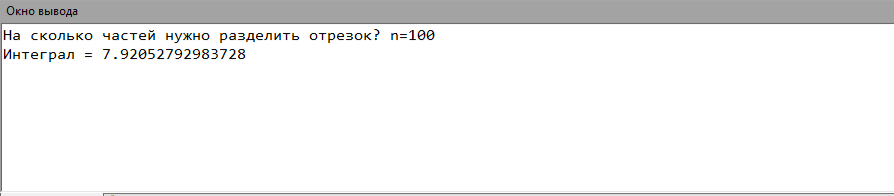 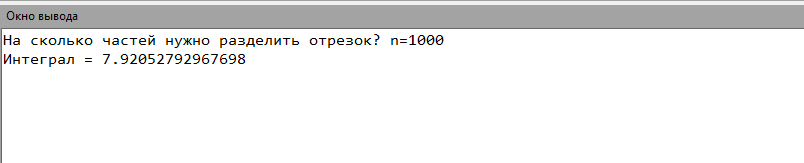 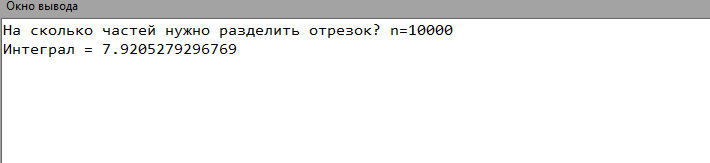 10. Анализ результатов вычислений
11. В ходе решения задач был разработан алгоритм вычисления определенного интеграла с помощью детерминированного вычислительного процесса с управлением по аргументу |
