КН. КР 2 заочное. Программа дисциплины математика
 Скачать 109 Kb. Скачать 109 Kb.
|
|
Информация помещена на сайт ИИТ БГУИР и эл. ящики групп 23.02.2015 г. Программа дисциплины «математика» для заочной формы обучения (II семестр) Раздел 10. Определенный интеграл Тема 10.1. Определенный интеграл и его вычисление. Определенный интеграл, его геометрический и физический смыслы. Основные свойства определенного интеграла. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Тема 10.2. Приложения определенного интеграла. Геометрические и физические приложения определенного интеграла. Тема 10.3. Несобственный интеграл. Несобственный интеграл 1-го рода. Признаки сходимости. Абсолютная и условная сходимость. Раздел 11. Дифференциальные уравнения Тема 11.1. Дифференциальные уравнения первого порядка. Дифференциальные уравнения, основные понятия. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения. Линейные дифференциальные уравнения первого порядка. Тема 11.2. Дифференциальные уравнения высшего порядка. Дифференциальные уравнения высших порядков, допускающие понижение порядка. Линейные однородные дифференциальные уравнения высшего порядка с постоянными коэффициентами. Раздел 12. Кратные, криволинейные и поверхностные интегралы Тема 12.1. Двойной интеграл. Определение и основные свойства двойного интеграла. Методы нахождения двойных интегралов. Вычисление двойного интеграла в декартовой системе координат. Приложения двойного интеграла. Тема 12.2. Тройной интеграл. Определение и основные свойства тройного интеграла. Методы нахождения тройных интегралов. Вычисление тройного интеграла в декартовой системе координат. Приложения тройного интеграла. Тема 12.3. Криволинейные интегралы. Криволинейные интегралы 1-го и 2-го рода, их свойства и вычисление. Тема 12.4. Поверхностные интегралы. Поверхностные интегралы 1-го и 2-го рода, их свойства и вычисление. Раздел 13. Элементы теории поля Тема 13.1. Элементы теории поля. Скалярные и векторные поля. Векторные линии. Поток векторного поля через ориентированную поверхность и его вычисление. Поток вектора через замкнутую поверхность. Дивергенция векторного поля, ее свойства, вычисление и физический смысл. Циркуляция векторного поля, ее физический смысл. Ротор векторного поля, его свойства, вычисление и физический смысл. Раздел 14. Числовые и функциональные ряды Тема 14.1. Числовые ряды. Числовые ряды: определение, сумма ряда, сходимость. Необходимый признак сходимости. Знакоположительные ряды: признаки сравнения, Д’Аламбера и Коши, интегральный критерий. Знакопеременные ряды, абсолютная и условная сходимость. Знакочередующиеся ряды, признак Лейбница. Тема 14.2. Функциональные ряды. Функциональные ряды: понятие, сходимость, область сходимости. Абсолютная и условная сходимость ряда. Степенные ряды: определение, сходимость в точке и области. Радиус, интервал и область сходимости. Раздел 15. Ряд и интеграл Фурье Тема 15.1. Ряд Фурье. Тригонометрический ряд Фурье. Условие Дирихле. Разложение периодических функций в ряд Фурье. Разложение четных и нечетных функций в ряд Фурье. Тема 15.2. Преобразование Фурье. Интеграл Фурье. Косинус- и синус-преобразования Фурье и их свойства. Раздел 16. Теория функций комплексной переменной Тема 16.1. Функция комплексной переменной. Понятие функции комплексной переменной. Предел и непрерывность функции комплексной переменной. Тема 16.2. Производная и интеграл функции комплексной переменной. Производная функции комплексной переменной. Условия Коши – Римана. Аналитические функции. Интеграл от функции комплексной переменной, его вычисление и свойства. Интегральная теорема Коши, интегральная формула Коши. Тема 16.3. Ряды на комплексной плоскости. Числовые и функциональные ряды. Степенные ряды на комплексной плоскости. Ряд Тейлора. Ряд Лорана. Тема 16.4. Вычеты аналитических функций. Классификация нулей аналитических функций. Устранимые особые точки. Полюсы, их связь с нулями. Существенно особые точки. Вычеты аналитических функций, их вычисление. Основная теорема о вычетах. Вычеты в бесконечно удаленной точке. Полная сумма вычетов. Использование вычетов в вычислении интегралов. Задания контрольных работ Уважаемые студенты! Необходимо решить контрольные работы №3 и №4: вариант 1 решают те студенты, у которых последняя цифра номера зечетки нечетная; вариант 2 – у которых 0 или четная. Решенные и оформленые контрольные работы представляются преподавателю на первом практическом занятии летней сессии. На практическом занятии(в аудитории) необходимо будет решить аналогичные контрольные работы для допуска к экзамену. Возможно досрочное написание контрольных работ в дни консультаций заочников. Контрольная работа №3 Задание 1. Вычислите определенные интегралы. Вариант-1. а) 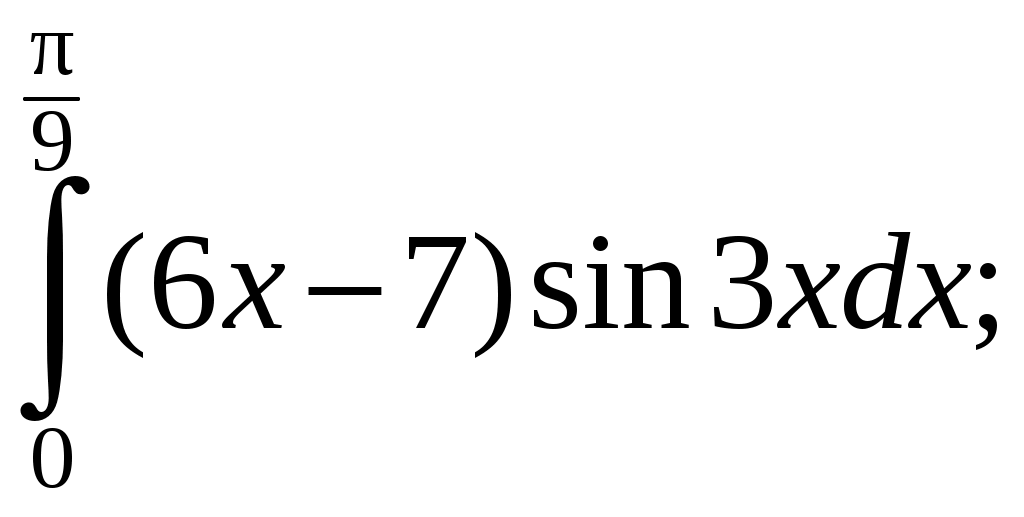 б) б) 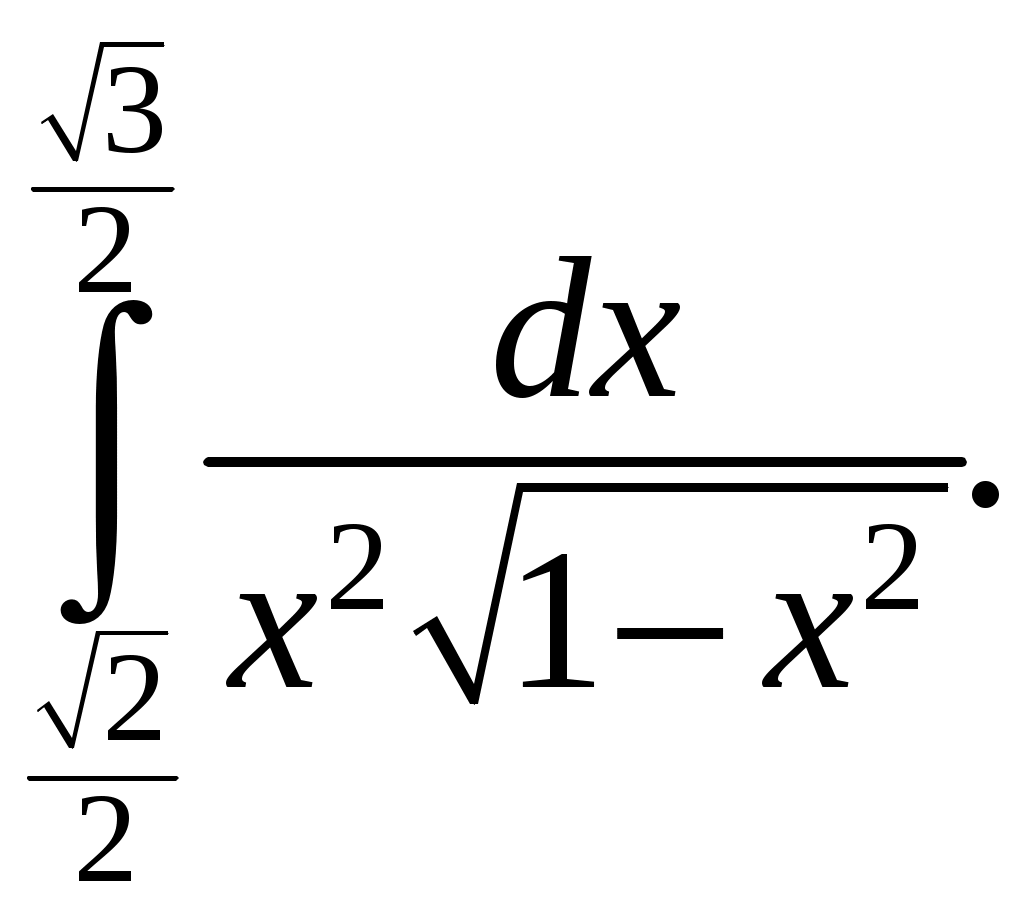 Вариант-2. а) 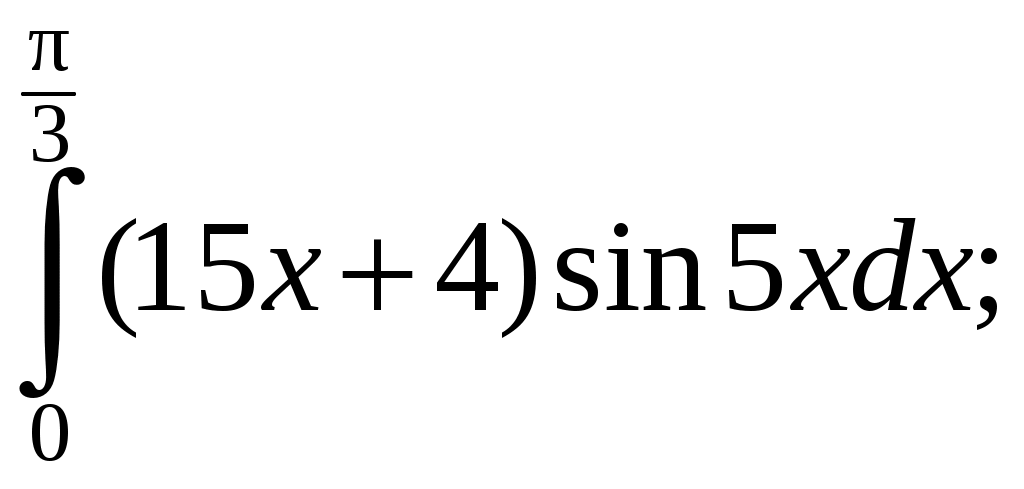 б) б) 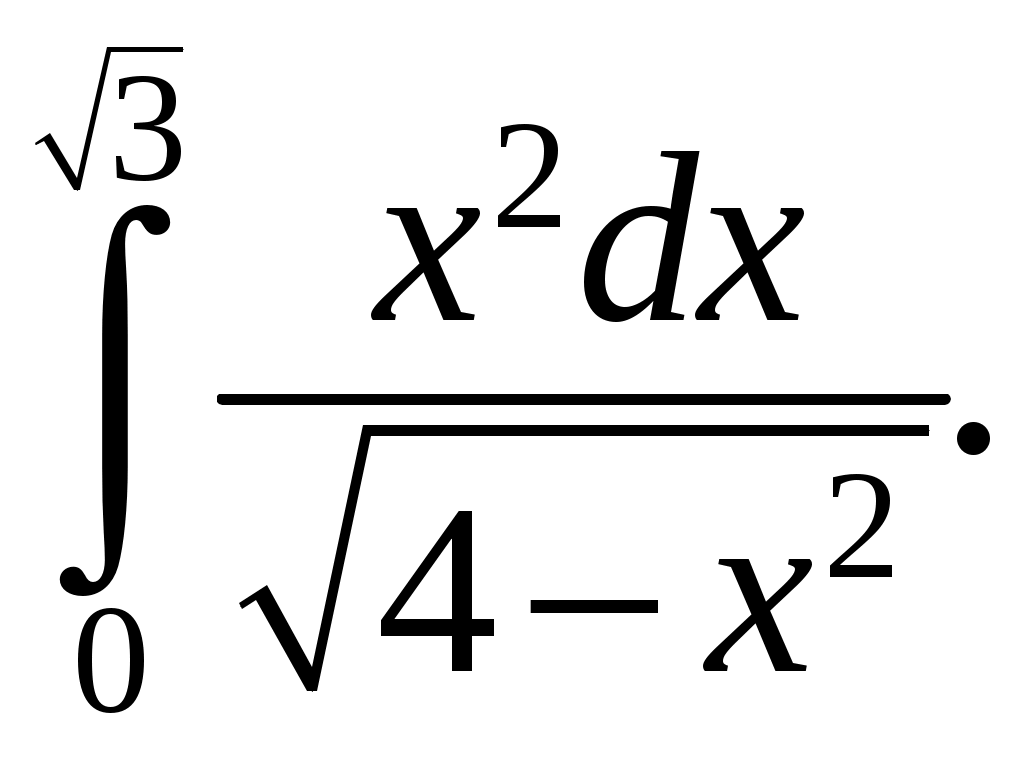 Задание 2. Вычислите площадь фигуры, ограниченной заданными линиями. Сделайте рисунок. Вариант-1. Вариант-2. Задание 3. Найдите общие решения дифференциальных уравнений. Вариант-1. а) Вариант-2. а) Задания 4. Решите задачу Коши при начальном условии Вариант-1. Вариант-2. Контрольная работа №4 Задание 1. Исследуйте сходимость числового ряда. Вариант-1. Варинт-2. 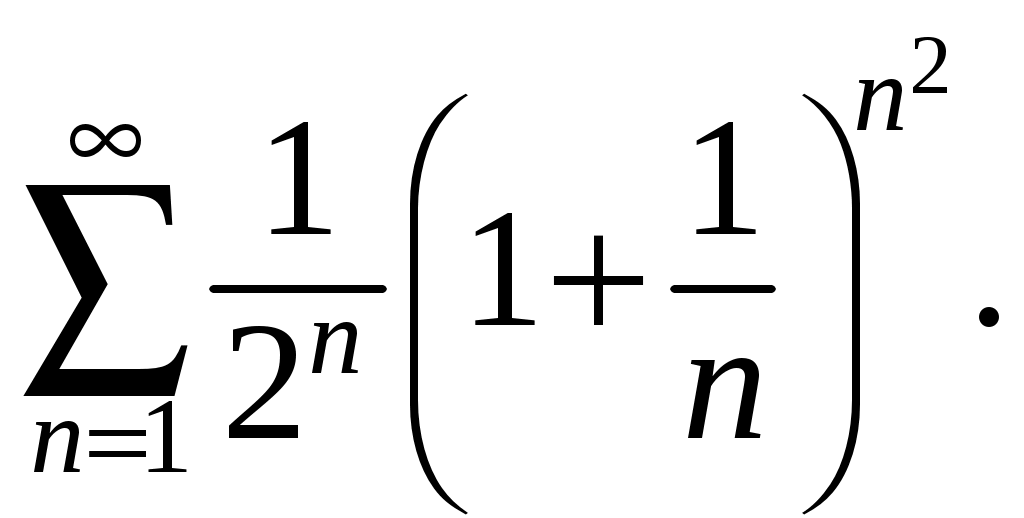 Задание 2. Найдите радиус и область сходимости степенного ряда, установите тип сходимости (абсолютная, условная сходимость). Вариант-1. Варинт-2. Задание 3. Вычислите определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд Маклорена. Вариант-1. 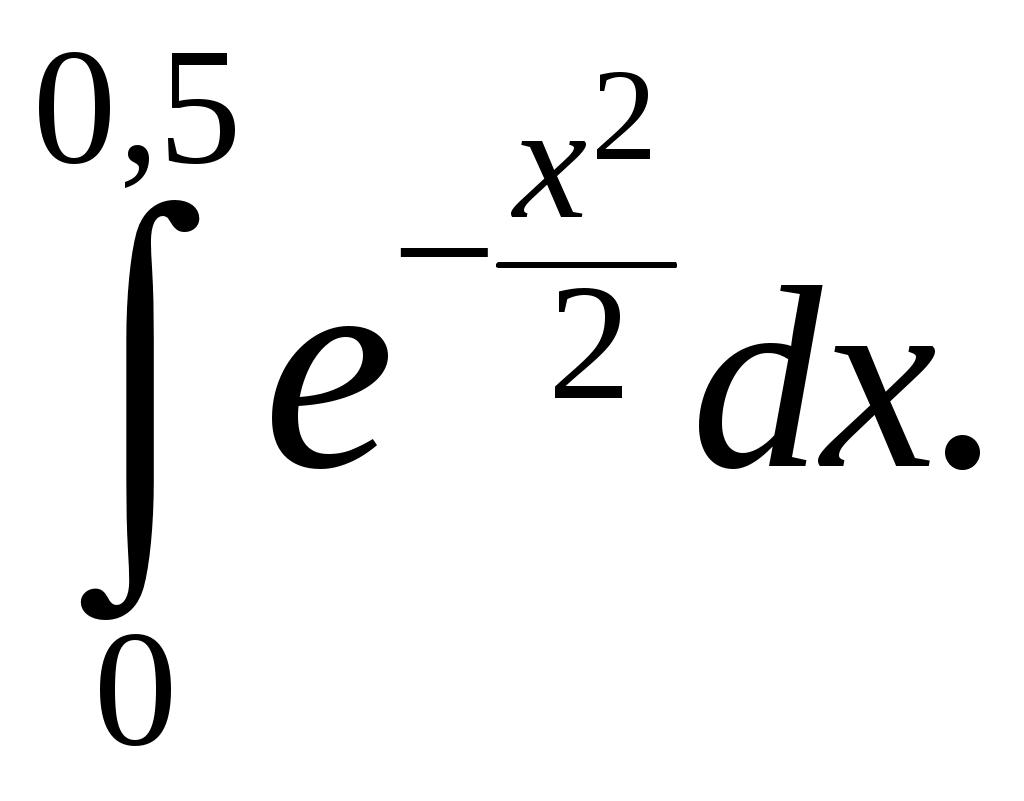 Вариант-2. 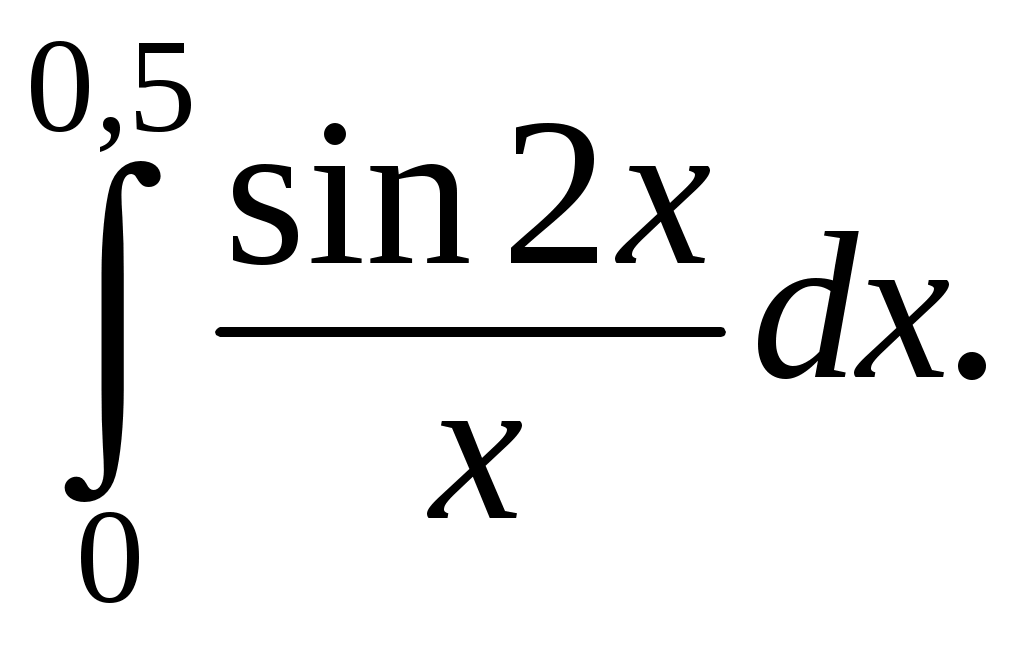 Задание 4. На промежутке 1) постройте график функции; 2) разложите функцию в ряд Фурье; 3) постройте график суммы ряда Фурье. Вариант-1. 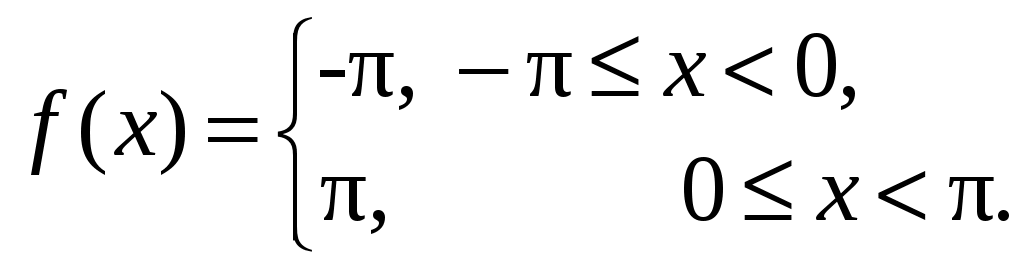 Вариант-2. 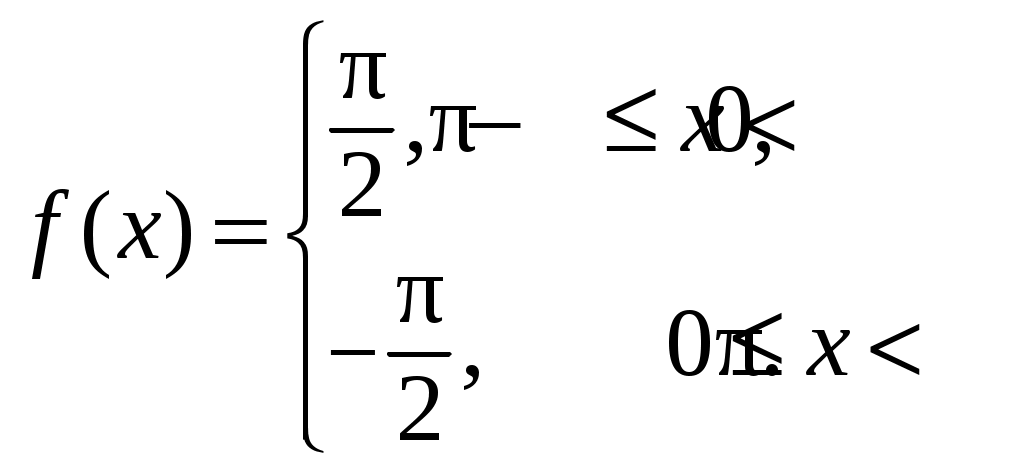 Задание 5. Вычислите заданный интеграл при помощи вычетов. Вариант-1. 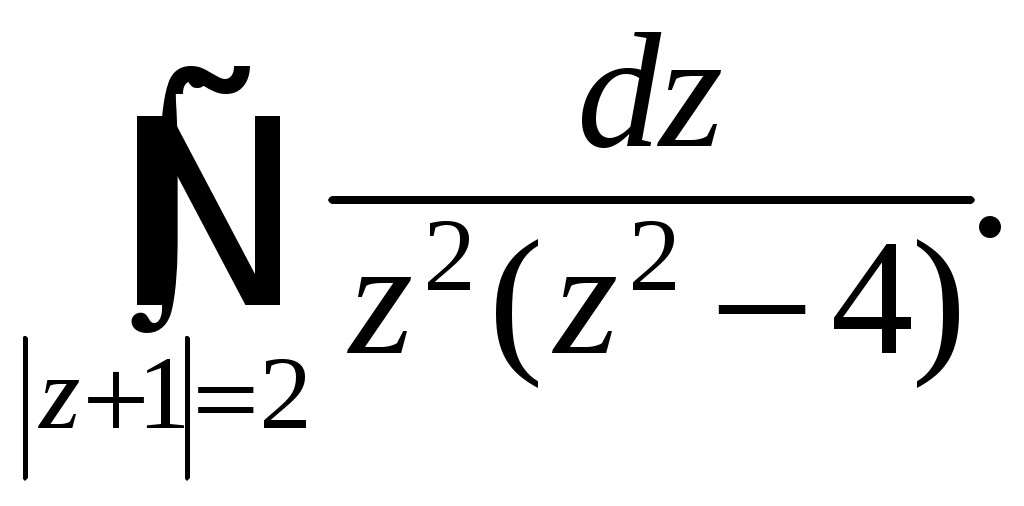 Вариант-2. 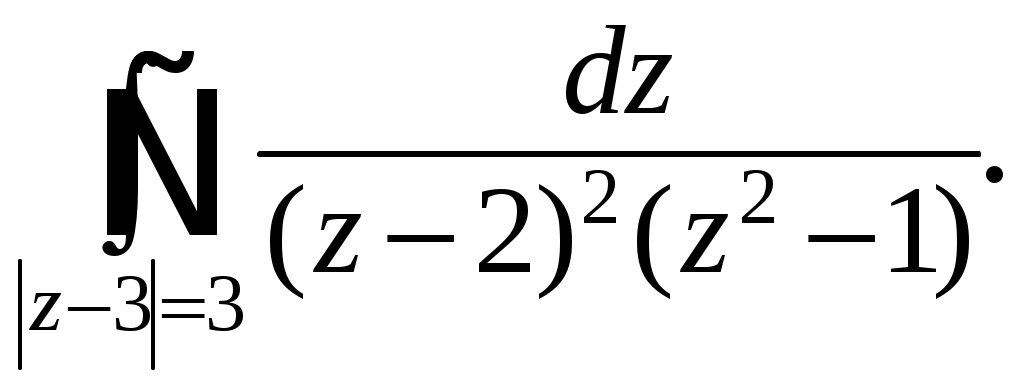 Рекомендуемая литература 1. Гусак, А.А. Высшая математика: учебник для студентов вузов: в 2 т. / А.А. Гусак. – Минск: ТетраСистемс, 1998. 2. Майсеня, Л.И. Справочник по высшей математике / Л.И. Майсеня, В.Э. Жавнерчик. – Минск: ТетраСистемс, 2010. – 272 с. 3. Письменный, Д.Т. Конспект лекций по высшей математике: полный курс / Д.Т. Письменный. – М.: Айрис-пресс, 2009. – 608 с. 4. Руководство к решению задач по высшей математике: учеб. издание: в 2 ч. / под общ. ред. Е.И. Гурского. – Минск: Вышэйшая школа, 1989. 5. Сухая, Т.А. Задачи по высшей математике: учеб. пособие: в 2 ч. / Т.А. Сухая, В.Ф. Бубнов. – Минск: Вышэйшая школа, 1993. Информация помещена на сайт ИИТ БГУИР 23.02.2015 г. Зав. кафедрой ФМД Л.И. Майсеня |
