task_283704 сопромт. Дифференциальные зависимости при кручении После интегрирования
 Скачать 435.45 Kb. Скачать 435.45 Kb.
|
|
Дифференциальные зависимости при кручении 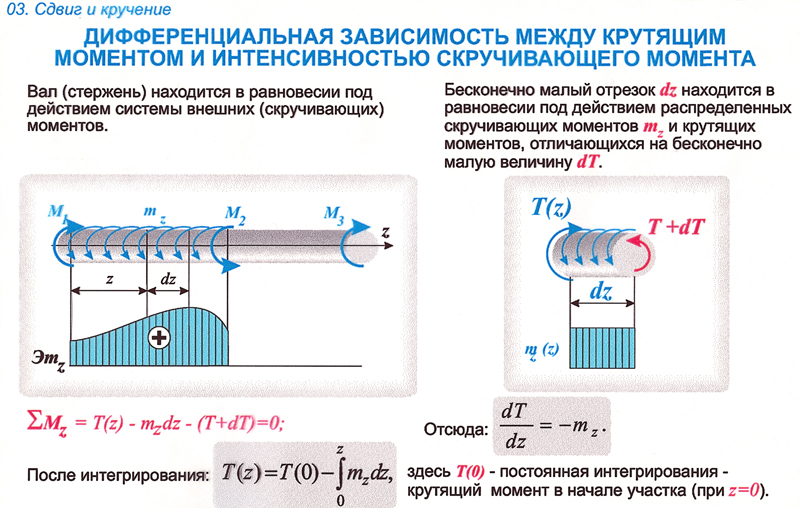 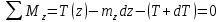 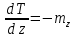 После интегрирования: 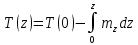 Определить значение и направление главных напряжений в опасной точке опасного сечения вала Определим напряжения, возникающие в произвольной точке рассматриваемого сечения (рис): 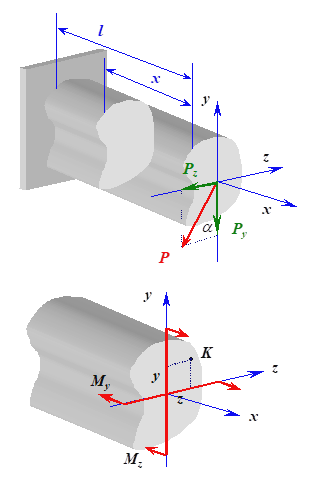 от изгибающего момента 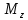 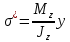 , ,от изгибающего момента 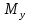 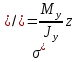 , ,здесь  и и 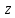 - координаты точки, в которой рассчитывают напряжения. - координаты точки, в которой рассчитывают напряжения.Знак напряжения зависит от характера деформации (растяжение-плюс, сжатие-минус). В нашем случае оба напряжения являются растягивающими и имеют знак плюс. На основании ПНДС полное нормальное напряжение в точке 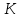 равно их алгебраической сумме: равно их алгебраической сумме: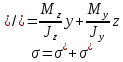 . .Объяснить способ Верещагина для определения интеграла Мора. Развернутая карта действий. Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр. 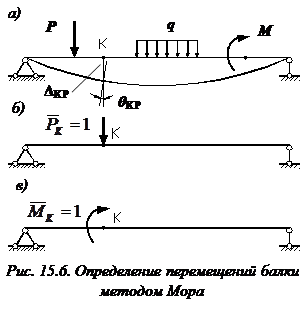 Рассмотрим балку, изображенную на рис. а. Обозначим 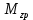 и и 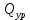 , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки ( , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки (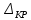 ) в точке K. ) в точке K.Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой 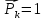 (рис.б). Единичную силу приложим в точке K, где нужно определить прогиб. (рис.б). Единичную силу приложим в точке K, где нужно определить прогиб.Внутренние усилия, возникающие во вспомогательной балке, обозначим 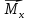 и и 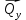 . .Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда 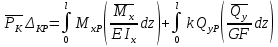 При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое). Тогда, учитывая, что 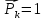 , окончательно получим формулу интеграла Мора: , окончательно получим формулу интеграла Мора: 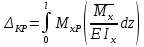 Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора. Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z. Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (θKP), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент 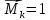 (рис.в). (рис.в).Какой из видов циклов нагружения - пульсационный или симметричный будет наиболее опасен при одинаковом максимальном напряжении? Ответ обосновать. 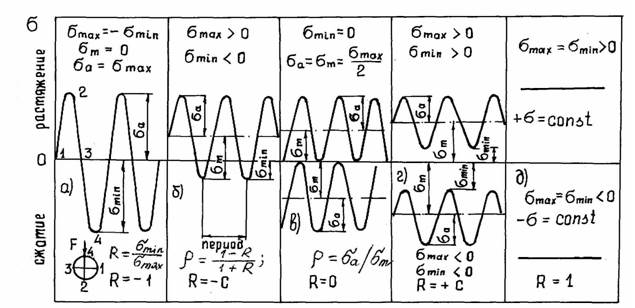  Если R=0 (σmin= 0; σm=σa=0,5σmax; ρ=1; а=0,5), то имеем отнулевой цикл напряжений (рис.1, в). Пульсирующеенагружение в соответствии с отнулевым циклом (когда напряжения изменяются от нуля до максимума) имеют: зубья зубчатых колес при работе в одну сторону, толкатели и шатуны тихоходных механизмов с малой нагрузкой холостого хода, нереверсивные валы (напряжения кручения). Если R=-1 (σm=0; σa=σmax; ρ=∞; а=1), то цикл напряжений называется симметричным (рис.1, а). Этот цикл является наиболее неблагоприятным для работы детали, так как характеризуются изменением не только значения, но и знака действующих напряжений (знакопеременный цикл). Здесь наибольшие и наименьшие напряжения противоположны по знаку и одинаковы по модулю (напряжения изгиба при вращении валов и осей). Есть два вала диаметрами 10 и 50 мм. Амплитудные напряжения в них одинаковы. Какой из валов будет наиболее прочный с точки зрения усталостной прочности и почему? Дать количественную оценку С точки зрения усталостной прочности вал с диаметром 50 мм будет прочнее, так как сечения его полярного момента будет больше, и как следствие коэффициенты усталостной прочности будут больше 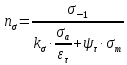 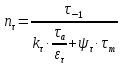 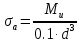 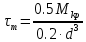 |
