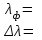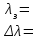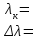Лаба по физике. Дифракция фраунгофера на решетке
 Скачать 445.71 Kb. Скачать 445.71 Kb.
|
|
0.Л а б о р а т о р н а я р а б о т а № 14-K ДИФРАКЦИЯ ФРАУНГОФЕРА НА РЕШЕТКЕ 1. ВВЕДЕНИЕ 1.1. С помощью дифракционной решетки можно произвести разложение немонохроматического (например, белого) света на спектральные составляющие. Дифракционная решетка широко применяется в различных спектрометрах, обеспечивая бóльшую разрешающую способность по сравнению с призменными спектрометрами. 1.2. Цель данной работы – определение длин волн линий излучения источника по измеренным углам дифракции и расчет дисперсии решетки. 2. ОСНОВНЫЕ ПОНЯТИЯ 2.1. Дифракция представляет собой совокупность явлений, наблюдаемых при распространении волн в резко неоднородной среде (например, вблизи границ тела, при прохождении волн сквозь отверстия), когда размеры неоднородностей L по величине сравнимы с длиной волны : L . В случае дифракции Френеля дифракционная картина создается сходящимися лучами. При дифракции Фраунгофера картина создается параллельными лучами, поэтому для наблюдения на их пути помещают собирающую линзу и устанавливают экран в её фокальной плоскости. 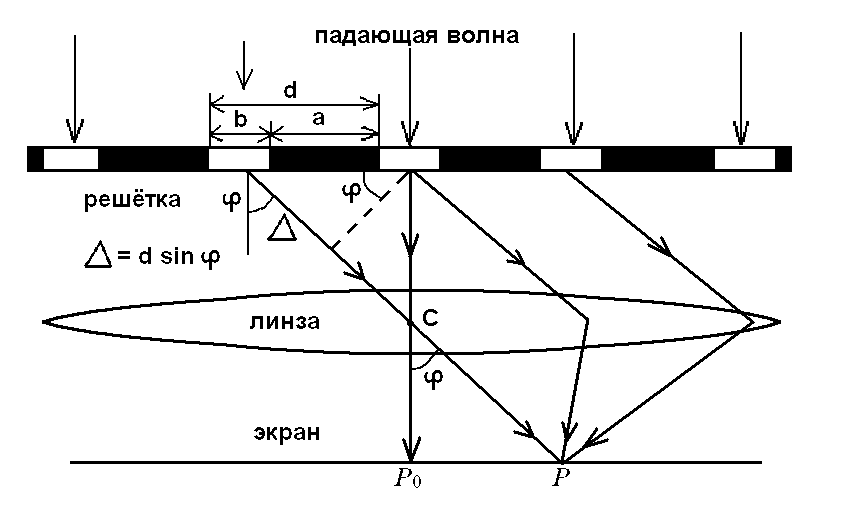 Рис. 1 2.2. Дифракционная решетка представляет собой строго периодическую структуру, состоящую из N одинаковых щелей шириной b в непрозрачном экране, отстоящих друг от друга на одно и то же расстояние a (рис.1). Величина d = а b называется периодом решетки. Наблюдаемая при дифракции Фраунгофера на решетке дифракционная картина представляет собой результат суммарной многолучевой интерференции волн от вторичных когерентных источников на каждой щели и на разных щелях. 2.3. Дифракция Фраунгофера на щели. Рассмотрим отдельную щель шириной b, на которую падает параллельный пучок лучей (рис. 2). 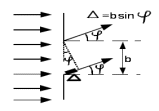 Рис. 2 Мы рассматриваем дифракцию лучей, отклоненных на один и тот же угол φ, и для их наблюдения поставим собирающую линзу, в фокальной плоскости которой расположим экран. Согласно принципу Гюйгенса-Френеля все точки фронта волны, совпадающего с плоскостью щели, можно рассматривать как точечные когерентные источники вторичных волн. а) При φ=0 эти волны приходят в точку наблюдения с одинаковой фазой и складываются в амплитуду А0 центрального максимума интенсивности (рис. 3). 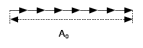 Рис. 3 б) Первый минимум интенсивности наблюдается при условии Δ = bsinφ = . Если разность хода лучей от краев щели составляет , а от краев одной зоны Френеля /2, значит на ширине щели укладываются две зоны Френеля, которые в данном случае имеют вид плоских полос, параллельных краю щели. Векторная диаграмма имеет вид, изображенный на рис. 4. 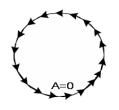 Рис. 4 Результирующая амплитуда равна нулю, так как волны от двух соседних зон Френеля полностью гасят друг друга. Условие k-го минимума имеет вид: bsin = k, где – длина волны, целые числа k (порядок минимума) принимают значения 1, 2, 3, 4,...При этом на ширине щели укладывается четное число зон Френеля, взаимно компенсирующих друг друга. в) Условие первого побочного максимума bsinφ = 3/2. Векторная диаграмма представлена на рис. 5. На ширине щели укладываются три зоны Френеля.  Рис. 5 Учитывая, что цепочка длиной А0 свернута в виде трех полуокружностей, где А0 = 3πR, а амплитуда А1 = 2R– диаметр окружности, найдем А1 = 2А0/(3π) и интенсивность J1 = 4J0/(9π2) ≈ 0,05 J0. Интенсивность первого побочного максимума не превышает 5% от интенсивности центрального максимума. Условие максимумов bsin ≈ (2k+ 1) /2 выполняется, когда на ширине щели укладывается нечётное число зон Френеля и волна от одной зоны оказывается нескомпенсированной. Т 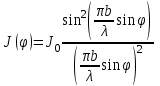 аким образом, каждая щель в отдельности дает дифракционную картину, представленную на рис. 6, где изображена зависимость интенсивности волны от синуса угла отклонения волны от первоначального направления (угла дифракции); (рассматривается случай нормального падения лучей на щель). 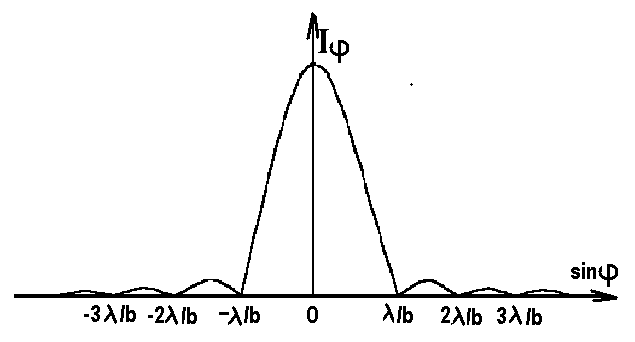  Рис. 6 2.4. Дифракция Фраунгофера на решетке Ввиду строго периодического расположения щелей в решетке когерентные волны, прошедшие через разные щели, будут интерферировать между собой и дадут четкую дифракционную картину. Как видно из рис. 1, разность хода волн, прошедших через соседние щели, равна: = dsin. (1) Следовательно, разность фаз этих волн 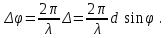 (2) (2)а) В центре картины (точка Р0 на рис. 1) наблюдается главный максимум нулевого порядка. При = 0 все волны приходят в точку наблюдения в одной фазе. Амплитуда волны А = N А0, где А0 – амплитуда волны, прошедшей через одну щель. Векторная диаграмма имеет вид, представленный на рис. 7. 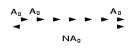 Рис. 7 Интенсивность волны J= N2 J0. Этот результат является следствием интерференции когерентных волн (N некогерентных источников дают интенсивность J= N J0). б) При углах , удовлетворяющих условию dsin= m , (3) разность фаз волн, прошедших через соседние щели, =m2/= =2m, и результат интерференции такой же, как в случае а (рис. 7), поскольку волны приходят в точку наблюдения в одной фазе. Условие (3) определяет главные максимумы m-го порядка, m=0,1,2,3... в) Между главными максимумами расположены минимумы и побочные максимумы. Условия минимумов:  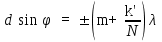 , (4) , (4)где k’ = 1, 2, 3, ..., N– 1. Эти минимумы интерференционные и обусловлены взаимным гашением волн, прошедших через все щели. Кроме них по-прежнему наблюдаются минимумы в направлениях, когда b sin = k, в которых каждая щель дает нулевую интенсивность. Интерференционные минимумы можно наглядно представить, пользуясь методом векторных диаграмм. На векторной диаграмме колебания, приходящие от первой, второй,…, N-й щели изобразятся векторами  одинаковой длины, углы между этими векторами равны разности фаз колебаний, что с учетом (4) будет составлять одинаковой длины, углы между этими векторами равны разности фаз колебаний, что с учетом (4) будет составлять 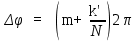 , ,при этом конец последнего вектора 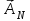 совпадет с началом первого совпадет с началом первого 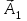 . К примеру, если рассматривать решетку с пятью щелями (N= 5) для m= 0 и k’ = 1, 2, 3, 4, где = (1/5)2, (2/5)2, (3/5)2, (4/5)2 соответственно, то мы получим векторные диаграммы вида (рис. 8): . К примеру, если рассматривать решетку с пятью щелями (N= 5) для m= 0 и k’ = 1, 2, 3, 4, где = (1/5)2, (2/5)2, (3/5)2, (4/5)2 соответственно, то мы получим векторные диаграммы вида (рис. 8): 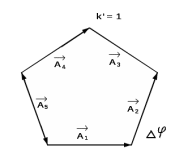 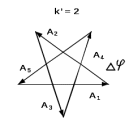  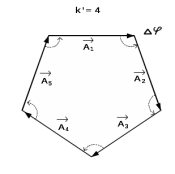 Рис. 8 Для других четверок значений k’ (m= 1, k’ = 1, 2, 3, 4; m= 2, k’ = 1, 2, 3, 4; и т. д.) векторы располагаются аналогично (при этом к просто добавляется 2, 4 и т.д.). Дифракционная картина выражена тем резче, чем больше число щелей N. Действительно, угловая ширина центрального максимума определяется условием первого минимума (4): Ndsin1 = или 21 = 2 arcsin 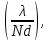 что в 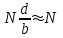 раз меньше, чем при дифракции на одной щели. Распределение интенсивности при дифракции Фраунгофера на решетке представлено на рис. 9. раз меньше, чем при дифракции на одной щели. Распределение интенсивности при дифракции Фраунгофера на решетке представлено на рис. 9.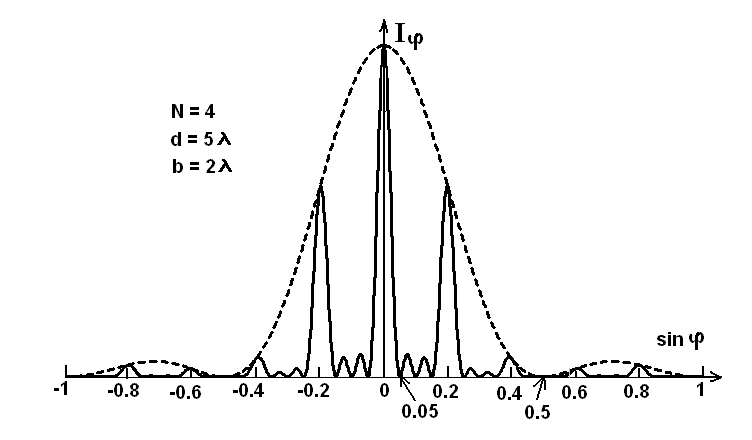 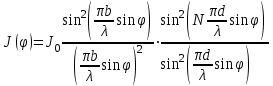  Рис. 9 Как видно из формулы (3), положение всех главных максимумов, кроме нулевого, зависит от длины волны. Поэтому главные максимумы различных длин волн будут разделены на экране; таким образом, дифракционная решетка будет производить разложение немонохроматического излучения на спектральные составляющие. Основные характеристики любого спектрального прибора – дисперсия и разрешающая сила. Дисперсия – угловое (или линейное) расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на 1 мкм). Угловая дисперсия D= /. Продифференцируем левую и правую части уравнения (3): dcos = m, откуда 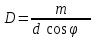 или при малых углах дифракции: или при малых углах дифракции: 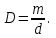 (5) (5)Линейная дисперсия D = DF, где F – фокусное расстояние линзы. Разрешающая сила определяется минимальной разностью длин волн δ, при которой две линии в спектре и + δ воспринимаются раздельно: R = /. Согласно критерию Рэлея, две линии в спектре воспринимаются раздельно (считаются разрешенными), если дифракционный максимум второй линии совпадает с минимумом первой линии (или лежит дальше него) (рис. 10). 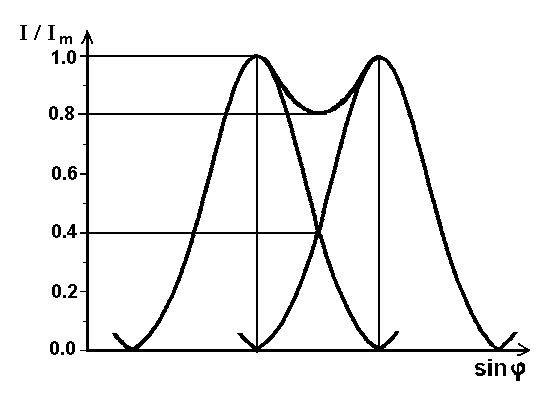  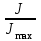 Рис. 10 При этом минимальная интенсивность составляет не более 80 % интенсивности максимумов и видны две отдельные линии. При более близком расположении видна одна слившаяся линия. Запишем условие m-го максимума для линии с длиной волны + δ и ближайшего минимума для линии с длиной волны : dsin = m( + ), dsin = (m + 1/N). Откуда m = /N и разрешающая сила дифракционной решетки R = / = mN. (6) Оригинальные дифракционные решетки создаются нанесением алмазным резцом на полированную стеклянную пластинку непрозрачных равноотстоящих штрихов (до тысячи штрихов на 1 мм длины). В учебной лаборатории применяют так называемые реплики, т.е. желатиновые отпечатки решетки, помещенные между двумя стеклянными плоскопараллельными пластинками. Используются также решетки, сделанные фотографическим способом. 3. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ 3.1. Измерение дифракционных углов производится с помощью гониометра. Внешний вид гониометра показан на рис. 11. Здесь 1 – микрометр, регулирующий ширину входной щели коллиматора 2 – фокусировочный винт коллиматора 3 – предметный столик 4 – фокусировочный винт зрительной трубы 5 – окуляр трубы 6 – окуляр, через который производятся отсчеты по шкале лимба, находящегося внутри прибора 7 – стопорный винт 8 – винт, производящий тонкое перемещение зрительной трубы. 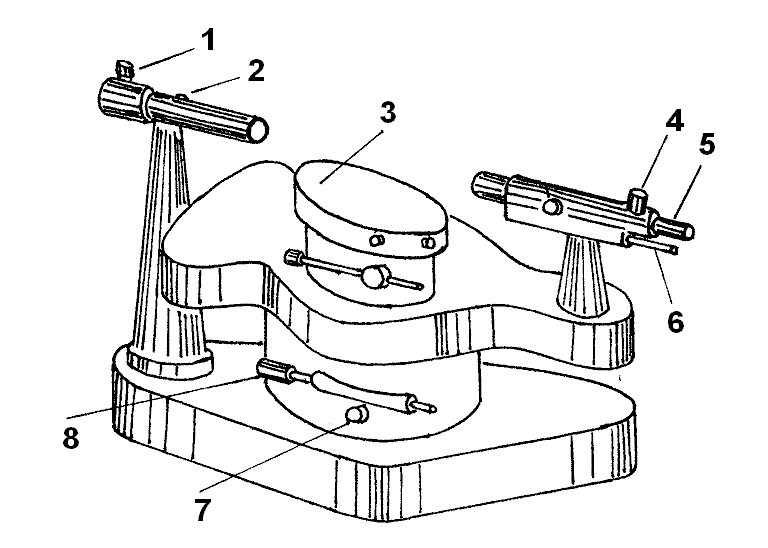 Рис. 11 Зрительная труба укреплена на подвижном кронштейне, который можно поворачивать вокруг вертикальной оси, проходящей через центр предметного столика. Поворот трубы осуществляется от руки после освобождения стопорного винта 7. При закрепленном винте можно производить тонкое перемещение трубы с помощью винта 8. Отсчет углов производится с помощью окуляра. При измерении используется верхняя шкала, по которой перемещается подвижная риска (рис. 12). Цена деления шкалы 20 угловых минут. 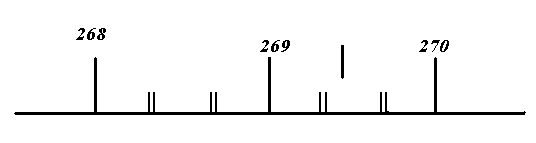 Рис.12 3.2. Техника безопасности При проведении лабораторной работы следует выполнять все требования техники безопасности. Помните, что гониометр и дифракционная решетка требуют осторожного обращения. 3.3. В качестве источника света в работе используется энергосберегающая лампа, дающая в видимой области несколько ярких спектральных линий, из которых измерения и расчеты проводятся на трех: фиолетовой, зеленой и красной. 4. ПОРЯДОК ИЗМЕРЕНИЙ 4.1. Технические данные лабораторной установки внести в табл. 1. Таблица 1
4.2. Измерение дифракционных углов 4.2.1. Включить лампу. 4.2.2. Произвести настройку гониометра так, чтобы щель и визирный крест были видны четко. 4.2.3. Установить дифракционную решетку на столик гониометра так, чтобы ее штрихи были вертикальны, а плоскость перпендикулярна оси коллиматора. 4.2.4. С помощью зрительной трубы просмотреть всю дифракционную картину и определить центральную полосу (рис. 13). 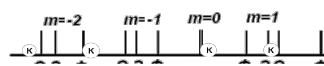 Рис .13 При =0 условие (3) выполняется для всех длин волн, поэтому центральная полоса не окрашена. Выбрать цвет линии и установить зрительную трубу на линию первого порядка, слева от центральной полосы. Снять отсчет с помощью окуляра 6, и полученное значение –1 внести в табл. 2. Зрительную трубу навести на линию первого порядка, справа от центральной полосы, и измерить +1, также записав в табл. 2. Угол дифракции определить по формуле 1 = +1 – –1/2. (7) Аналогичные измерения провести для спектров второго порядка данной линии. Измерения проводятся для всех трех длин волн, наблюдаемых в спектре источника. Таблица 2
5. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 5.1. Определение длины волны 5.1.1. Вычислить длину волны каждой линии по формуле (3): = (dsin) / m, где m – порядок спектра. Вычисление провести по измеренным значениям углов дифракции 1 и 2. Результаты записать в табл. 3. Таблица 3
5.1.2. Оценить систематическую абсолютную погрешность определения длины волны по формуле = (d cos) / m, где – приборная погрешность гониометра, выраженная в радианах (1 = /(60180) рад). Результаты записать в табл. 3. 5.2. Определение угловой дисперсии решетки Для двух близко расположенных линий – зеленой и красной –рассчитать угловую дисперсию по экспериментальным значениям углов дифракции, взяв их из табл. 2, и – из табл. 3: 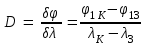 – в случае первого порядка и – в случае первого порядка и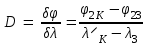 – в случае второго порядка. – в случае второго порядка. В расчетах выражать в радианах, – в мкм. Сравнить полученные результаты с теоретическими значениями D, рассчитанными по формуле (5). Результаты записать в табл. 4. Таблица 4
КОМПЛЕКТЫ ВОПРОСОВ ДЛЯ ЗАЩИТЫ РАБОТЫ I КОМПЛЕКТ 1. В чем заключается явление дифракции? При каких условиях это явление наблюдается? 2. Рассчитайте разрешающую силу используемой дифракционной решетки для спектра первого порядка, считая, что длина решетки 5 см. 3. Постройте векторную диаграмму для расчета амплитуды волны при дифракции Фраунгофера на щели, при условии b sin = . II КОМПЛЕКТ 1. Что такое дифракционная решетка? Напишите условие наблюдения главных максимумов при дифракции Фраунгофера на решетке. 2. Рассчитайте разрешающую силу используемой дифракционной решетки для спектра второго порядка, считая, что длина решетки 5 см. 3. Постройте векторную диаграмму для расчета амплитуды волны при дифракции Фраунгофера на щели, при условии b sin = 3/2. III КОМПЛЕКТ 1. Как изменится дифракционная картина (рис. 3) при d = 2b? 2. Чему равен максимальный порядок спектра, который можно получить с помощью данной дифракционной решетки? 3. Постройте векторную диаграмму для расчета амплитуды волны при дифракции Фраунгофера на решетке при условиях, определяемых формулой (4), где считать N = 12, k’ = 2. IV КОМПЛЕКТ 1. Объясните расположение линий в наблюдаемом дифракционном спектре. 2. Дайте определение разрешающей силы дифракционной решетки. Как она связана с числом щелей дифракционной решетки? 3. Постройте векторную диаграмму для расчета амплитуды волны при дифракции Фраунгофера на решетке при условиях, определяемых формулой (4), где считать N = 6 , k’ = 1. V КОМПЛЕКТ 1. Дайте определение угловой и линейной дисперсий дифракционной решетки. Как они связаны с периодом решетки? 2. Каково различие между дифракционным и призматическим спектрами одного и того же источника света? 3. Постройте векторную диаграмму для расчета амплитуды волны при дифракции Фраунгофера на щели, при условии bsin = 2. VI КОМПЛЕКТ 1. Что называют дифракцией Фраунгофера на щели? Как изменится характер дифракционной картины при увеличении ширины щели? 2. Как связана интенсивность главных максимумов при дифракции Фраунгофера на решетке с числом щелей в решетке? 3. Постройте векторную диаграмму для расчета амплитуды волны при дифракции Фраунгофера на решетке при условии dsin= 5. Авторы описания профессор М.Я. Юшина и доцент Е.А. Гусева. | |||||||||||||||||||||||||||||||||||||||||||||