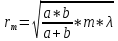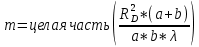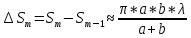Лекция Дифракция. Дифракция света

• Название: Дифракция света
• Дата: 08.04.2022
• Размер: 143.87 Kb.
• Имя файла: Лекция Дифракция.docx
• Тип: Лекция; #455434

Лекция
ДИФРАКЦИЯ СВЕТА. зоны Френеля
Любые отклонения в распространении света от законов геометрической оптики называются дифракцией света. К законам геометрической оптики относятся:

1. 
   в однородной среде свет распространяется прямолинейно;
   
2. 
   законы отражения;
   
3. 
   законы преломления.
   

Для объяснения явления дифракции используют принцип Гюйгенса-Френеля:

а) принцип Гюйгенса – всякая точка среды, до которой дошло колебание (волна) является источником вторичной волны;

б) принцип Френеля – направление распространения луча света определяется интерференцией вторичных волн.

Лучи света, исходящие из точки S, создают на сферической волновой поверхности в точках S₁, S₂, S₃ колебания, являющиеся источниками когерентных вторичных волн (см. рис. 1). В результате интерференции вторичных волн лучи света отклоняются от своего первоначального направления н а угол α. Отклонения происходит на неоднородностях среды или на диафрагмах, соответствующих размеров.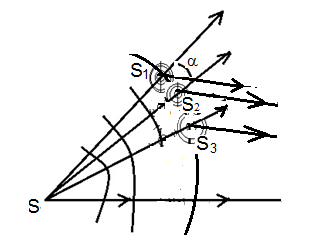


Рисунок 1.
Зоны Френеля.

Применим принцип Гюйгенса-Френеля для нахождения амплитуды светового колебания, возбуждаемого в точке P сферической волной, распространяющейся в однородной среде из точечного источника S (см. рис. 2). Волновая поверхность такой волны симметрична относительно прямой SP. Поэтому разобьём волновую поверхность ФОФ на кольцевые зоны таким образом, что расстояние от краёв каждой зоны до точки P отличаются на 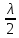(λ – длина световой волны в той среде, в которой распространяется волна). Как видно из рисунка 2: SO=а – радиус волновой поверхности; OP=b – расстояние от вершины волновой поверхности (т. О) до точки P. Тогда расстояние b_m от внешнего края m-й зоны до точки P равно:

(1)

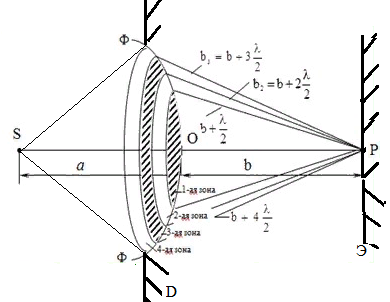Рисунок 2.
Используя рисунок 2 и геометрические преобразования, можно определить радиус r_m внешней границы m-й зоны:

(2)

Например, если расстояние от источника до диафрагмы SD ≈ а=1м; расстояние от диафрагмы до экрана DЭ ≈ b=1м, длина световой волны в данной среде λ=500нм, то радиус центральной зоны (m=1) равен: r₁=0,5мм.

Очевидно, радиус последней зоны и, следовательно, число открытых зон определяется радиусом диафрагмы R_D:

(3)

Например, если расстояние от источника до диафрагмы SD ≈ а=1м; расстояние от диафрагмы до экрана DЭ ≈ b=1м, длина световой волны в данной среде λ=500нм, радиус диафрагмы R_D =0,5см, то число открытых зон Френеля равно: m=100.

Площадь поверхности ΔS_m каждой кольцевой зоны, примерно, одинаков:

(4)

Следовательно, каждая зона излучает, примерно, одинаковое количество энергии в единицу времени. Но вклад каждой зоны в результирую освещенность точки Р разный, так как он определяется 1) углом α между нормалью к поверхности зоны и направлением от неё в точку Р (см. рис. 1); 2) оптической разностью хода Δ световых волн приходящих в точку Р: от двух соседних зон Δ= 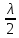, поэтому колебание от одной зоны приходит в противофазе к колебанию соседней зоны и в точке Р будет наблюдаться

• 
  интерференционный максимум, если диафрагмой D открыто нечётное число зон: m=2n+1 – max;
  
• 
  интерференционный минимум, если открыто чётное число зон: m=2n – min.
  

где m– число открытых зон Френеля.

Так как вклад в результирующую амплитуду А_р колебаний в точке Р каждой последующей зоны монотонно убывает (угол α возрастает с ростом m), то амплитуда m-й зоны равна полусумме ограничивающих её зон:



Тогда результирующая амплитуда А_р световых колебаний в точке Р:

при открытах двух зонах (т=2) равно: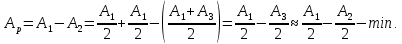



при открытах трёх зонах (т=3) равно: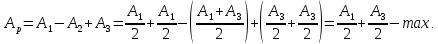



Если открыта только центральная зона (m=1), то A_p=A₁; если открыты все зоны (диафрагма отсуствует), то , так как А_∞ → 0.
φ

Лекция
Дифракция Фраунгофера. ДИФРАКЦИОННАЯ РЕШЕТКА.
Пусть на диафрагму ДД, представляющая собой узкую щель (длина щели много больше её ширины), падает плоская световая волна длиной λ, волновая поверхность которой, параллельна плоскости щели (см. рис. 3). (Волновая поверхность – это огибающая множества точек среды, имеющих одинаковую фазу колебания).

Поместим за щелью ДД двояковыпуклую линзу ЛЛ, а в фокальной плоскости линзы – экран ЭЭ.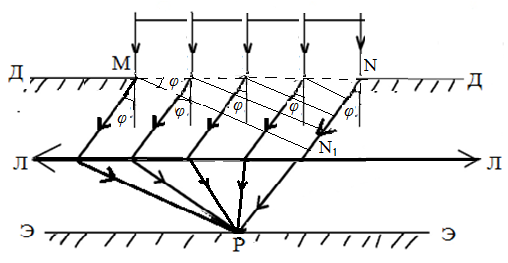


Рисунок 3.
Все точки открытого фронта волны MN являются источниками вторичных волн, направление которых варьируется от угла дифракции φ=0 до φ = ±π/2. Параллельные лучи, имеющие один и тот же угол отклонения φ соберутся линзой ЛЛ в некоторой точке Р экрана ЭЭ. Фронт волн MN развернётся в положение MN₁. Оптические пути MР и N₁Р одинаковы и разность фаз между колебаниями исходящими из точки M и колебаниями исходящими из точки N образуется из-за оптической разности хода NN₁=∆. Как видно из рисунка ∆=а·sinφ., где а – ширина щели. Разделив ∆ на отрезки, равные λ/2, найдем число зон Френеля в щели: m=Δ/(λ/2). Как было сказано в лекции 11, фазы колебаний, возбужденных соседними зонами, противоположны, поэтому вторичные волны от соседних зон полностью гасят друг друга. Поэтому в точке Р будет наблюдаться интерференционный минимум, если число открытых зон щели чётное – m=2n:

минимум, если а·sinα=(2п)∙(λ/2), где п – целое. число;

(1)

в точке Р будет наблюдаться интерференционный максимум, если число открытых зон щели чётное – m=2n+1:

максимум, если а·sinφ=(2п+1)∙(λ/2); где п – целое. число.

(2)

При φ=0 мы имеем центральный интерференционный максимум в точке фокуса линзы ЛЛ. В этом случае щель ДД действует как одна зона Френеля, так как от точек М и N оптическая разность хода ∆=0.
ДИФРАКЦИОННАЯ РЕШЕТКА
Дифракционной решеткой называется совокупность большого числа N одинаковых, отстоящих друг от друга на одно и то же расстояние b щелей шириной a (см. рис. 4).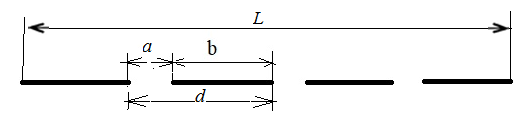


Рисунок 4.
Параметры дифракционной решётки: а – ширина щели; b – расстояние между щелями; d=a+b –постоянная, или период решетки; L – длина решётки; N=L/d – число щелей решётки. Дифракционная решётка, в которой все щели расположены в одной плоскости, называется одномерной дифракционной решеткой.

Пусть на одномерную дифракционную решетку ДД падает плоская световая волна длиной λ, волновая поверхность которой, параллельна плоскости решётки (см. рис. 4).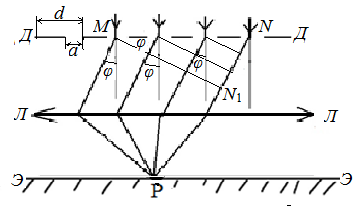



Рисунок 5.

Все точки открытого фронта волны MN являются источниками вторичных волн, направление которых варьируется от угла дифракции φ=0 до φ = ±π/2. Параллельные лучи, имеющие один и тот же угол отклонения φ соберутся линзой ЛЛ в некоторой точке Р экрана ЭЭ. Фронт волн MN развернётся в положение MN₁. Оптические пути MР и N₁Р одинаковы и разность фаз между колебаниями исходящими из точки M и колебаниями исходящими из точки N образуется из-за оптической разности хода NN₁=∆. В каждой щели можно выделить одинаковое число зон Френеля. Поэтому, если в каждой щели открыто чётное число зон (m=2n), то, согласно формуле (1), каждая щель создаст в точке Р интерференционный минимум и мы получаем условие главного минимума:

главный минимум, если а·sinα=(2п)∙(λ/2), где п – целое. число;

(1)

Если в каждой щели открыто нечётное число зон (m=2n+1), то, согласно формуле (2), каждая щель создаст в точке Р интерференционный максимум. При этом возможно:

а) интерференционные максимумы имеют в точке Р одинаковую фазу колебаний и взаимно усиливаются, то есть мы получаем главный максимум. Это возможно, если на оптической разности хода NN₁=∆ укладывается целое число волн ∆=n*λ – условие главного максимума:

главный максимум, если d·sinα=п∙λ, где п – целое. число;

(3)

б) интерференционные максимумы в точке Р от соседних щелей колеблются в противофазе ( 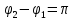) и поэтому световые колебания взаимно гасятся полностью, если число щелей чётное, или почти полностью, если число щелей нечётное, то есть мы получаем в точке Р добавочный минимум. Это возможно, если на оптической разности хода NN₁=∆ укладывается нечётное число полуволн ∆=(2n+1)*(λ/ 2):

добавочный минимум, если d·sinφ=(2п+1)∙(λ/2), где п – целое число.

(4)

Примечание.

1. 
   В формулах (1) - (4) число п называется «порядок максимума / минимума».
   
2. 
   Количество наблюдаемых главных максимумов можно определить из формулы (3), зная, что |sin φ| ≤ 1: .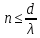
   

Семинар «Дифракция»

1. 
   Вычислить радиус m-й зоны Френеля, если расстояние от источника до зонной пластинки равно a; расстояние от пластинки до места наблюдения равно b; длина световой волны . По полученной в общем виде формуле найти радиус первой зоны, если a=b=10 м, =4500 Å.
   
2. 
   Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого r можно менять. Расстояние от диафрагмы до источника и экрана равны a=100 см и b=125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r₁=1,00 мм и следующий максимум при r₂=1,29 мм.
   
3. 
   Монохроматический свет падает нормально на щель ширины b=11 мкм. За щелью находится тонкая линза с фокусным расстоянием f=150 мм, в фокальной плоскости которой расположен экран. Найти длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка (на экране) равно x=50 мм.
   
4. 
   Плоская монохроматическая волна нормально падает дифракционную решетку с периодом d=1,0 мм. Под углом φ=3,0 на экране образуется фраунгоферов максимум второго порядка. Найти длину волны света. Определить количество наблюдаемых максимумов для данной длины волны.