|
|
оптика, дифракция. свет это дело темное. Волновая поверхность
Волновой фронт – ГМТ, до которых доходят колебания к моменту времени t. Представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Есть только один, все время перемещается.
Волновая поверхность – ГМТ, колеблющихся в одинаковой фазе. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. То есть волновых поверхностей существует бесконечное множество. Остаются неподвижными. Могут быть любой формы. В простейших случаях имеют форму плоскости или сферы, то есть волна плоская или сферическая. В изотропной и однородной среде волна, порождаемая точечным источником, сферическая.
Дифракция света
Принципиальное отличие дифракции от интерференции, состоит в том, что дифракция – это огибание препятствий или отверстий, встречающихся на их пути, а интерференция – это усиление или ослабление света на экране.
Дифракция – отклонение распространения пучка света от законов геометрической оптики, т.е. огибание светом контура непрозрачных тел. Дифракция проявляется при прохождении светом через среду с ярко выраженными неоднородностями. Например, при прохождении через дифракционную решетку.
Интерференция– сложение в пространстве двух (или более) волн в пространстве, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны.
Для экспериментов по дифракции используется препятствия для света (дифракционная решетка и т.д.) и один пучок света или одна волна.
Т.е., кроме экрана обязательно используется какое-либо препятствие, либо щели в непрозрачном материале, либо дифракционная решетка и т.д. В опытах по интерференции в одном месте должны встретиться две когерентные волны или два пучка света, при этом использование каких-либо приспособлений, кроме экрана не обязательно.
Принцип Гюйгенса
В приближении геометрической оптики свет за преградой не должен проникать в область геометрической тени. Однако в действительности световая волна в принципе распространяется во всем пространстве за преградой, проникая в область геометрической тени, причем это проникновение тем более существенно, чем меньше размеры отверстий. При диаметре отверстий или ширины щелей, сравнимых с длиной волны света, приближение геометрической оптики оказывается совершенно неправомерно.
Способ, позволяющий найти положение фронта волны в любой момент времени t+∆t по его известному положению в момент времени t.
Принцип Гюйгенса гласит: каждая точка, до которой доходит световое возмущение, сама становится источником вторичных полусферических волн, огибающая которых представляет собой фронт распространяющейся волны.
П усть, например, плоская волна встречает на своем пути экран со щелью (рис. 2.1). Как только волна доходит до щели, каждая точка открытой части волнового фронта становится источником вторичных полусферических волн. Огибающая этих волн дает новое положение фронта волны. усть, например, плоская волна встречает на своем пути экран со щелью (рис. 2.1). Как только волна доходит до щели, каждая точка открытой части волнового фронта становится источником вторичных полусферических волн. Огибающая этих волн дает новое положение фронта волны.
Этот принцип не позволял произвести количественный расчет дифракционной картины, т.е. найти интенсивность волн, распространяющихся в различных направлениях. Кроме того, принцип Гюйгенса не позволял ответить на вопрос, как согласовать явление дифракции с наблюдаемым на опыте прямолинейным распространением света.
При этом осталось непонятным, почему при распространении волны не возникает обратная волна.
Принцип Гюйгенса – Френеля
Френель дополнил принцип Гюйгенса идеей интерференции вторичных полусферических волн. Пусть, например, сферическая поверхность S представляет собой положение волнового фронта в некоторый момент времени (рис. 2.2). Вторичные волны, идущие от этого фронта волны, налагаются друг на друга и интерферируют.
К огибающей все вторичные волны приходят в одинаковых фазах, и их интерференция приводит к большой интенсивности света. Вторичные волны, идущие от волнового фронта вперед, вступают в свободное от возмущений пространство. Они интерферируют только друг с другом. Напротив, вторичные волны, идущие назад, вступают в пространство, где уже есть волновое возмущение – прямая волна. При интерференции вторичные волны гасят прямую волну, так что после прохождения волны пространство за ней оказывается невозмущенным.
Принцип Гюйгенса-Френеля гласит: окружим все источники света S1, S2, S3, … произвольной замкнутой поверхностью F (см. рисунок в тетради). Каждую точку такой поверхности можно рассматривать как источник вторичных волн, распространяющихся во всех направлениях. Эти волны когерентны, так как все они возбуждаются одними и теми же первичными источниками. Световое поле, возникающее в результате их интерференции, в пространстве вне поверхности F совпадает с полем реальным источников света.
Волна, отделившаяся от своих источников, в дальнейшем ведет автономное существование, совершенно не зависящее от наличия источников.
Ч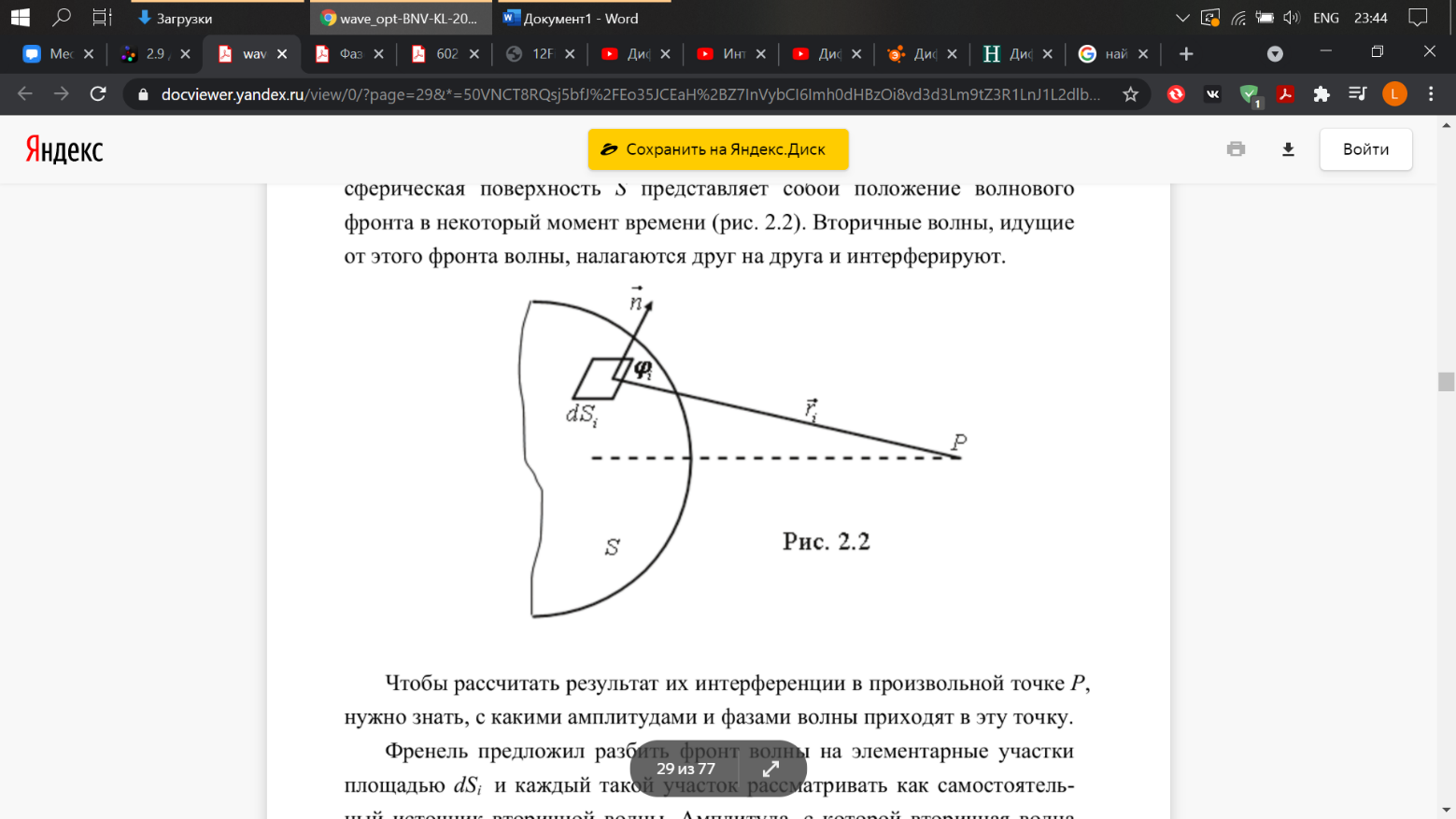 тобы рассчитать результат интерференции вторичных волн в произвольной точке Р, нужно знать, с какими амплитудами и фазами волны приходят в эту точку. тобы рассчитать результат интерференции вторичных волн в произвольной точке Р, нужно знать, с какими амплитудами и фазами волны приходят в эту точку.
Френель предложил разбить фронт волны на элементарные участки площадью dSi и каждый такой участок рассматривать как самостоятельный источник вторичной волны. Амплитуда, с которой вторичная волна приходит в точку наблюдения Р, прямо пропорциональна площади участка dSi, обратно пропорциональна расстоянию от участка до рассматриваемой точки ri, а также зависит от угла φi между нормалью n к данному участку dSi и направлением ri на рассматриваемую точку. С увеличением φi амплитуда волны убывает, стремясь к нулю при стремлении φi к π/2. Фаза волны зависит от расстояния ri, которое проходит волна до точки наблюдения Р.
Если Ео – амплитуда колебаний вектора Е в электромагнитной волне, то колебание, дошедшее в виде волны до точки наблюдения на экране, запишется в виде
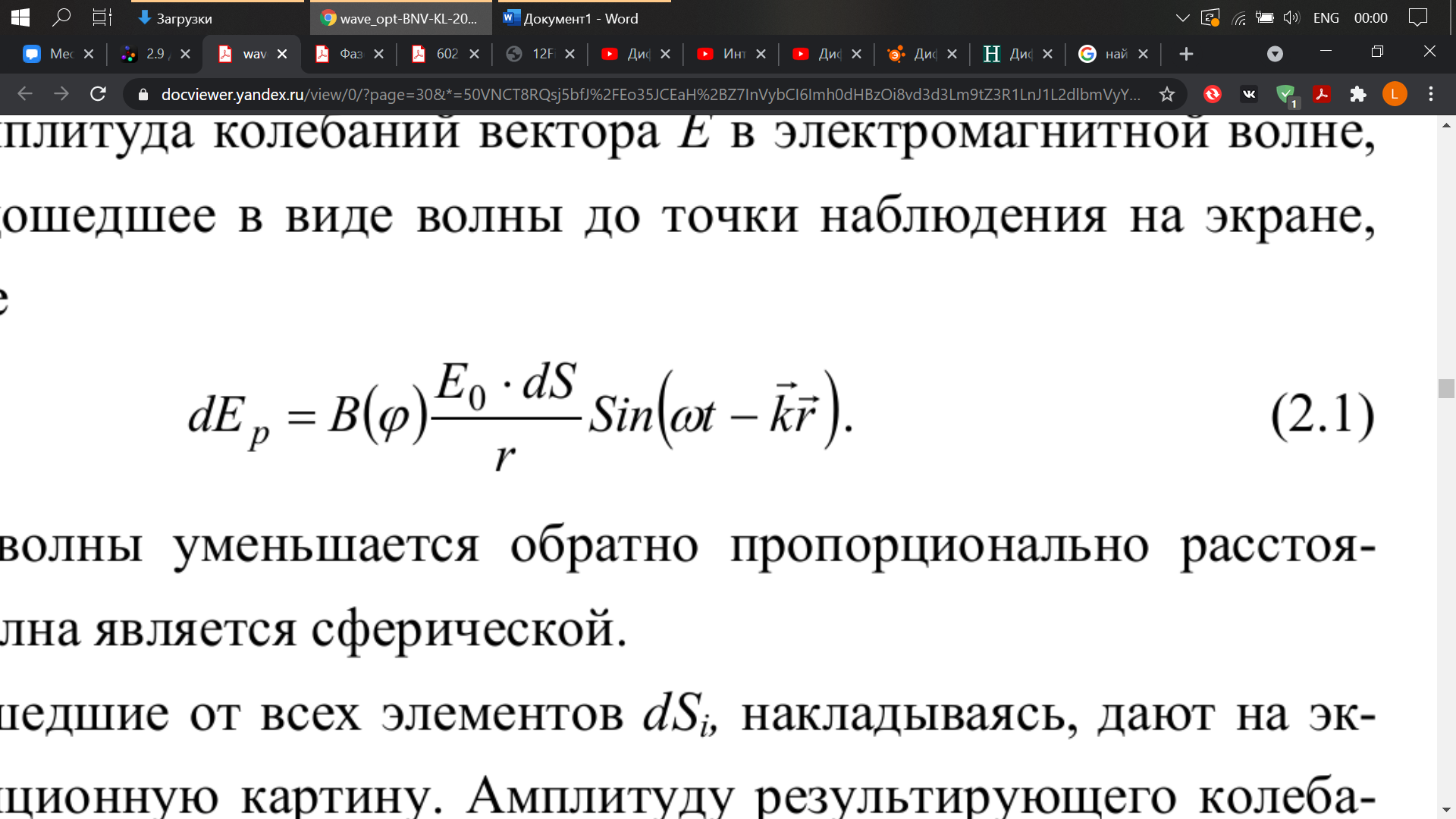
Амплитуда волны уменьшается обратно пропорционально расстоянию r, так как волна является сферической.
Волны, пришедшие от всех элементов dSі, накладываясь, дают на экране интерференционную картину. Амплитуду результирующего колебания, возбуждаемого в точке Р вторичными световыми волнами, можно получить интегрированием выражения (2.1) по всем элементам поверхности S:
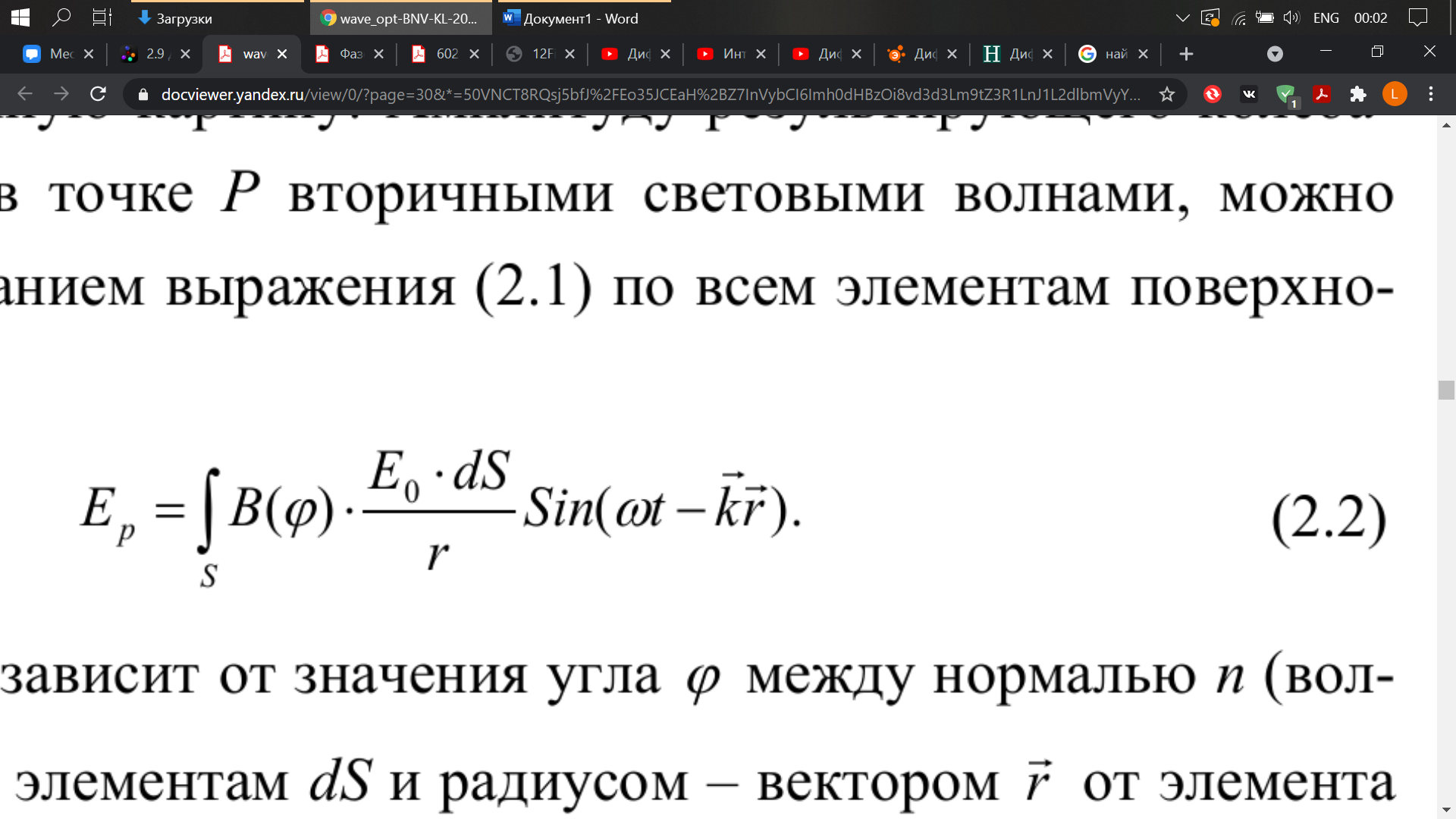
Множитель B(ϕ) зависит от значения угла ϕ между нормалью n (волновым вектором k) к элементам dS и радиусом – вектором r от элемента dS до точки наблюдения Р. Величина В имеет максимальное значение, равное единице, для угла ϕ = 0 и минимальное значение, равное нулю, для ϕ =π/2. В общем случае, когда фронт волны имеет произвольную форму, определение амплитуды результирующей волны представляет собой чрезвычайно трудную задачу. Но в некоторых частных случаях этот принцип позволил объяснить ряд дифракционных явлений, а также устранить одно из основных затруднений волновой теории света, показав, как согласуется явление дифракции с законом прямолинейного распространения света.
Метод зон Френеля. Прямолинейность распространения света
Френель решил задачу о прямолинейном распространении света, применив чрезвычайно наглядный приём, получивший название метода зон Френеля. Рассмотрим этот метод.
П усть в однородной среде от точечного источника S распространяется световая сферическая волна. В центре экрана (рис. 2.3) в точке Р определим амплитуду результирующего колебания, возбуждаемого этой волной. Фронт волны симметричен относительно прямой, соединяющей источник света S с точкой наблюдения Р. Он разбивается на кольцевые зоны следующим образом. усть в однородной среде от точечного источника S распространяется световая сферическая волна. В центре экрана (рис. 2.3) в точке Р определим амплитуду результирующего колебания, возбуждаемого этой волной. Фронт волны симметричен относительно прямой, соединяющей источник света S с точкой наблюдения Р. Он разбивается на кольцевые зоны следующим образом.
К расстоянию ОР = b добавляется отрезок, равный половине длины волны (λ/2), и из точки Р радиусом b1 = b + λ/2 на фронте волны проводится окружность. Получается первая зона. Затем к расстоянию b1 добавляется еще λ/2 и радиусом b2 = b + 2λ/2 из точки Р на фронте волны проводится следующая окружность. Получается еще одна зона и т.д. Зона с номером m проводится радиусом bm = b+m λ/2. Благодаря такому построению зон расстояния от краев двух соседних зон до точки наблюдения Р отличаются на λ/2.
Каждая зона рассматривается как самостоятельный источник вторичной волны. Разность хода волн, приходящих в точку Р от двух соседних зон, равна λ/2. Это значит, что волны будут иметь в точке Р противоположные фазы. Поэтому амплитуда результирующего колебания, вызванного совместным действием двух соседних зон в точке Р, будет равна разности амплитуд колебаний, возбуждаемых каждой зоной в отдельности.
Тогда амплитуда результирующего колебания, возбуждаемого всеми зонами волнового фронта, будет определяться выражением
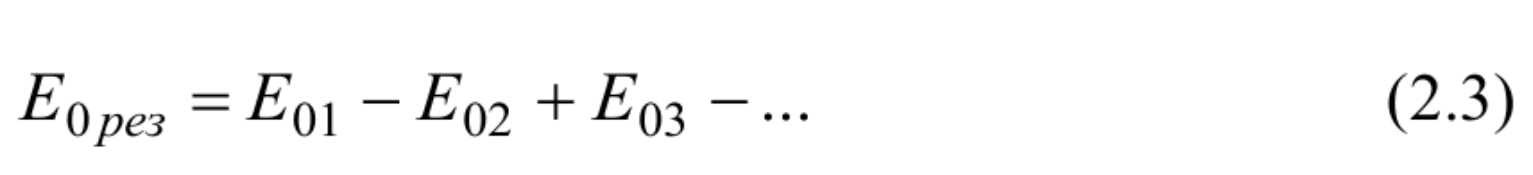 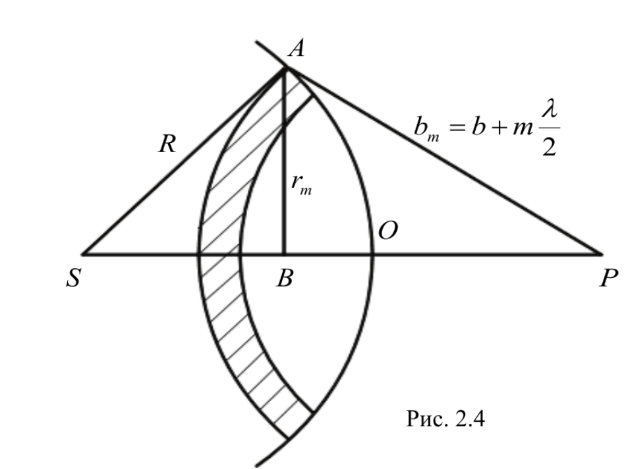
Амплитуда колебания, возбуждаемого в точке Р волной, приходящей от отдельной m-зоны, согласно принципу Гюйгенса – Френеля зависит от площади 0 зоны ∆Sm, от расстояния bm и угла φm между нормалью, восстановленной к соответствующей зоне, и направлением bm на точку наблюдения.
Определим площадь m-ной зоны. Обозначим радиус m-ной зоны AB как rm, высоту сферического сегмента ОВ как hm (рис. 2.4).
Из треугольников SAB и ABP

к оль- оль-
Из формулы (2.9) следует, что площади кольцевых зон с точностью до членов, содержащих λ2, не зависят от номера зоны, т.е. одинаковы. Расстояние bm от края зоны до точки наблюдения и угол ϕm увеличиваются с увеличением номера зоны. Это означает, что с увеличением номера зоны амплитуда колебания, возбуждаемого в точке Р этой зоной, убывает
E01 > E02 > ...
Если длина волны λ мала по сравнению с b и bm, а это всегда имеет место для световых волн, то с достаточным приближением ряд чисел E01, E02,… можно рассматривать как арифметическую прогрессию. И тогда для амплитуд Е0,т−1, Е0,т и Е0,т+1 будет справедливо соотношение
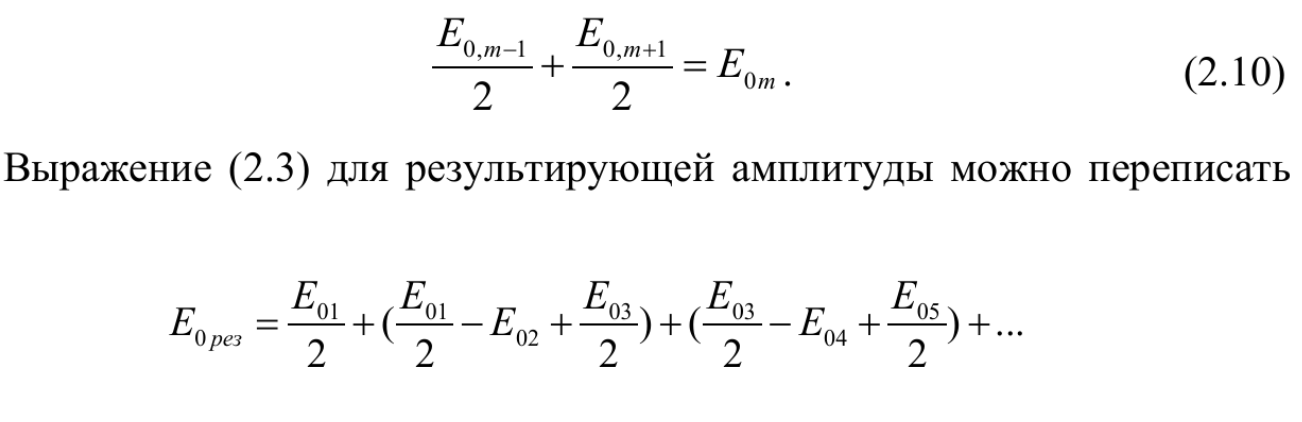
С огласно условию (2.10) выражения в скобках будут равны нулю. Тогда огласно условию (2.10) выражения в скобках будут равны нулю. Тогда
Это означает, что амплитуда результирующего колебания, возбуждаемого в точке Р полностью открытым сферическим фронтом, равна половине амплитуды колебания, возбуждаемого одной лишь центральной зоной.
Пользуясь формулой (2.6), оценим размеры этой зоны для зеленого света. Если принять b = R = 1 м, а λ = 500 нм, то r1 0,5 мм.
Следовательно, свет от точечного источника S распространяется как бы в пределах узкого прямого канала, т.е. практически прямолинейно.
Решим задачу о распространении света от источника до точки Р методом графического сложения амплитуд. Разобьем волновую поверхность на кольцевые зоны, аналогичные зонам Френеля, но гораздо меньше по ширине (разность хода от краев зоны до точки Р составляет одинаковую для всех зон малую долю длины волны). Колебание, создаваемое в точке Р каждой из зон, изобразим в виде вектора, длина которого равна амплитуде колебания, а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания. Амплитуда колебаний, создаваемых такими зонами в точке Р, медленно убывает при переходе от зоны к зоне. Каждое следующее колебание отстает от предыдущего по фазе на одну и ту же величину. Следовательно, векторная диаграмма, получающаяся при сложении колебаний, возбуждаемых отдельными зонами, имеет следующий вид (см. рисунок в тетради).
Дифракция от круглого отверстия и круглого экрана
Метод зон Френеля позволил решить ряд задач по дифракции света.
В качестве примера рассмотрим случай дифракции от круглого отверстия.
С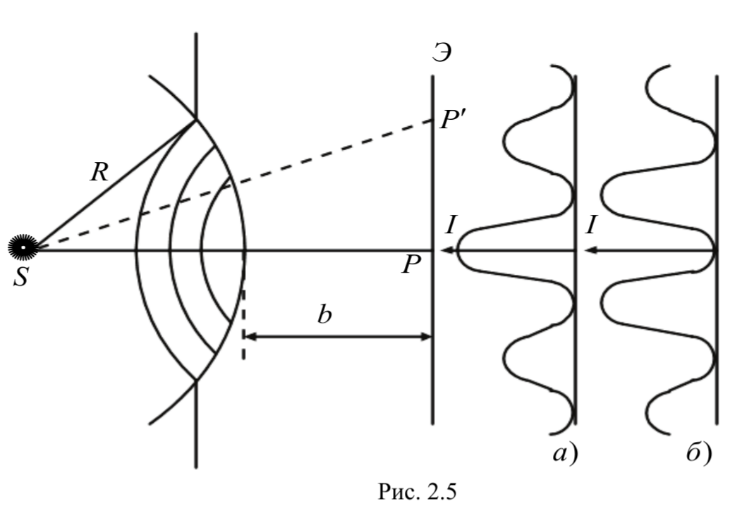 ферическая световая волна встречает на своем пути непрозрачный экран с круглым отверстием радиуса r0. Экран расположен так, что перпендикуляр, опущенный из источника света S на плоскость экрана, попадает в центр отверстия (рис. 2.5). Дифракционная картина наблюдается на экране Э, расположенном параллельно плоскости отверстия. В рассматриваемом случае открытым будет не весь фронт волны, а только та его часть, которая совпадает с отверстием. Построим на этой части волнового фронта зоны Френеля. Предположим, что число этих зон равно т. Тогда амплитуда результирующего колебания, возбуждаемого в точке Р вторичными световыми волнами, определится выражением ферическая световая волна встречает на своем пути непрозрачный экран с круглым отверстием радиуса r0. Экран расположен так, что перпендикуляр, опущенный из источника света S на плоскость экрана, попадает в центр отверстия (рис. 2.5). Дифракционная картина наблюдается на экране Э, расположенном параллельно плоскости отверстия. В рассматриваемом случае открытым будет не весь фронт волны, а только та его часть, которая совпадает с отверстием. Построим на этой части волнового фронта зоны Френеля. Предположим, что число этих зон равно т. Тогда амплитуда результирующего колебания, возбуждаемого в точке Р вторичными световыми волнами, определится выражением
E0 рез = E01 − E02 + ...± E0m, (2.12)
где знак “+” соответствует нечетному значению m, a “–“ – четному.
Преобразуем выражение (2.12):
E0 рез = E01/2 + (E01/2 − E02 + E03/2) ...± E0m/2, (2.13)
Из рассуждений, приведенных в предыдущей теме, следует, что выражения в скобках равны нулю.
Поэтому
E0 рез = E01/2 + E0m/2, когда m – нечетное (2.14)
и
E0 рез = E01/2 – E0m/2, когда m – четное. (2.15)
Число зон на открытой части волнового фронта можно определить, исходя из того, что радиус m-ной зоны совпадает с радиусом отверстия
rm = r0 (2.16)
Подставим выражение (2.6) в (2.16) и возведем обе части равенства в квадрат

П реобразуем это соотношение к виду реобразуем это соотношение к виду
Таким образом, число зон на открытой части волнового фронта зависит от соотношения между радиусом отверстия r0 и длиной волны λ, а также от расстояний b и R.
Если r20 того же порядка, что и λ, число зон m будет мало. Число зон может быть мало и при значительных размерах отверстия, если только R и b достаточно велики.
При малых значениях m амплитуды колебаний, возбуждаемых в точке Р первой и m-ой зонами мало отличаются друг от друга
E0 ≈ E0m.
Тогда, согласно формулам (2.14) и (2.15) при нечетном числе зон m
E0p = E01,
а при четном m
E0p = 0.
Это означает, что в случае, когда размеры отверстия малы (m – мало), на экране будет наблюдаться дифракционная картина, в центре которой будет светлое или темное пятно в зависимости от числа зон, укладывающихся в отверстии. При четном числе зон в центре будет темное пятно, при нечетном – светлое. В других точках экрана будет наблюдаться та или иная освещенность в зависимости от их расстояния до центра экрана.
Рассмотрим, например, точку P′ (рис. 2.5). Для нее прямая SP′ не является осью симметрии открытой части фронта волны. Ограниченная краями отверстия картина зон Френеля для точки P′ имеет вид, показанный на рисунке 2.6. Нечетные зоны заштрихованы. Зоны частично закрыты непрозрачным экраном. Поэтому действие этих зон в точке P′ определяется не только их числом, но и тем, какая часть к аждой из зон открыта. Точный подсчет амплитуды результирующего колебания в точке P′ сложен, но ясно, что при удалении от центра дифракционной картины периодически встречаются места с большей или меньшей освещенностью. аждой из зон открыта. Точный подсчет амплитуды результирующего колебания в точке P′ сложен, но ясно, что при удалении от центра дифракционной картины периодически встречаются места с большей или меньшей освещенностью.
Если действие открытых частей нечетных зон перевесит действие открытых частей четных зон (или наоборот), то в точке P′ будет наблюдаться максимум интенсивности, только более слабый, чем в центре картины. Если действие открытых частей четных и нечетных зон взаимно компенсируется, то наблюдается минимум интенсивности.
Из соображений симметрии очевидно, что вся картина будет иметь вид чередующихся темных и светлых колец с центром в точке P. Чем дальше точка P′ находится от точки P, тем слабее интенсивность максимума.
Зависимость интенсивности I света от расстояния r от центра дифракционной картины изображена на рисунке 2.5а (m – нечетное) и 2.5б (m –четное). При больших размерах отверстия r20 >> λ число зон Френеля, укладывающихся на открытой части фронта волны, велико, поэтому E01 >> E0m.
Из равенства (2.13) следует, что в этом случае
E0рез =E01/2
То есть, результат получается такой же, как и для полностью открытого волнового фронта – свет распространяется прямолинейно. Пользуясь методом зон Френеля, нужно всегда иметь в виду, что он является лишь приближенным расчетным приемом, заменяющим строгое решение задачи. Отыскание точных решений связано со столь большими математическими трудностями, что пока они найдены лишь для некоторых простейших случаев дифракции.
Из теории Френеля можно получить еще ряд замечательных, иногда парадоксальных следствий. Одно из них – возможность использования в роли собирающей линзы зонной пластинки.
Если на пути монохроматической световой волны поместить пластинку, на которой в месте расположения всех четных зон нанесены концентрические кольца из непрозрачного материала, то в точку наблюдения будут приходить колебания только от нечетных зон, происходящие в одной и той же фазе:
Е0 рез = Е01 + Е03 + Е05 + ......+ Е0(2k +1).
В результате интерференции этих колебаний должен возникнуть максимум: освещенность в точке Р должна значительно возрасти, после того как почти половина площади отверстия будет закрыта непрозрачным экраном! Опыт полностью подтверждает правильность этого предположения. Действие зонной пластинки не опровергает, как это может показаться, закона сохранения энергии. Закрывание половины зон непрозрачным экраном сопровождается не только увеличением амплитуды световых колебаний в точке наблюдения, но и одновременно уменьшением амплитуды световых колебаний в других точках, т. е. зонная пластинка действует подобно собирающей линзе. Полная энергия светового потока, проходящего через зонную пластинку, равна лишь половине энергии светового потока, который проходит через отверстие в отсутствие этой пластинки.
Второе замечательное следствие теории Френеля – предсказание существования светлого пятна в области геометрической тени от непрозрачного круглого экрана. Если на пути распространения света от точечного источника поместить небольшой непрозрачный экран, закрывающий одну или несколько зон, то чтобы найти освещенность в центре области геометрической тени, нужно рассчитать результат сложения волн от всех оставшихся незакрытыми зон. В центре геометрической тени всегда должно быть светлое пятно, освещенность которого равна освещенности, создаваемой половиной первой незакрытой зоны Френеля, отсчитываемой от края экрана. Для наблюдения светлого пятна в области геометрической тени необходимо, чтобы непрозрачный экран перекрывал небольшое число зон Френеля (одну – две), а размеры неровностей на краю его поверхности не превышали длины световой волны. Распределение интенсивности света на экране будет аналогично, показанному на рисунке 2.5а.
Фазовая зонная пластинка
Для расчета дифракционных картин Френель предложил приближенный способ, основанный на представлении о зонах Френеля. Из определения зон Френеля для точки наблюдения Р следует, что световые волны, испускаемые четными зонами Френеля, приходят в точку Р в одной фазе, а нечетными – в противоположенной. Таким образом, волны от четных и нечетных зон взаимно ослабляют друг друга. Если каким-либо способом «выключить» все четные или все нечетные зоны, можно получить существенное увеличение суммарной напряженности электрического поля и, соответственно, интенсивности света в точке Р. Эта идея лежит в основе простого оптического устройства, называемого зонной пластинкой Френеля.
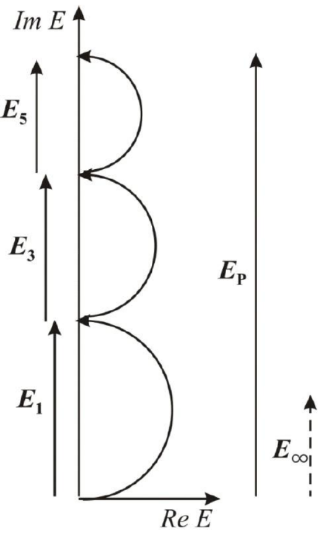 На рис.1 показана векторная диаграмма сложения амплитуд напряженностей полей в точке Р, созданных нечетными зонами Френеля. На рис.1 показана векторная диаграмма сложения амплитуд напряженностей полей в точке Р, созданных нечетными зонами Френеля.
Р ис.1.Векторная диаграмма для зонной пластинки Френеля. Векторы Е1, Е3, Е5, … изображают вклады в амплитуду суммарного поля открытых нечетных зон Френеля. Амплитуда суммарного поля ЕР многократно превышает амплитуду поля Е∞, которое наблюдалось бы в точке Р в отсутствии зонной пластинки. ис.1.Векторная диаграмма для зонной пластинки Френеля. Векторы Е1, Е3, Е5, … изображают вклады в амплитуду суммарного поля открытых нечетных зон Френеля. Амплитуда суммарного поля ЕР многократно превышает амплитуду поля Е∞, которое наблюдалось бы в точке Р в отсутствии зонной пластинки.
В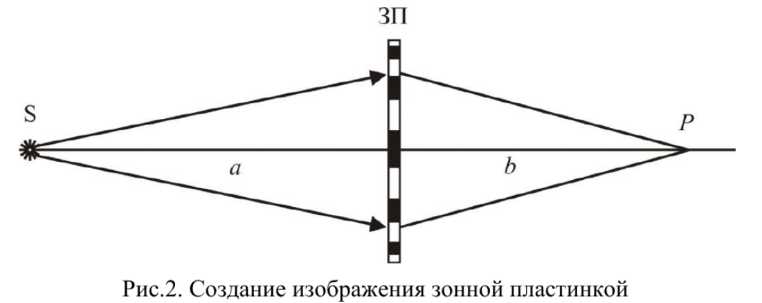 идно, что зонная пластинка существенно увеличивает амплитуду (и интенсивность) светового поля в точке Р. Поскольку зонная пластинка не может увеличить мощность падающей на нее световой волны, то следует сделать вывод, что она перераспределяет энергию в пространстве, сосредотачивая её в определенных областях. Другими словами, зонная пластинка фокусирует свет, аналогично тому, как это делает линза. идно, что зонная пластинка существенно увеличивает амплитуду (и интенсивность) светового поля в точке Р. Поскольку зонная пластинка не может увеличить мощность падающей на нее световой волны, то следует сделать вывод, что она перераспределяет энергию в пространстве, сосредотачивая её в определенных областях. Другими словами, зонная пластинка фокусирует свет, аналогично тому, как это делает линза.
Расстояние от точечного источника до зонной пластинки а (рис.2) и от зонной пластинки до точки наблюдения Р связаны с радиусами зон Френеля rm следующим соотношением (1):
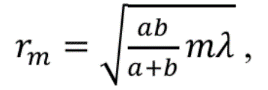
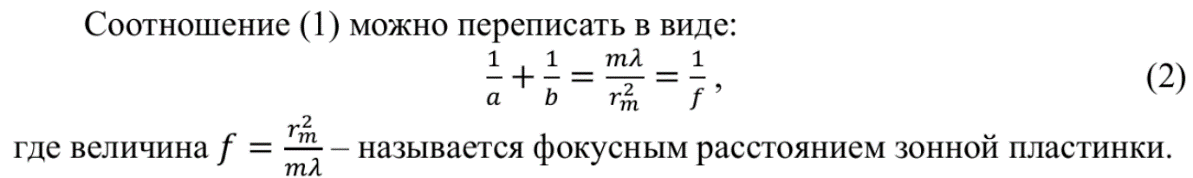
Характерной особенностью зонной пластинки по сравнению с линзой являет то, что ее фокусное расстояние зависит от длины волны. Это явление называют хроматизмом. Чем больше длина волны, тем меньше фокусное расстояние.
Фокусирующее действие зонной пластинки будет наблюдаться и в случае, когда в каждой открытой кольцевой зоне будет укладываться по 3, 5,… и т.д. зон Френеля. Следовательно, в отличие от линзы, для каждой длины волны зонная пластинка имеет несколько фокусов. Это обстоятельство аналогично наличию максимумов различных порядков у дифракционных решеток. Фокусирующее действие зонной пластинки будет иметь место и тогда, когда лучи света падают на пластинку под небольшим углом. Следовательно, с помощью зонной пластинки можно получить изображение протяженных источников или предметов.
При прохождении света через амплитудную зонную пластинку половина световой энергии падающей волны теряется из-за поглощения в непрозрачных областях пластинки. Для того, чтобы избежать этих потерь и увеличить эффективность сбора световой энергии в точке Р, используют фазовую зонную пластинку (ФЗП). Она изменяет фазу колебаний от всех четных зон на п. При этом амплитуда результирующего колебания по сравнению с амплитудной зонной пластинкой увеличивается в точке Р в два раза, а интенсивность, соответственно, в четыре (рис.3).
Р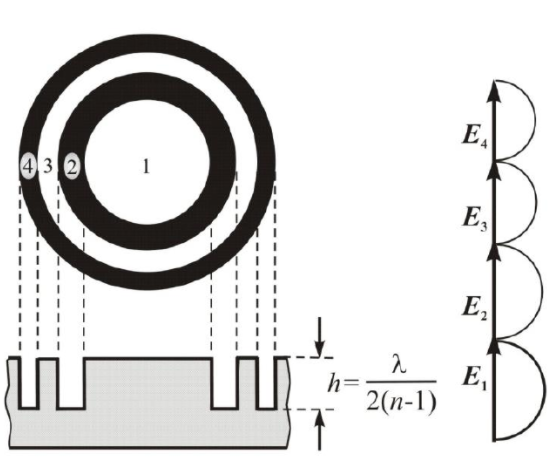 ис.3. Профиль двухуровневой фазовой ис.3. Профиль двухуровневой фазовой
зонной пластинки.
Чтобы изменить фазу волны на , следует изменить оптический путь на /2. Для этого толщину стеклянной пластинки в местах, соответствующих четным зонам Френеля, нужно уменьшить или увеличить на величину h, равную:
h /2(n 1)
Сечение такой пластинки показано на рис. 3 Для видимого света величина h приблизительно равна 0,5 мкм.
Двухуровневая ФЗП способна сконцентрировать в точке Р до 40% световой энергии, падающей на нее. Еще больше увеличить амплитуду колебаний в точке Р можно с помощью трехуровневой ФЗП (рис.4).
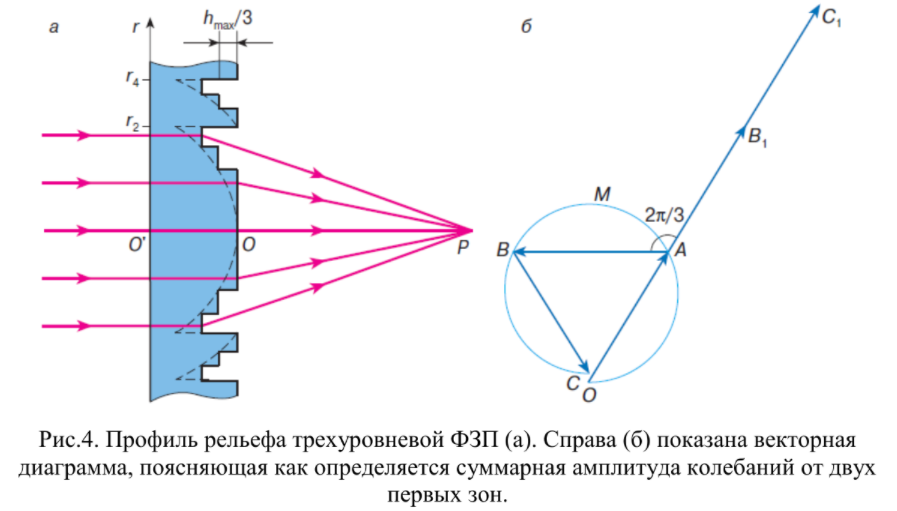
Для создания такой ФЗП поверхность двух соседних зон, например, 1 и 2, разбивается на три кольцевые части равной площади (очевидно, что они будут отличаться по ширине). Вклад от каждой части на векторной диаграмме изобразится векторами ОА, АВ и ВС, а их сумма равна нулю (рис.4б). Чтобы сделать модуль суммы этих векторов максимальным, необходимо, очевидно, повернуть вектор АВ на угол 2/3, а вектор ВС – на 4/3. Этого можно достичь уменьшением фазы волн от этих участков. Для этого необходимо вторую кольцевую часть углубить на величину hmax/3, а третью – на 2hmax/3. Профиль такой ФЗП показан на рис.4а.
Амплитуда колебаний в точке Р, создаваемая трехуровневой ФЗП, в 3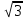 /4 раза больше амплитуды, создаваемой двухуровневой ФЗП, а интенсивность, соответственно, в 27/16 раз (см. рис.3 и 4). /4 раза больше амплитуды, создаваемой двухуровневой ФЗП, а интенсивность, соответственно, в 27/16 раз (см. рис.3 и 4).
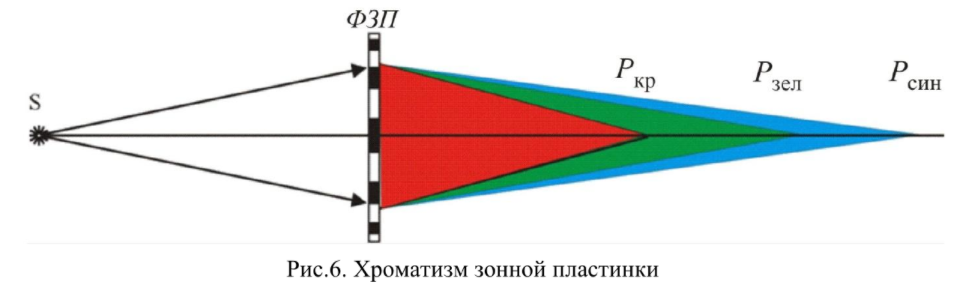
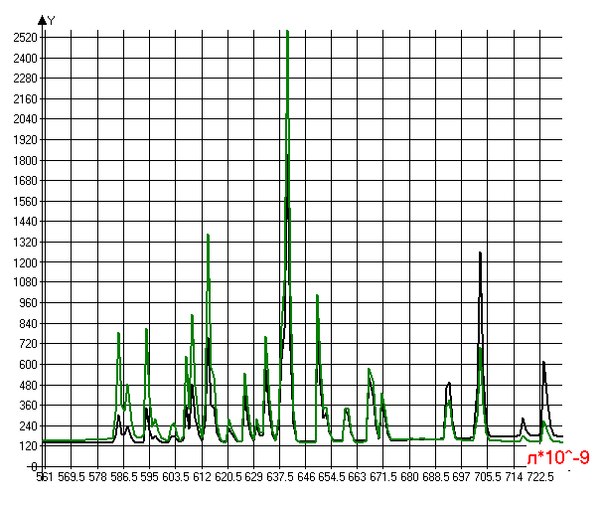
Если призма разлагает немонохроматический свет в спектр в направлении, перпендикулярном к направлению распространения волны, то ФЗП разлагает свет в спектр вдоль направления распространения волны.
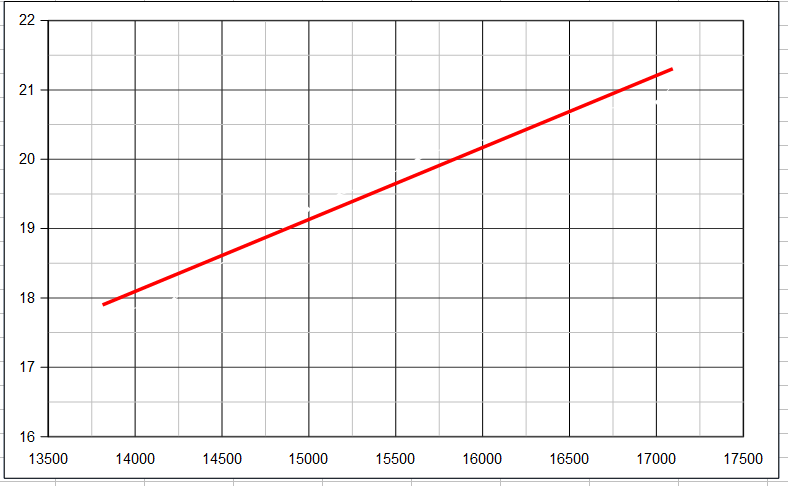
График зависимости расстояния между источником и ФЗП (а) и расстояния между входным отверстием оптического волокна и ФЗП (b) от 107/. По вертикали представлена величина ab/(a+b), см.
|
|
|
 Скачать 3.05 Mb.
Скачать 3.05 Mb.