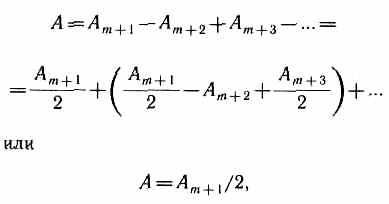|
|
Дифракція світла. Дифракція світла п ринцип ГюйгенсаФренеля
Дифракція світла
П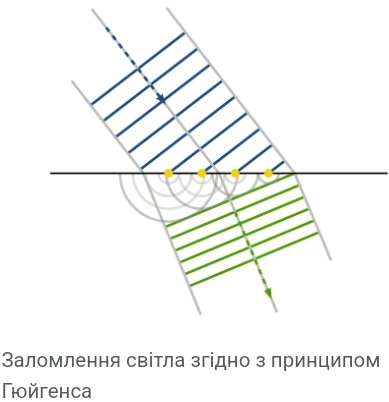
ринцип Гюйгенса-Френеля — фізичний принцип, згідно з яким будь-яка точка простору, якої досягла хвиля, є джерелом вторинних хвиль, що розповсюджуються у всіх напрямках
Принцип Гюйгенса пояснює багато оптичних явищ, серед яких прямолінійне розповсюдження світла, заломлення, дифракція.
Випромінені кожною точкою простору хвилі додаються, підсилюючи одна одну в певних напрямках, взаємно гасячись у інших, у залежності від різниці фаз коливань.
Принцип Гюйгенса є наближенням, яке при певному вмінні можна використовувати для розгляду оптичних явищ замість розв’язування часткових диференціальних рівнянь.
За хвильовою теорією Гюйгенса світло — це хвилі, що поширюються у світовому ефірі — гіпотетичному пружному середовищі, який заповнює увесь простір і проникає всередину всіх тіл. Основний недолік теорії полягав у тому, що вона ґрунтувалась на уявленні про світло як про механічну поперечну хвилю, для поширення якого необхідна наявність певного середовища – ефіру. Френель в 1815 році доповнив принцип Гюйгенса, що дозволило розглядати дифракцію за допомогою принципа Гюйгенса-Френеля.
Метод зон Френеля
Френель запропонував оригінальний метод розбиття хвильової поверхні S на зони, що дозволив сильно спростити вирішення завдань, - метод зон Френеля
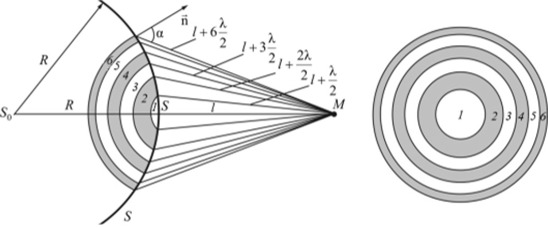
Загальна кількість зон Френеля, що вміщується на частини сфери, зверненої в бік точки М, дуже велике: при ^ = 5-1 (Г 7 м = 500 нм, Я = / = 0,1 м число зон 3 * 10 5 , а радіус першої зони г - 0,16 мм.
Звідси випливає, що кути між нормаллю до зони і напрямком на точку М у сусідніх зон приблизно рівні, т. Е. Що амплітуди хвиль , що приходять в точку М від сусідніх зон , приблизно рівні.
Так як площі сусідніх зон однакові, то вирази в дужках
дорівнюють нулю, значить, результуюча амплітуда
Інтенсивність випромінювання J А 2 .
Таким чином, результуюча амплітуда, створювана в деякій точці М всієї сферичної поверхнею , дорівнює половині амплітуди, створюваної однієї лише центральною зоною, а інтенсивність J = J y l 4.
Так як радіус центральної зони малий (/ * i
0,16 мм), можна вважати, що світло від точки Р до точки М поширюється прямолінійно , уздовж математичної лінії, званої світловим променем.
Якщо на шляху хвилі поставити непрозорий екран з отвором, залишає відкритою тільки центральну зону Френеля, то амплітуда в точці М буде дорівнює А г Відповідно, інтенсивність в точці М буде в 4 рази більше, ніж за відсутності екрану (т. К. J = 4У ,). Інтенсивність світла збільшується, якщо закрити всі парні зони.
Таким чином, принцип Гюйгенса - Френеля дозволяє пояснити прямолінійне поширення світла в однорідному середовищі.
Правомірність розподілу хвильового фронту на зони Френеля підтверджена експериментально. Для цього використовуються зонні пластинки - система чергуються прозорих і непрозорих кілець.
Досвід підтверджує, що за допомогою зонних пластинок можна збільшити освітленість в точці М подібно збирає лінзі.
Дифракція сферичних хвиль на круглому отворі
1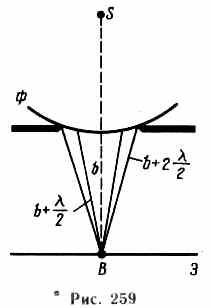 . Дифракція на круглому отворі. Сферична хвиля, що розповсюджується з точкового джерела 5, зустрічає на своєму шляху екран з круглим отвором. Дифракційну картину спостерігаємо на екрані (Е) в точці В, що лежить на лінії, що з'єднує S з центром отвору (рис. 259). Екран паралельний площині отвер-сті і знаходиться від нього на відстані b. Розіб'ємо відкриту частину хвильової по-поверхні Ф на зони Френеля. Вид диф-ракціонной картини залежить від числа зон Френеля, укладаються в отворі. Амплітуда результуючого коливання, що збуджується в точці В усіма зонами (див. (177,1) і (177.6)),
де знак плюс відповідає непарних т і мінус - парних від.
Коли отвір відкриває непарне число зон Френеля, то амплітуда (інтенсивність-ність) в точці В буде більше, ніж при
вільному поширенні хвилі, якщо парне, то амплітуда (інтенсивність) бу-дет дорівнює нулю. Якщо в отвір уклади-ється одна зона Френеля, то в точці В амплітуда А = А1, т. Е. Вдвічі більше, ніж за відсутності непрозорого екрану з отвором (див. §177). Інтенсивність світла більше відповідно в чотири ра-за. Якщо в отворі укладаються дві зони Френеля, то їх дії в точці В практично знищать один одного через інтерференції. Таким чином, діфрак-Ціон картина від круглого отвору поблизу точки В буде мати вигляд чергую-трудящих темних і світлих кілець з центрами в точці В (якщо т парне, то в центрі буде темне кільце, якщо т непарне - то світле кільце), причому інтенсивність максимумів зменшується з відстанню від центру картини.
Розрахунок амплітуди результуючого коливання на внеосевой ділянках екрану більш складний, тому що відповідні їм зони Френеля частково перекриваються непрозорим екраном. Якщо отвір освітлювали не монохроматичним, а бе-лим світлом, то кільця пофарбовані.
Ч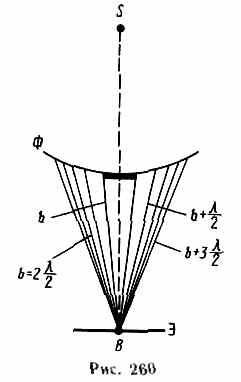 исло зон Френеля, укладаються в отворі, залежить від його діаметра. Якщо він великий, то Am <<="" p=""> і під час відсутності круглого отвору, прямо-лінійно.
2. Дифракція на диску. Сферична хвиля, що розповсюджується від точкового джерела 5, зустрічає на своєму шляху диск. Дифракційну картину спостерігаємо на екрані (Е) в точці В, що лежить на лінії, що з'єднує S з центром диска (рис. 260). В даному випадку закритий диском ділянку фронту хвилі треба виключним видом-чить з розгляду і зони Френеля будувати починаючи з країв диска. Нехай диск закриває m перших зон Френеля. Тоді амплітуда результуючого коливання в точці В дорівнює так як висловлювання, які стоять в дужках, дорівнюють нулю. Отже, в точці В завжди спостерігається інтерференційний максимум (світла пляма), відповідаю-щий половині дії першої відкритої зони Френеля. Центральний максимум ок-Ружені концентричними з ним темними і світлими кільцями, а інтенсивність максимумів зменшується з відстанню від центру картини.
Зі збільшенням радіусу диска перша відкрита зона Френеля віддаляється від точ-ки В і збільшується кут jm (див. Рис. 258) між нормаллю до поверхні цієї зони і напрямком на точку В. У ре-док інтенсивність центрального мак-симум зі збільшенням розмірів диска зменшується. При великих розмірах диска за ним спостерігається тінь, поблизу кордонів якої має місце вельми слабка дифракційна картина. В даному випадку дифракцией світла можна знехтувати і вважати світло поширюється пря-молінейно.
Відзначимо, що дифракція на круглому від-верст і дифракція на диску вперше розглянуті Френелем.
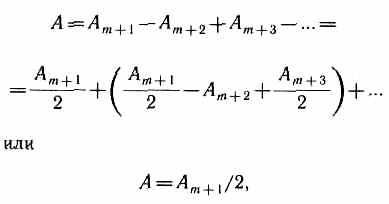
Дифракція сферичних хвиль на непрозорому диску
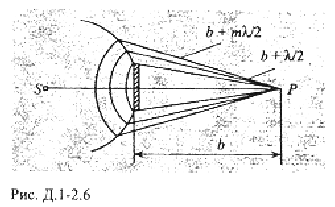
З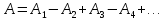
астосуємо метод зон Френеля до дифракції сферичних хвиль на круглому непрозорому диску. Сферична монохроматична хвиля поширюється від точкового джерела світла S, і на її шляху розміщено круглий непрозорий диск (див. рис.). Необхідно визначити амплітуду світлової хвилі, яка досягає точки P, розміщеної на одній прямій, що сполучає джерело і точку Р, і проходить через вершину фронту. Усі відстані і позначення залишаються такими самими, як у попередньому випадку. Однак закриту диском частину фронту не розглядають , а розглядають тільки зони Френеля на відкритій частині фронту. Амплітуда результуючої хвилі в точці Р визначається за формулою:
Дифракція плоских хвиль на щілині
З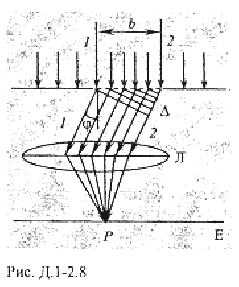
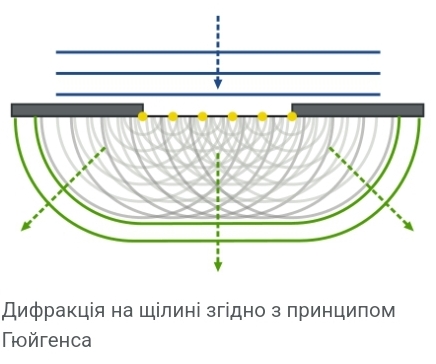
астосовуємо метод зон Френеля до дифракції плоских хвиль на щілині.На довгу прямокутну прямокутну щілину завширшки b падає нормально паралельний пучок монохроматичного світла
З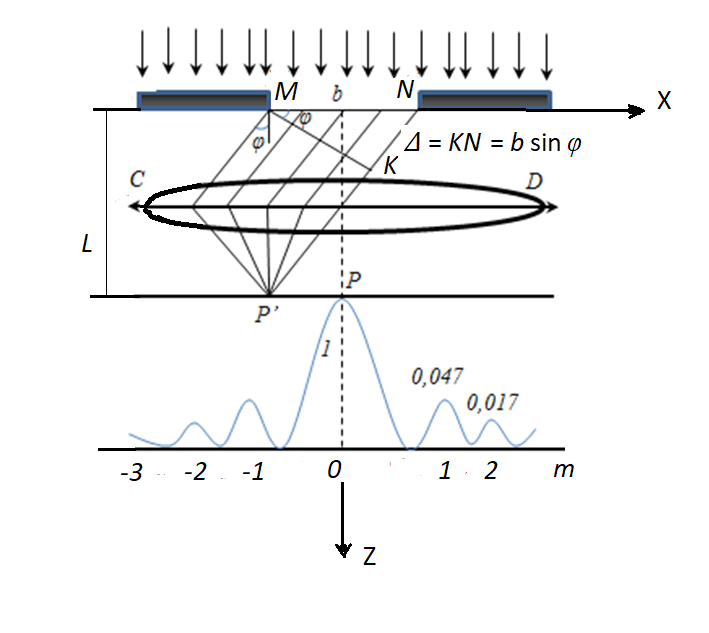
а принципом Гюйгенса-Френеля точки щілини є вторинними джерелами сферичних хвиль, тому за щілиною промені поширюються в усіх напрямках під різними кутами до попереднього поширення світла. На екрані Е спостерігається система інтерференційних максимумів і мінімумів. Розглянемо один із напрямів, що задається кутом φ, який називається кутом дифракції світла. Паралельно промені, які поширюються щілиною під кутом φ, який називається кутом дифракції світла збираються лінзою Л на екрані Е в точці Р. Оптична різниця ходу  між крайніми променями 1 і 2 визначається за формулою:
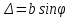
П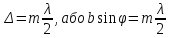
оділимо щілину на зони Френеля. Якщо на оптичній різниці ходу укладається ціла кількість зон:
Якщо кількість зон Френеля дорівнює парному числу, - у точці Р спостерігається мінімум інтерференції.
Я
кщо кількість зон Френеля дорівнює непарному числу, - у точці Р спостерігається максимум інтерференції.
Практичне використання дифракції. Дифракційна решітка
Ш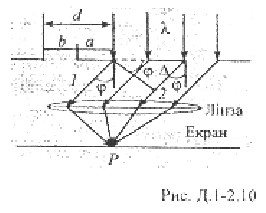
ироке практичне застосування має не дифракція світла на одній щілині, а дифракція на дифракційній рещітці.
Дифракційна решітка являє собою сукупність великої кількості щілин поділеної непрозорими для світла проміжками. Дифракційну решітку виготовляють так: на скляній поверхні алмазним різцем наносять дуже багато прямих штрихів. Подряпані місця розсіюють світло, а непошкодженні частини поверхні пропускають світло як щілини. Позначимо ширину щілини b, а ширину непрозорого проміжку між сусідніми щілинами - a.
Формула d sinφ = kλ, називається умовою головних максимумів дифракційної решітки.
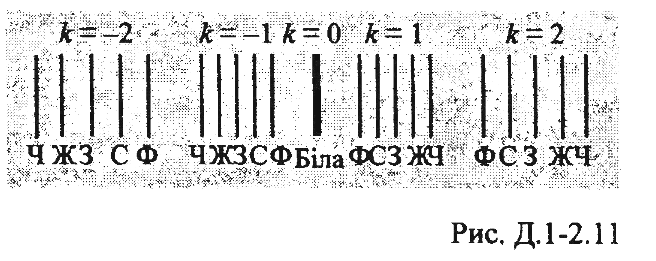
Якщо дифракційна решітка освітлюється білим світлом, то для різних значень довжин хвиль  положення всіх головних максимумів (max), окрім центрального, різні. Тому центральний максимум має вигляд білої смуги, а решта - різноколірних смуг, які називаються дифракційними спектрами першого, другого і наступних порядків. Центральний максимум - один, а максимумів інших порядків - два, і вони розміщуються на екрані симетрично відносно нульового (див. рис.). У межах кожного порядку колір змінюється від фіолетового (біля внутрішнього краю) до червоного (біля зовнішнього краю).
Основними характеристиками будь-якого спектрального приладу є кутова дисперсія і роздільна здатність . Найкращі дифракційні решітки мають до 1200 штрихів на 1 мм.
Окрім прозорих решіток бувають ще відбивальні решіткі, при виготовлені яких штрихи наносяться алмазним різцем на поверхню металевого дзеркала |
|
|
Скачать 2.11 Mb.