Решение задачи по теоретической механики. 1 задача техмех. Тсіндірме жазбалар пояснительная записка к курсовой работе по дисциплине Прикладная механика
 Скачать 247.87 Kb.
|
 Қазақстан Республикасының білім және ғылым министрлігіМинистерство образования и науки Республики Казахстан Северо – Казахстанский государственный университет имени М. Козыбаева Манаш Қозыбаев атындағы Солтүстік Қазақстан мемлекеттік университеті Инженерлік және сандық технологиялар факультеті Факультет инженерии и цифровых технологий «Көлік және машина жасау» кафедрасы Кафедра «Транспорт и машиностроение» ТҮСІНДІРМЕ ЖАЗБАЛАР ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по дисциплине «Прикладная механика» 5В0713 КРД14 000.000.000 ПЗ Орындады: Выполнил: _Клименов_____ Тр-18 тобының студенті Студент гр. Тр-18 Тексерді: Проверил: __________ Дерман А.Л. «КжМЖ» кафедрасының аға оқытушысы ст. преп. кафедры «ТиМ» Комиссия мүшелері: Члены комиссии: _______________ _______________ Петропавл қ., 2019 ж. г. Петропавловск, 2019 г.  Содержание
Введение  Из предисловия к учебнику А. П. Маркеева «Теоретическая механика»: «Как фундаментальная наука теоретическая механика была и остаётся не только одной из дисциплин, дающей углублённые знания о природе. Она также служит средством воспитания у будущих специалистов необходимых творческих навыков к построению математических моделей, происходящих в природе и технике процессов, к выработке способностей к научным обобщениям и выводам». В физике под «теоретической механикой» подразумевается часть теоретической физики, изучающая математические методы классической механики, альтернативные прямому применению законов Ньютона (так называемая аналитическая механика). Сюда входят, в частности, методы, основанные на уравнениях Лагранжа, принципе наименьшего действия, уравнении Гамильтона — Якоби и др. В технических науках под «теоретической механикой» подразумевается набор физико-математических методов, облегчающих расчёты механизмов, сооружений, летательных аппаратов и т. п. (так называемая прикладная механика или строительная механика) . Практически всегда эти методы выводятся из законов классической механики — в основном, из законов Ньютона, хотя в некоторых технических задачах оказываются полезными некоторые из методов аналитической механики. Теоретическая механика опирается на некоторое число законов, установленных в опытной механике, принимаемых за истины, не требующих доказательств — аксиомы. Эти аксиомы заменяют собой индуктивные истины опытной механики. Теоретическая механика имеет дедуктивный характер. Опираясь на аксиомы как на известный и проверенный практикой и экспериментом фундамент, теоретическая механика возводит своё здание при помощи строгих математических выводов. Теоретическая механика как часть естествознания, использующая математические методы, имеет дело не с самими реальными материальными объектами, а с их моделями. Такими моделями, изучаемыми в теоретической механике, являются: материальные точки и системы материальных точек, абсолютно твёрдые тела и системы твёрдых тел, деформируемые сплошные среды.  Задание №1. Темы «Основные понятия и аксиомы статики», «Плоская система сходящихся сил»Пример 1.1 Определить реакции стержней, удерживающих грузы F1=0.3 кН и F2= 0.8 кН (рис. 1.1). Массой стержней пренебречь. Рассматриваем равновесие шарнира В (рис. 1, а).  Рисунок 1.1 – Заданная схема стержневой системы Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. 1.2).   Рисунок 1.2 – Расчётная схема стержневой системы 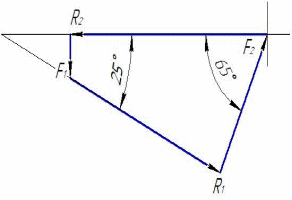 Рисунок 1.3 – Расчётная схема стержневой системы Выбираем систему координат и доставляем уравнения равновесия для системы сил, действующих на шарнир В.  (1) (2)Определяем реакции стержней R1 и R2, решая уравнения (1), (2). Из уравнения (1)  Подставляем найденное значение R1 в уравнение (2) и получаем 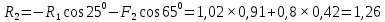 Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное – следует направить реакцию R2 в противоположную сторону, т.е. к шарниру В (на рис.1.2 добавлено истинное направление реакции R2). Проверяем правильность полученных результатов, решая задачу графически (рис. 1.3). Полученная система сил (рис. 1.2) находиться в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым. Графическое решение подтверждает правильность первого решения.  Пример 1.2. Определить реакции стержней, удерживающих грузы F1=0.2 кН и F2= 0.5 кН (рис. 1.1). Массой стержней пренебречь. Рассматриваем равновесие шарнира В (рис. 1, а). Рисунок 1.4 – Заданная схема стержневой системы Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. 1.2).  Рисунок 1.5 – Расчётная схема стержневой системы 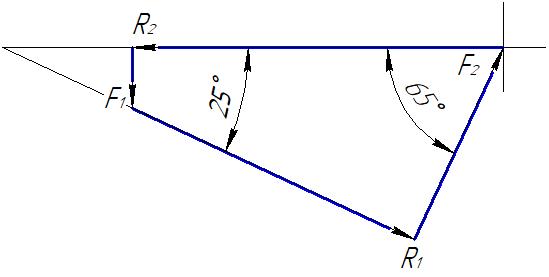 Рисунок 1.6 – Расчётная схема стержневой системы  Выбираем систему координат и доставляем уравнения равновесия для системы сил, действующих на шарнир В. (1) (2)Определяем реакции стержней R1 и R2, решая уравнения (1), (2). Из уравнения (1)  Подставляем найденное значение R1 в уравнение (2) и получаем 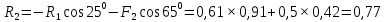 Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное – следует направить реакцию R2 в противоположную сторону, т.е. к шарниру В (на рис.1.5 добавлено истинное направление реакции R2). Проверяем правильность полученных результатов, решая задачу графически (рис. 1.6). Полученная система сил (рис. 1.5) находиться в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым. Графическое решение подтверждает правильность первого решения.  Список используемой литературы А.А. Яблонский, В.М. Никифоров «Курс теоретической механики», М.: «Лань», 2001. Под ред. А.А. Яблонского «Сборник заданий для курсовых работ по теоретической механике», М.: «ИНТЕГРАЛ-ПРЕСС», 2006. В.Г. Жуков «Механика. Сопротивление материалов: Учебное пособие», СПб.: Издательство «Лань», 2012. А.И. Столярчук «Техническая механика. Контрольные задания», М.: «Высшая школа», 1986. А.Д. Полянин, В.Д. Полянин, В.А. Попов, Б.В. Путятин, В.М. Сафрай, А.И. Черноуцан «Краткий справочник для инженеров и студентов: Высшая математика. Физика. Теоретическая механика. Сопротивление материалов», М.: «Международная программа образования», 1996.  |