теор мех. теормех 8 билет. 1 учебный вопрос Условия равновесия системы сходящихся сил
 Скачать 95.25 Kb.
|
|
1 учебный вопрос Условия равновесия системы сходящихся сил Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпасть с началом первой силы. Такой силовой многоугольник называют замкнутым (рис. 15). Получено условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил. 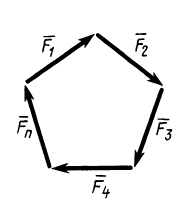 Рис. 15 Для определения неизвестных сил при равновесии более предпочтительным является использование условий равновесия системы сходящихся сил в аналитической форме. Так как при равновесии системы сходящихся сил равнодействующая сила должна быть равна нулю (силовой многоугольник замкнут), то из этого следует, что равно нулю подкоренное выражение в (3), состоящее из суммы положительных величин. Таким образом, равны нулю квадраты каждой из величин подкоренного выражения, а следовательно, равны нулю и сами величины. Получаем условия равновесия пространственной системы сходящихся сил в аналитической форме: 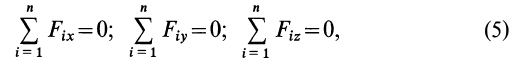 т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю. В случае плоской системы сходящихся сил одну из осей координат, обычно 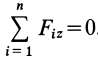 , выбирают перпендикулярной силам, а две другие оси—соответственно в плоскости сил. Тогда третье условие из (5) превратится в тождество  . Отбрасывая его, получаем т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю. Проецирование силы на оси координат Если дана сила 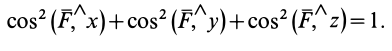 , то ее проекции на прямоугольные оси координат вычисляются по формулам где  — единичные векторы, направленные по осям координат. Косинусы углов силы с осями координат удовлетворяют условию Из трех углов независимыми являются только два. 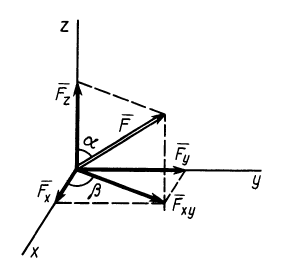 Рис. 16 При проецировании силы на прямоугольные оси координат целесообразно использовать тоже два угла. Для этого предварительно силу разлагают на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-либо оси координат, например , а другая находится в координатной плоскости двух других осей, в нашем случае — координатной плоскости  (рис. 16). Получаем Проецируя векторы векторного равенства на координатные оси, имеем 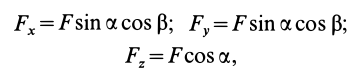 так как  При проецировании использованы только два угла:  и  .Векторные величины  ,  ,  называются составляющими силы  по осям координат. Скалярные величины , , являются проекциями силы на оси координат. Таким образом, силу на оси координат проецируют обычно в два приема. Сначала ее проецируют на одну из осей и на координатную плоскость двух других осей. Проекция силы на плоскость является вектором. Этот вектор затем проецируют на оси координат, расположенные в плоскости.2 учебный вопрос: ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫТеорема гласит: изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.Рассмотрим движение произвольной точки системы из первого положения во второе:  где Fke — внешние силы, действующие на систему, Fki — внутренние силы системы. Умножим обе части уравнения скалярно на дифференциал радиуса-вектора drk тогда 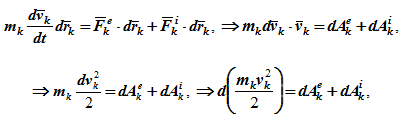 или dTk = dAke + dAki , (1.1) где Tk — кинетическая энергия точки; далее получим 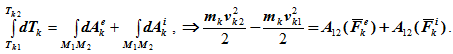 Просуммируем по всем точкам системы 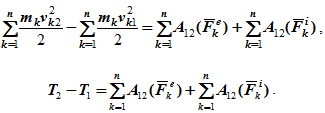 То есть, изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении. Если в формуле (1.1) обе части уравнения разделить на dt, то можно записать теорему об изменении кинетической энергии системы в дифференциальной форме: производная по времени от кинетической энергии механической системы равна сумме мощностей внешних и внутренних сил, действующих на систему. dTk / dt = dAke / dt + dAki / dt dTk / dt = Nke + Nki. Суммируя по всем точкам системы, получим dT / dt = ∑Nke + ∑Nki. |