Задание 1 Плоская система сходящихся сил. Задание 1 Плоская система сходящихся сил. Определение равнодействующей геометрическим способом

• Название: Задание 1 Плоская система сходящихся сил. Определение равнодействующей геометрическим способом
• Дата: 03.10.2022
• Размер: 69.54 Kb.
• Имя файла: Задание 1 Плоская система сходящихся сил.docx
• Тип: Задача; #710569

Задание 1
Плоская система сходящихся сил. Определение равнодействующей геометрическим способом

Знать геометрический способ определения равнодействующей системы сил, условия равновесия плоской системы сходящихся сил.

Уметь определять равнодействующую, решать задачи на равновесие в геометрической форме.
Задача №1.

Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.). Изобразить систему сил, действующих на шарнир .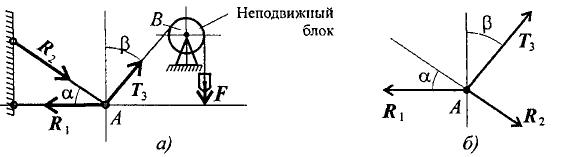



Рис. 1

Решение:

1. 
   Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.а).
   
2. 
   Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки . Неподвижный блок с действующими на него силами не рассматриваем.
   
3. 
   Убираем стержень 1. точка поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.
   
4. 
   Убираем стержень 2, точка поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
   
5. 
   Канат тянет вправо.
   
6. 
   Освобождаемся от связей (рис. 1.б).
   

Задача №2.

Шар подвешен на нити и опирается на стену (рис. 2 а).

Определить реакции нити и гладкой опоры (стенки).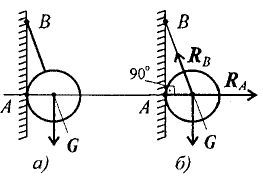



Рис.2

Решение:

1. 
   Реакция нити — вдоль нити к точке вверх (рис. 2 б).
   
2. 
   Реакция гладкой опоры (стенки) — по нормали от поверхности опоры.
   

Плоская система сходящихся сил. Определение равнодействующей аналитическим способом

Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в аналитической форме.

Уметь определять проекции силы на две взаимно перпендикулярные оси, решать задачи на равновесие в аналитической форме.

Решение задач на равновесие геометрическим способом

Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).

Порядок решения задач:

1. 
   Определить возможное направление реакций связей.
   
2. 
   Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.)
   
3. 
   Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
   
4. 
   Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
   

Задача №3.

Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 3 а).

Решение:

Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 3 а).

Определяем возможные направления реакций связей «жесткие стержни».



Рис. 3

Усилия направлены вдоль стержней.

Освободим точку от связей, заменив действие связей их реакциями (рис. 3 б).

Система находится в равновесии. Построим треугольник сил.

Построение начнем с известной силы, вычертив вектор в некотором масштабе.

Из концов вектора проводим линии, параллельные реакциям и .

Пересекаясь, линии создадут треугольник (рис. 3 в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.

Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная





Для данного случая: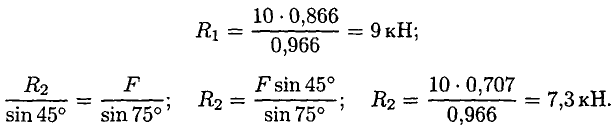





Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
Задача №4.

Груз подвешен на стержнях и канатах и находится в равновесии.

Определить усилия в стержнях (рис. 4 а).

Решение:



Рис. 4

Нанесем на схему возможные направления усилий, приложенных в точке . Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки к точке .

Груз находится в равновесии, следовательно, в равновесии находится точка , в которой пересекаются три силы.

Освободим точку от связей и рассмотрим ее равновесие (рис. 4 б).

Замечание. Рассмотрим только силы, приложенные к точке . Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: .

Строим треугольник для сил, приложенных в точке , начиная с известной силы . Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке .

Образовался прямоугольный треугольник (рис. 4 в).

Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике:



Замечание. При равновесии векторы сил в треугольнике направлены один за другим (обходим треугольник по часовой стрелке).

Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 4 а.

Направления совпали, следовательно, направления реакций определены верно.

Теорема о трех непараллельных силах

Теорема. Если свободное абсолютно твердое тело находится в равновесии под действием трех непараллельных сил, лежащих на одной плоскости, то линии действия этих сил пересекаются в одной точке.
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется связью? В чём заключается аксиома освобождаемости от связей?

2. Перечислите основные виды связей и возникающие в них реакции.

3. Что называется равнодействующей и главным вектором системы сил?

4. Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника?