тер мех. Тер мех 5-6. Теорема. Если свободное абсолютно твердое тело находится в равновесии под действием трех непараллельных сил, лежащих на одной плоскости, то линии действия этих сил пересекаются в одной точке. Доказательство
 Скачать 74.06 Kb. Скачать 74.06 Kb.
|
|
Теорема о трёх силах. Теорема. Если свободное абсолютно твердое тело находится в равновесии под действием трех непараллельных сил, лежащих на одной плоскости, то линии действия этих сил пересекаются в одной точке. Доказательство. Пусть на абсолютно твердое тело, находящееся в равновесии действуют три непараллельные силы F⃗ 1�→1, F⃗ 2�→2 и F⃗ 3�→3 как указано на рис. С.17а. 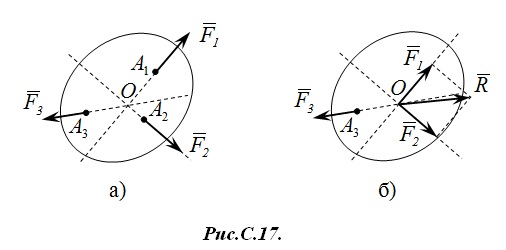
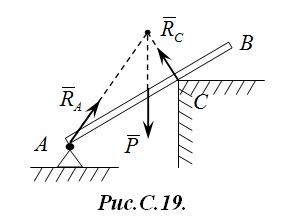
В соответствие со следствием аксиомы №2 силы F⃗ 1�→1 и F⃗ 2�→2 являются скользящими векторами и их можно перенести вдоль линии действия в точку их пересечения O�. Теперь силы F⃗ 1�→1 и F⃗ 2�→2 приложены к одной точке и в соответствие с аксиомой №3 их можно сложить R⃗ =F⃗ 1+F⃗ 2�→=�→1+�→2. Теперь, как следует из рис.С.17б тело находится в равновесии под действием системы состоящей из двух сил {F⃗ 3,R⃗ }{�→3,�→} и в соответствие с аксиомой №1 эти силы действуют вдоль одной прямой. Следовательно, линии действия сил F⃗ 1�→1 , F⃗ 2�→2 и F⃗ 3�→3 имеют общую точку пересечения, точку O� и образуют сходящуюся систему сил. Пример. Стержень AB�� в точке A� опирается на неподвижный шарнир, а в точке C� на выступ (рис.С.18). 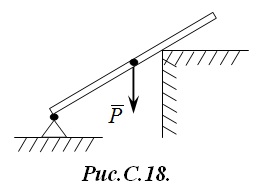 Определить направления реакций в опорах (точках A� и C�). Решение. Решение приведено графически на рис.С.19.
 Момент силы относительно центра Моментом силы F относительно центра О называется приложенный в центре О вектор mn(F), модуль которого равен F И и который направлен в ту сторону, откуда вращение видно против хода часовой стрелки. Момент m0(F) равен векторному произведению радиус-вектора г, проведенного из центра О в точку приложения силы Л, на саму эту силу. 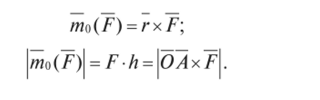 Отметим следующие свойства момента силы: • момент силы не изменится, если силу перенести вдоль линии ее действия в другую точку тела; • момент силы равен 0 или когда сила равна 0, или когда линия действия силы проходит через центр О (плечо h = 0) |
