ЛАБА 6 ОТЧЕТ. Динамические эконометрические модели
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
КАЗАНСКИЙ ИННОВАЦИОННЫЙ УНИВЕРСИТЕТ ИМ. В.Г. ТИМИРЯСОВА (ИЭУП) Кафедра высшей математики ЛАБОРАТОРНАЯ РАБОТА №6 ПО ЭКОНОМЕТРИКЕ Тема: ДИНАМИЧЕСКИЕ ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ Вариант 25 Выполнил: студент группы №181 факультета Экономики Разяпова Гульназ Маратовна зачетная книжка № 18-1-25 Руководитель: проф. (доц.; ст. преп.; асс.) Кадочникова Е.И. Город обучения – 2020 г. ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ №6 Задание. Имеются квартальные данные о деятельности ПАО «Оргсинтез», г. Казань, с 2012 по 2018 годы. Зависимая переменная Y – чистая рентабельность активов, регрессор Х – доля кредиторской задолженности в заемном капитале, %.
Необходимо: оценить параметры модели с распределенным лагом с длиной лага не более 3, используя метод Койка; оценить параметры модели с распределенным лагом с длиной лага не более 3 и степени аппроксимирующего полинома не более 3, используя метод Алмон; сравнить результаты, полученные в пунктах 1 и 2. Решение. Комментарий: Модель авторегрессии и распределённого лага (ADL –модель, англ. autoregressive distributed lags) – модель временного ряда, в которой текущие значения ряда зависят как от прошлых значений этого ряда, так и от текущих и прошлых значений других временных рядов. Модель ADL (0,q) – это модель распределённого лага DL (q). Иногда используют обозначение ADL(p,q;k), где k – количество экзогенных переменных, q – количество лагов. Наложение ограничений на коэффициенты этой модели приводит к тем или иным вариациям. Модели распределённого лага (DL-модели) позволяют учесть запаздывающее влияние факторов (наряду с текущим). Коэффициенты DL-модели называют промежуточными мультипликаторами. Однако в каждый момент времени оказывают влияние несколько лаговых значений фактора, поэтому в долгосрочной перспективе коэффициент влияния фактора (долгосрочный мультипликатор) равен сумме промежуточных мультипликаторов. Добавление к модели распределённого лага авторегрессионной части позволяет учесть кроме прямого влияния и опосредованное – через влияние прошлых значений зависимой переменной на её же будущие значения. Знаменатель в формуле долгосрочного мультипликатора и учитывает авторегрессионное увеличение мультипликативного эффекта. В нашем случае предполагается использовать модель ADL(0,q;1), а для ее оценки – специальные приемы: метод Койка и метод Алмон. Метод Койка Сформируем лаговую переменную 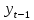 , переместив на 1 месяц вниз уровни , переместив на 1 месяц вниз уровни 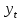 , первое наблюдение , первое наблюдение 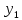 отбрасывается. отбрасывается.Чтобы оценить множественную линейную регрессию 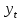 на на 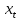 и и 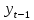 в MS Excel с помощью инструмента Регрессия надстройки Пакет анализа в главном меню программы MS Excel на вкладке Данные (в верхней строке) выберем опцию Анализ данных, а в списке Инструментов анализа выберем инструмент Регрессия. В качестве регрессанта выберем переменную в MS Excel с помощью инструмента Регрессия надстройки Пакет анализа в главном меню программы MS Excel на вкладке Данные (в верхней строке) выберем опцию Анализ данных, а в списке Инструментов анализа выберем инструмент Регрессия. В качестве регрессанта выберем переменную 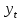 – чистая рентабельность активов, а в качестве регрессоров укажем диапазон переменных – чистая рентабельность активов, а в качестве регрессоров укажем диапазон переменных 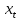 – доля кредиторской задолженности в заемном капитале, – доля кредиторской задолженности в заемном капитале, 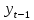 – лаговая переменная для чистой рентабельности активов. Диапазон значений начинаем выделять с третьей строки в MS Excel, не отмечаем «галочку» в опции Метки (рис. 1). – лаговая переменная для чистой рентабельности активов. Диапазон значений начинаем выделять с третьей строки в MS Excel, не отмечаем «галочку» в опции Метки (рис. 1).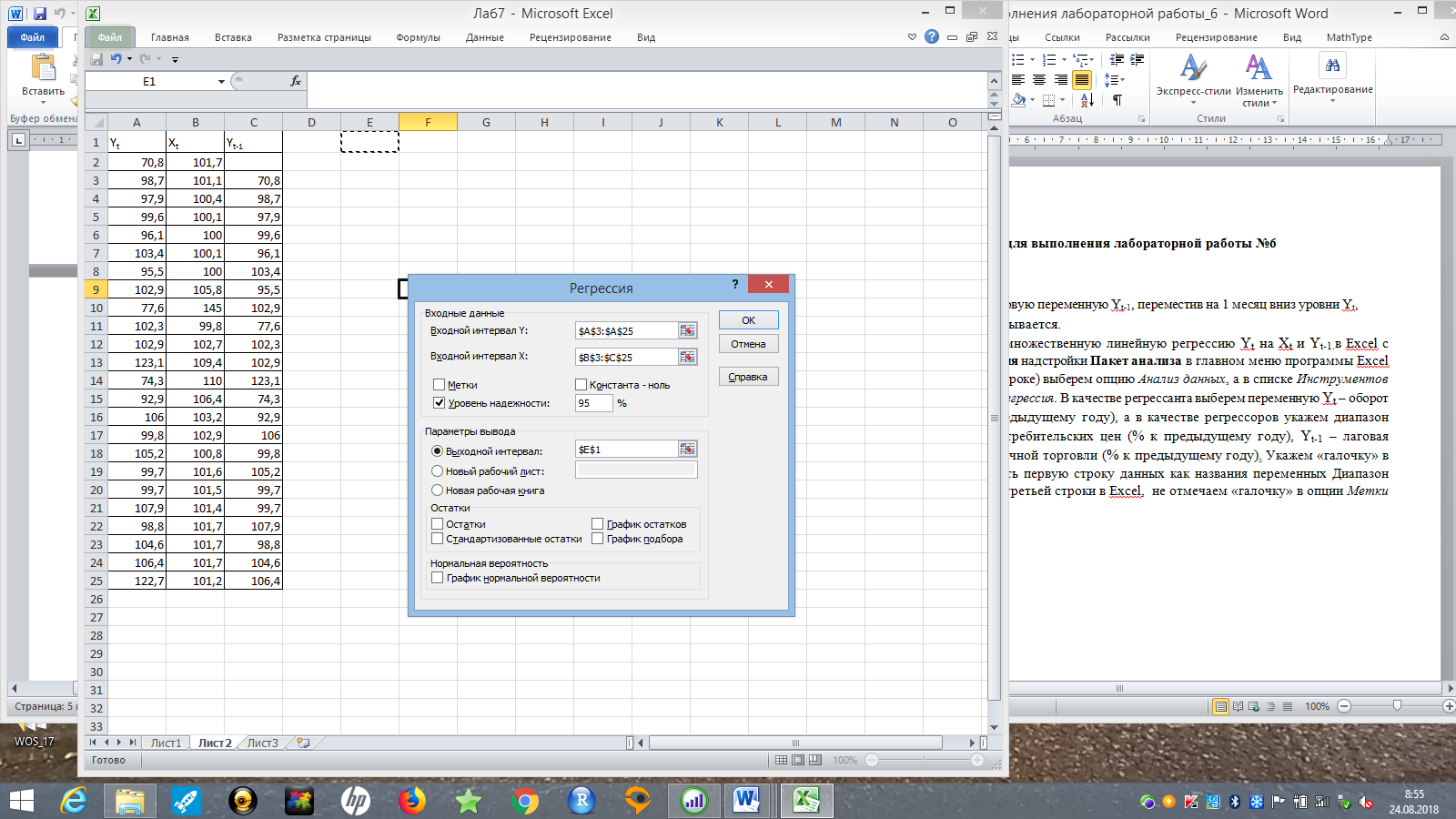 Рис. 1. Окно параметров регрессии с введенными значениями в MS Excel Далее, нажав на кнопку Ок, получаем результаты (рис. 2). 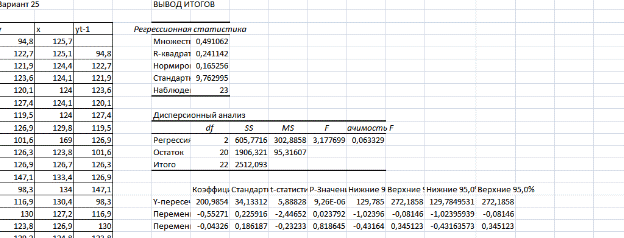 Рис. 2. Вывод результатов оценивания регрессии в MS Excel В нижней подтаблице в столбце «Коэффициенты» содержатся коэффициенты регрессии для регрессоров 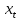 и и 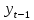 , равные -0,55 и -0,043 соответственно, а также свободный коэффициент, равный 200,98 на пересечении со строкой «Y-пересечение». , равные -0,55 и -0,043 соответственно, а также свободный коэффициент, равный 200,98 на пересечении со строкой «Y-пересечение».Метод Койка основан на использовании авторегрессионной модели: 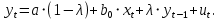 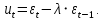 Запишем авторегрессионную модель с параметрами из столбца «Коэффициенты»: 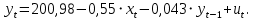 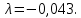 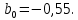 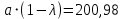 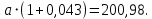 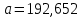 Для модели с распределенным лагом выберем величину лага l=3. Чтобы определить коэффициенты b1, b2, b3 исходной модели, под нижней подтаблицей Вывода итогов регрессии используем ссылки на необходимые ячейки и тождество: 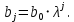 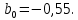 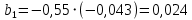 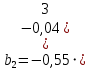 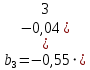 Запишем исходную модель с распределенным лагом, в которой оценки параметров получены методом Койка: 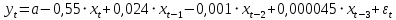 . .
Графически структура лага представлена на рис. 3. Для ее представления необходимо применить: Вставка – Диаграмма – Точечная – Точечная с гладкими кривыми и маркерами, к предварительно сформированным столбцам с номером лага и коэффициентом при лаговой переменной. 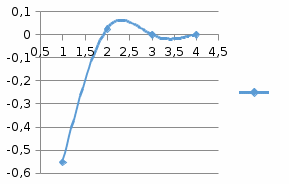 Рис. 3. Структура лага в модели Койка Чтобы определить средний и медианный лаг в модели Койка необходимо «вручную» использовать ссылки на необходимые ячейки согласно формулам: 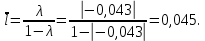 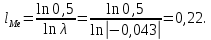
Вывод 1: Краткосрочный мультипликатор в модели Койка составил - - 0,55. Это означает, что увеличение доли кредиторской задолженности в заемном капитале в текущем месяце на 1 пункт приводит к увеличению чистой рентабельности активов в текущем месяце на 0,55 пункта, через месяц чистая рентабельность активов увеличивается на 0,02 пункта, через два месяца уменьшится на 0,001 пункта. Средний лаг показывает, что увеличение доли кредиторской задолженности в заемном капитале в среднем приведет к увеличению о чистой рентабельности активов через 0,045 месяца, т. е. менее чем через 1,35 дней. Медианный лаг показывает, что более половины влияния индекса потребительских цен на объем продаж происходит через 0,22 месяца (т. е. через 6,6 дней). Метод Алмон Для модели с распределенным лагом выберем величину лага l=3 и степень полинома k=3. Справа от столбца с переменной xt, начиная с пятой строки, сформируем переменные z0, z1, z2, z3, используя формулы: 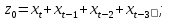 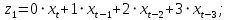 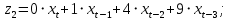 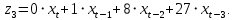 Чтобы оценить множественную линейную регрессию 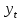 на переменные на переменные 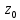 , , 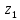 , , 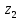 , , 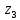 в MS Excel с помощью инструмента Регрессия надстройки Пакет анализа в главном меню программы MS Excel на вкладке Данные (в верхней строке) выберем опцию Анализ данных, а в списке Инструментов анализа выберем инструмент Регрессия. В качестве регрессанта в поле Входной интервал y выберем переменную в MS Excel с помощью инструмента Регрессия надстройки Пакет анализа в главном меню программы MS Excel на вкладке Данные (в верхней строке) выберем опцию Анализ данных, а в списке Инструментов анализа выберем инструмент Регрессия. В качестве регрессанта в поле Входной интервал y выберем переменную 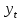 – чистая рентабельность активов, а в качестве регрессоров в поле Входной интервал Х укажем диапазон переменных – чистая рентабельность активов, а в качестве регрессоров в поле Входной интервал Х укажем диапазон переменных 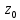 , , 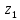 , , 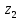 , , 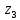 . Диапазон значений всех переменных начинаем выделять с пятой строки в MS Excel, не отмечаем «галочку» в опции Метки. . Диапазон значений всех переменных начинаем выделять с пятой строки в MS Excel, не отмечаем «галочку» в опции Метки. 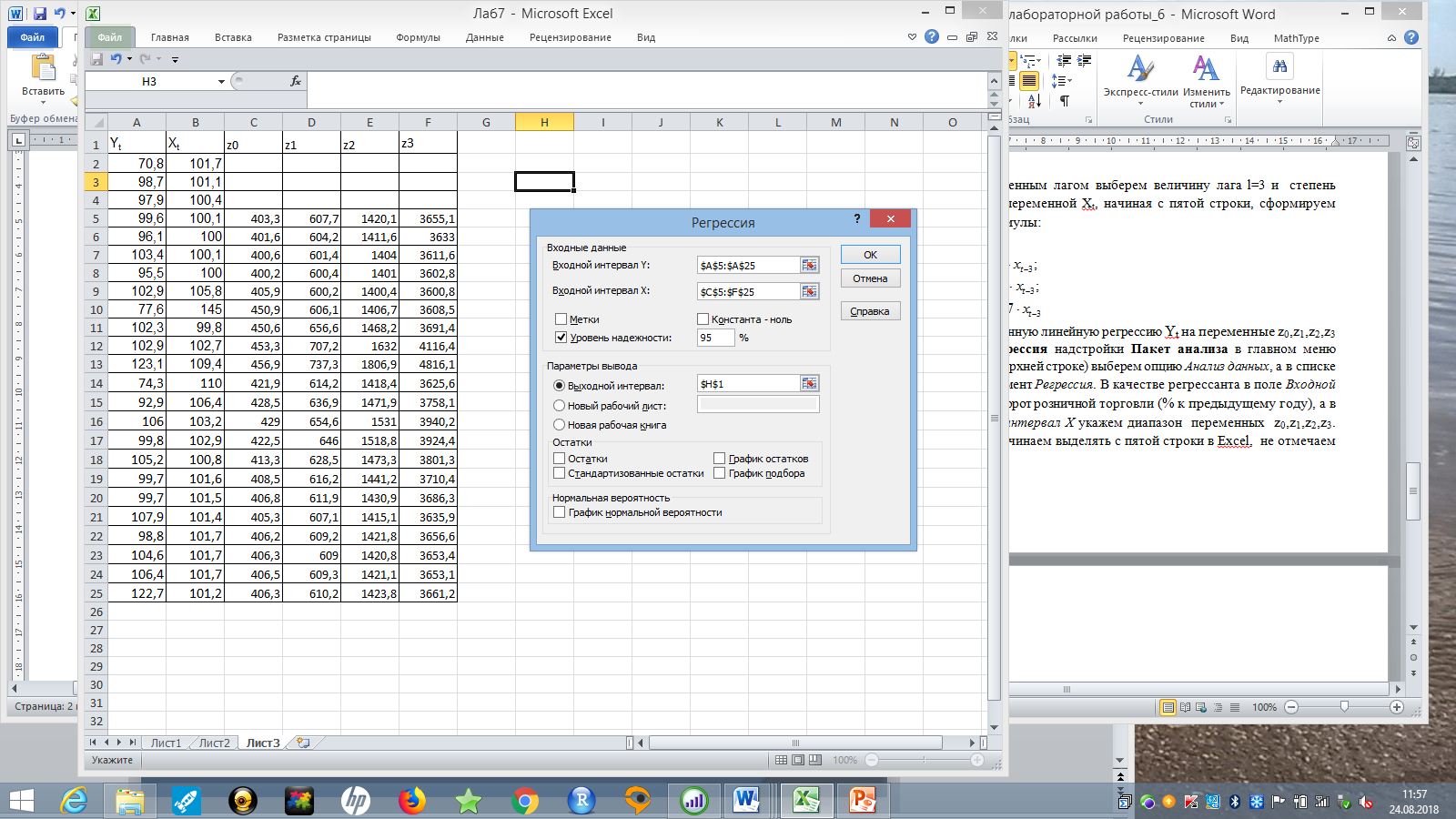 Рис. 4. Окно параметров регрессии с введенными значениями в MS Excel Далее, нажав на кнопку Ок, получаем результаты (рис. 5). 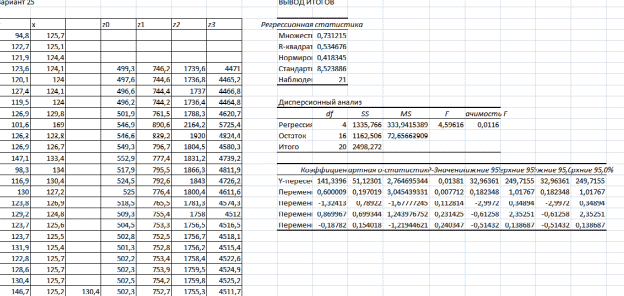 Рис. 5. Вывод результатов оценивания регрессии в MS Excel Запишем линейное уравнение множественной регрессии 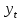 на на 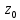 , , 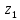 , ,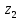 , , 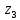 с параметрами из столбца «Коэффициенты» на рис. 5: с параметрами из столбца «Коэффициенты» на рис. 5: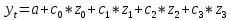 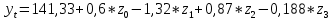 Чтобы определить коэффициенты b1, b2, b3 исходной модели, под нижней подтаблицей Вывода итогов регрессии используем ссылки на необходимые ячейки и тождества: 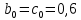 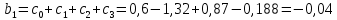 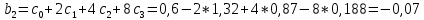 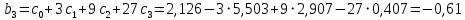
Запишем исходную модель с распределенным лагом, в которой оценки параметров получены методом Койка: 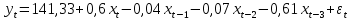 Графически структура лага представлена на рис. 6. Для ее представления необходимо применить: Вставка – Диаграмма – Точечная – Точечная с гладкими кривыми и маркерами, к предварительно сформированным столбцам с номером лага и коэффициентом при лаговой переменной. 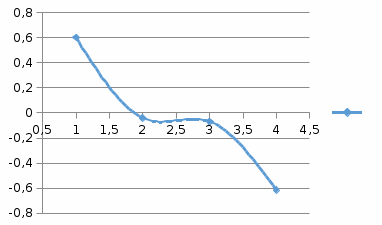 Рис. 3. Структура лага в модели Алмон Чтобы определить средний и медианный лаг в модели Алмон необходимо «вручную» использовать ссылки на необходимые ячейки согласно формулам: 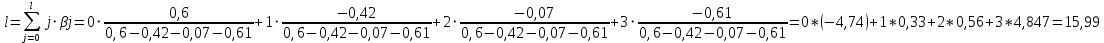
Вывод 2: Краткосрочный мультипликатор в модели Алмон составил 0,6. Это означает, что увеличение доли кредиторской задолженности в заемном капитале на 1 пункт в текущем месяце приводит к увеличению чистой рентабельности активов в текущем месяце на 0,6 пункта, через месяц чистая рентабельность активов снижается на 0,42 пункта, через два месяца – снижается на 0,07 процентных пункта, через три месяца – снижается на 0,61 процентных пункта. Средний лаг показывает, что доли кредиторской задолженности в заемном капитале в среднем приведет в увеличению чистой рентабельности активов через 16 месяцев, Медианный лаг в модели Алмон – это величина лага, для которого сумма относительных коэффициентов примерно равна 0,5. Поскольку β0= -4,74, что меньше, чем, 0,5, значит, в текущем месяце не будет реализована половина общего влияния доли кредиторской задолженности в заемном капитале на чистую рентабельность активов. |
