Динамическое программирование
 Скачать 0.94 Mb.
|
Ещё пример задания:Р-07. Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: 1. Прибавить 1 2. Умножить на 2 Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 29 и при этом траектория вычислений содержит число 14 и не содержит числа 25? Решение: у нас в задании две особые точки – числа 14 (через которое должна проходить траектория) и 25 (а сюда она попасть НЕ должна) сначала, так же, как и в задачах, рассмотренных ниже, составляем рекуррентную формулу, по которой будем вычислять количество  обозначить количество разных программ для получения числа N из начального числа:число N могло быть получено одной из двух операций: увеличением на 1 числа N-1; умножением на 2 числа N/2 (только для N, которые делятся на 2);  для нечётных чисел для чётных чиселдля начального числа 2 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды;  .составляем таблицу до первой особой точки – числа 14:
поскольку число 14 должно обязательно войти в траекторию, начинаем составлять вторую часть таблицы (до второй контрольной точки, 25) с этого числа заново, считая, что все ячейки для меньших чисел – нулевые
поскольку траектория не может проходить через 25, для N = 25 принимаем KN = 0 (в таблице эта ячейка выделена красным цветом) дальше заполняем оставшиеся ячейки второй части таблицы обычным способом (см. задачи ниже):
Ответ: 13. Решение (программа на Python, Б.С. Михлин): полная программа: # Функция подсчета количества цепочек команд (программ). # x - текущее число, t - цель (target). def nProg( x, t ): if x == t: # если цель достигнута, то return 1 # завершить функцию, посчитав цепочку (программу) if x==25 or x > t: # если x=25 или перелет, то return 0 # завершить функцию, не считая цепочку # x < t - продолжаем строить дерево: return nProg( x+1, t ) + nProg( x*2, t ) print( nProg( 2, 14 ) * nProg( 14, 29 ) ) Ответ: 13. Решение (2 таблицы, Python, А.Н. Носкин): идея: смотри разбор Р-09 a =[0]*15 # массив от 0 - 14 # заполняем от 2 до 14 a[2] = 1 for i in range(3,14+1): if i%2==0 and i>=4: a[i] = a[i-1] + a[i//2] else: a[i] = a[i-1] b =[0]*30 # массив от 0 - 29 # заполняем от 14 до 29 b[14] = 1 for i in range(15,29+1): if i==25: b[25] = 0 elif i%2==0 and i>=28: b[i] = b[i-1] + b[i//2] else: b[i] = b[i-1] print(a[14]*b[29]) # или так: print(a[-1]*b[-1]) Ответ: 13. Решение (динамическое программирование, Python, А.Н. Носкин): использование одной таблицы a =[0]*30 # массив от 0 - 29 # заполняем от 2 до 14 a[2] = 1 for i in range(3,14+1): if i % 2 == 0: a[i] = a[i-1] + a[i//2] else: a[i] = a[i-1] # заполняем с 15 до 29 for i in range(15,29+1): if i==25: a[25] = 0 elif i%2 == 0 and i>=28: a[i] = a[i-1] + a[i//2] else: a[i] = a[i-1] print( a[29] ) Ответ: 13. Решение (электронные таблицы Excel, LibreOffice Calc с помощью функции ИНДЕКС, А. Рогов): Основная идея решения заключается в том, что количество программ для данного числа равно сумме аналогичных значений чисел, в которые можно попасть из данного с помощью команд будем использовать возможность функции ИНДЕКС возвращать значение из ячейки, адрес которой можно вычислить. Для этого функции надо знать диапазон, в котором брать значения и номер строки и столбца внутри диапазона поскольку траектория содержит число 14, разобьем решение на два этапа найдем количество программ, для которых при исходном числе 2 результатом будет 14. В столбец А внесем числа от 2 до 14 так, чтобы каждое число совпадало с номером строки 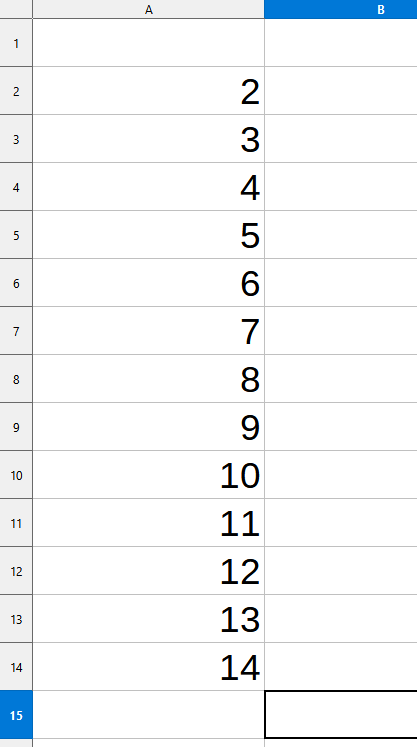 в столбец B внесем формулу для подсчета количества программ. В ячейке B2 это будет формула =ИНДЕКС(B$1:B$100;A2+1)+ИНДЕКС(B$1:B$100;A2*2) здесь B$1:B$100 – это диапазон, внутри которого мы будем брать значения. Начинаться он должен с первой строки для того, чтобы нумерация строк внутри диапазона совпала с нумерацией чисел при вычислениях. А заканчиваться в такой ячейке, номер которой позволит взять любое число. В данном случае для расчета количества программ для числа 13 надо взять значения чисел 14 и 26. Значит, диапазон должен включать хотя бы 26 строк. Число 100 взято с запасом. Абсолютная адресация позволит эту формулу скопировать в другие ячейки столбца B. A2+1 – это вычисление из какой строки надо взять данные. По условию задачи у нас две команды: +1 и *2, соответственно, для подсчета количества программ в ячейке B2, которая соответствует числу 2, мы возьмем числа из строк 2 + 1 = 3 и 2 * 2 = 4 данную формулу мы копируем на ячейки диапазона B3:B13, а в ячейку B14 внесем 1 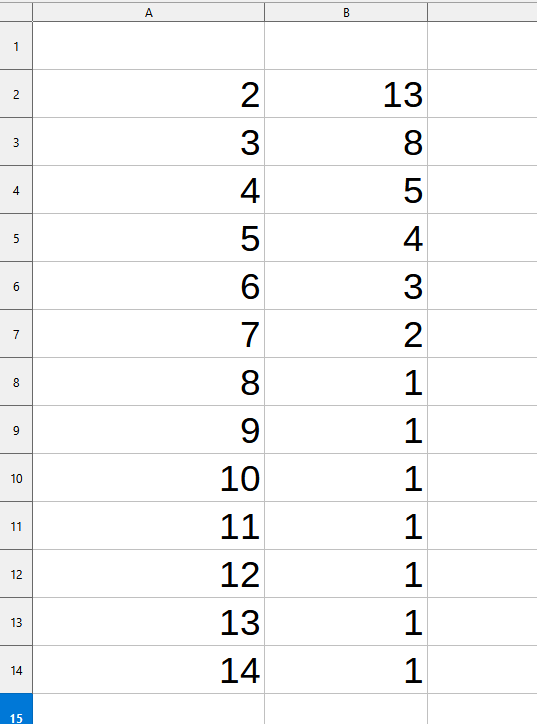 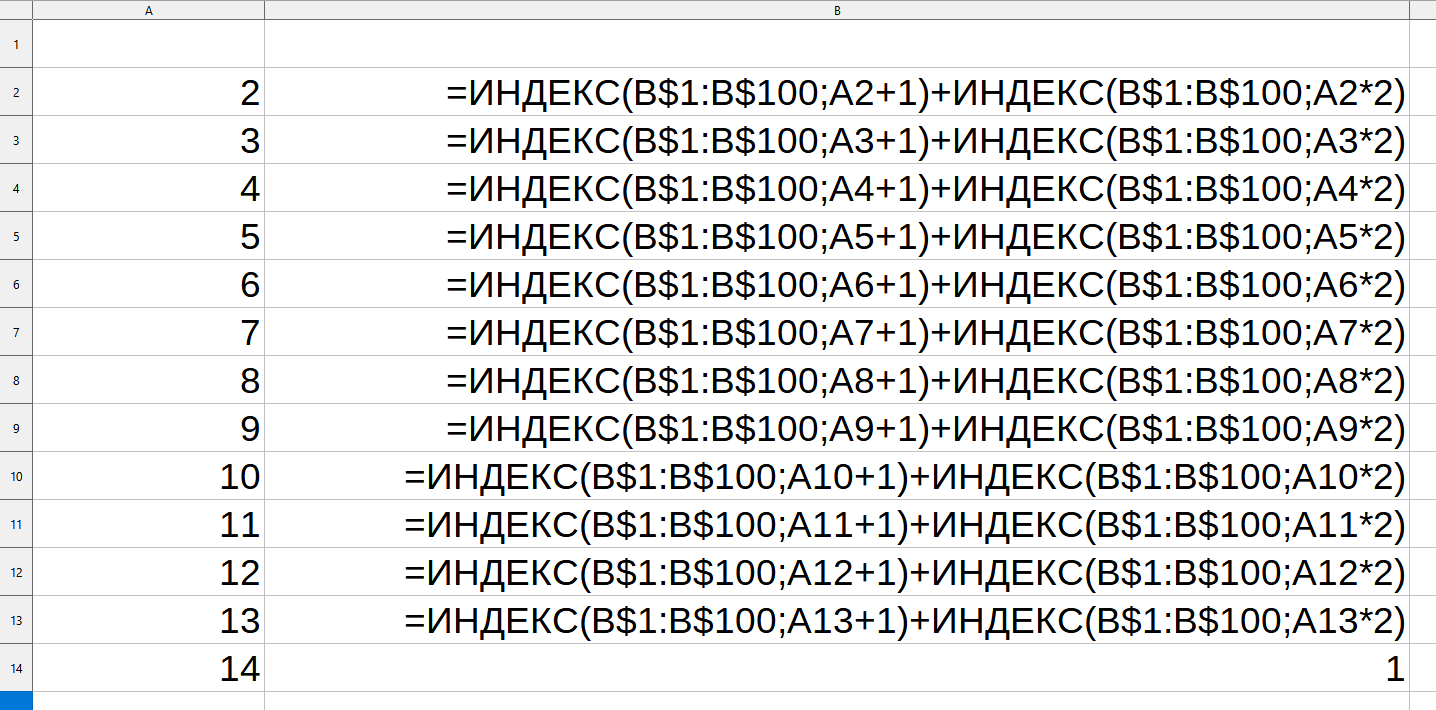 вторая часть решения - количество программ из 14 в 29. Построим данную часть правее, в столбцах С и D. Для корректной работы функции ИНДЕКС с формулами важно числа писать в совпадающие по номеру строки, а диапазон в формуле начинать с первой строки. Внесем формулу =ИНДЕКС(D$1:D100;C14+1)+ИНДЕКС(D$1:D100;C14*2) в ячейку D14, скопируем ее до ячейки D28, а в ячейку D29 внесем 1. Для того, чтобы учесть, что в 25 нельзя, просто удалим значение в столбце D напротив 25 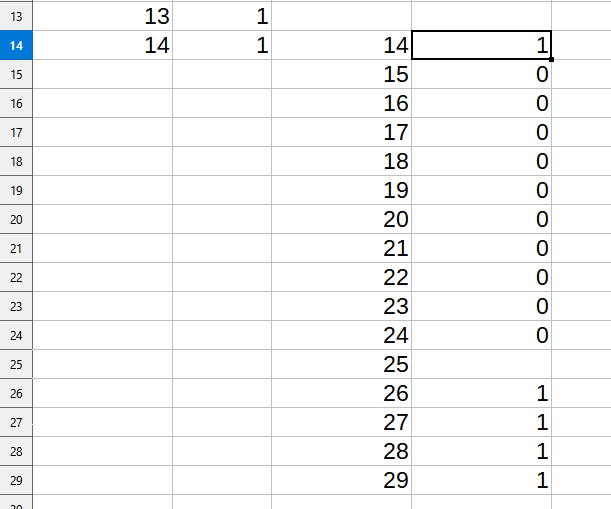 в ячейке B2 получилось количество программ, которыми можно попасть из 2 в 14, а в ячейке D14 количество программ из 14 в 29 минуя 25. Для получения итогового ответа перемножим эти числа: 13*1=13 Ответ: 13 Подробнее о методе решения: https://youtu.be/bHUpKN8iftA |