Динамическое программирование

• Название: Динамическое программирование
• Дата: 18.12.2021
• Размер: 0.7 Mb.
• Имя файла: ege23.doc
• Тип: Решение; #307871
• страница: 2 из 11

Ещё пример задания:

Р-08 (демо-вариант 2018 г.). Исполнитель М17 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1

2. Прибавить 2

3. Умножить на 3

Первая команда увеличивает число на экране на 1, вторая – увеличивает его на 2, а третья – умножает его на 3. Программа для исполнителя М17 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 12 и при этом траектория вычислений содержит числа 8 и 10?

Решение:

1. 
   запишем рекуррентную формулу для вычисления – количества возможных программ для получения числа N из некоторого начального числа:
   

, если N не делится на 3

, если N делится на 3

2. 
   все допустимые программы можно разбить на 3 части:
   

– переход от 2 до 8

– переход от 8 до 10

– переход от 10 до 12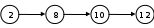

3. 
   обозначим через количеств возможных программ получения числа b из числа a
   
4. 
   очевидно, что если траектория проходит через c, то для любого c, такого что a < c < b
   
5. 
   поэтому
   
6. 
   вычисляем эти значения отдельно стандартным способом по рекуррентным формулам п. 1:
   

N	2	3	4	5	6	7	8
KN	1	1	2	3	6	9	15

N	8	9	10		10	11	12
KN	1	1	2		1	1	2

7. 
   и перемножаем: 15  2  2 = 60
   
8. 
   Ответ: 60.
   

Решение (программа на Python, Б.С. Михлин):

1. 
   полная программа:
   

# Функция подсчета количества цепочек команд (программ).

# x - текущее число, t - цель (target).

def nProg( x, t ):

if x == t: # если цель достигнута, то

return 1 # завершить функцию, посчитав цепочку (программу)

if x > t: # если перелет, то

return 0 # завершить функцию, не считая цепочку

# x < t - продолжаем строить дерево:

return nProg( x+1, t ) + nProg( x+2, t ) + nProg( x*3, t )

print( nProg( 2, 8 ) * nProg( 8, 10 ) * nProg( 10, 12 ) )

2. 
   Ответ: 60.