Динамическое программирование

• Название: Динамическое программирование
• Дата: 18.12.2021
• Размер: 0.7 Mb.
• Имя файла: ege23.doc
• Тип: Решение; #307871
• страница: 1 из 11

© К. Поляков, 2009-2021

23 (повышенный уровень, время – 8 мин)

Тема: динамическое программирование.

Что проверяется:

Умение анализировать результат исполнения алгоритма

1.6.2. Вычислимость. Эквивалентность алгоритмических моделей (?).

1.1.3. Умение строить информационные модели объектов, систем и процессов

в виде алгоритмов (?).

Что нужно знать:

• 
  динамическое программирование – это способ решения сложных задач путем сведения их к более простым задачам того же типа
  
• 
  с помощью динамического программирования решаются задачи, которые требуют полного перебор вариантов:
  
  • 
    «подсчитайте количество вариантов…»
    
  • 
    «как оптимально распределить…»
    
  • 
    «найдите оптимальный маршрут…»
    
• 
  динамическое программирование позволяет ускорить выполнение программы за счет использования дополнительной памяти; полный перебор не требуется, поскольку запоминаются решения всех задач с меньшими значениями параметров
  

Пример задания:

Р-09 (демо- 2021). Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 20, и при этом траектория вычислений содержит

число 10?

Решение (теоретическое):

1. 
   запишем рекуррентную формулу для вычисления – количества возможных программ для получения числа N из некоторого начального числа:
   

, если N не делится на 2

, если N делится на 2

2. 
   все допустимые программы можно разбить на 2 части:
   

– переход от 1 до 10

– переход от 10 до 20

3. 
   обозначим через количеств возможных программ получения числа b из числа a
   
4. 
   очевидно, что если траектория проходит через c, то для любого c, такого что a < c < b
   
5. 
   поэтому
   
6. 
   вычисляем эти значения отдельно стандартным способом по рекуррентным формулам п. 1:
   

N	1	2	3	4	5	6	7	8	9	10
KN	1	2	2	4	4	6	6	10	10	14

N	10	11	12	13	14	15	16	17	18	19	20
KN	1	1	1	1	1	1	1	1	1	1	2

7. 
   (И.В. Степанов) этот результат достаточно очевиден и без таблицы: понятно, что получить 20 из 10 с помощью заданных команд можно только двумя способами – добавляя по единице или умножив 10 на 2
   
8. 
   перемножаем результаты двух этапов: 14  2 = 28
   
9. 
   Ответ: 28.
   

Решение (электронные таблицы Excel, LibreOffice Calc):

1. 
   главная проблема при решении этого задания – высокая вероятность арифметической ошибки, поэтому во время компьютерного экзамена можно реализовать этот же алгоритм в электронных таблицах
   
2. 
   сначала найдём количество программ для перехода от числа 1 к числу 10; построим ряд этих чисел в первой строке и запишем начальную единицу в первую ячейку второй строки:
   

3. 
   в строке 2 будем считать значение K_N по разным формулам для чётных и нечётных N; предположим, что значение 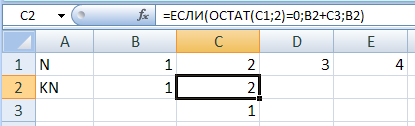записано в строке 3 того же столбца; тогда в ячейку C2 нужно записать такую формулу:
   

4. 
   следующий вопрос – как получить ; для этого нужно:
   

а) вычислить значение N/2:

C1/2

б) найти это значение в диапазоне B1:K1:

ПОИСКПОЗ(C1/2;$B$1:$K$1;0)

функция ПОИСКПОЗ возвращает номер элемента в массиве; в данном случае она ищет значение C1/2 в массиве B1:K1; последний аргумент 0 означает, что ищем точное совпадение

в) взять значение в строке 2 того же столбца, это и будет :

=СМЕЩ($A$2;0;ПОИСКПОЗ(C1/2;$B$1:$K$1;0))

функция СМЕЩ находит значение ячейки, которая смещена относительно ячейки A2; второй аргумент задаёт смещение по строкам (0 – в той же строке), а третий – смещение по столбцам, такое, какое вернула функция ПОИСКПОЗ

5. 
   вот как выглядит формула в ячейке C3: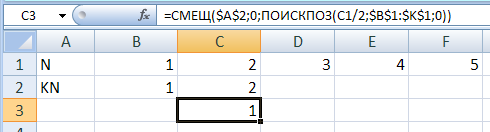
   

6. 
   теперь копируем («протягиваем») формулы в C2 и С3 вправо до конца таблицы:
   

7. 
   здесь #Н/Д означает, что значение N/2 не найдено в первой строке (оно получилось дробное), но по формуле, которую мы записали во C2 и скопировали на всю вторую строку, для нечётных N это значение не используется
   
8. 
   вторую часть таблицы можно построить так же, но можно просто учесть, что второе слагаемое в формуле будет только для N = 20:
   

9. 
   перемножая значения последних ячеек двух таблиц, получаем 14  2 = 28.
   
10. 
    Ответ: 28.
    
11. 
    Про работу функций СМЕЩ и ПОИСКПОЗ можно посмотреть здесь: https://www.youtube.com/watch?v=BQN2nxLOaLg
    

Решение (электронные таблицы OpenOffice Calc):

1. 
   в электронных таблицах OpenOffice Calc нужно использовать английские названия функций:
   

C2: =IF(MOD(C1;2)=0;B2+C3;B2)

C3: =OFFSET($A$2;0;MATCH(C1/2;$B$1:$K$1;0))

2. 
   Ответ: 28.
   

Решение (рекурсивная программа, Python):

3. 
   для проверки (если есть время) можно написать программу, реализующую тот же алгоритм
   
4. 
   вычисления по рекуррентным формулам можно организовать с помощью рекурсии
   
5. 
   рекурсивная функция, которая возвращает количество программ для преобразования числа start в число x, может быть написана так:
   

def numProg( start, x ):

if x < start: return 0 # (1)

if x == start: return 1 # (2)

K = numProg( start, x-1 ) # (3)

if x % 2 == 0:

K += numProg( start, x//2 ) # (4)

return K

6. 
   если число x меньше, чем начальное значение, количество программ равно 0 (строка (1))
   
7. 
   если число x равно начальному значению, количество программ равно 1 (строка (2))
   
8. 
   в остальных случаях всегда учитываем количество программ предыдущего числа (если последняя команда программы будет +1), см. строку (3)
   
9. 
   если число чётное, нужно добавить ещё и количество программ для числа x//2 (строка (4))
   
10. 
    в основной программе вычисляем количество программ от 1 до 10 и умножаем на количество программ от 10 до 20:
    

print( numProg(1,10)*numProg(10,20) )

11. 
    Ответ: 28.
    
12. 
    аналогичная программа на Паскале:
    

function numProg( start, x: integer ): integer;

var K: integer;

begin

if x < start then numProg := 0

else if x = start then numProg := 1

else begin

K := numProg( start, x-1 );

if x mod 2 = 0 then

K := K + numProg( start, x div 2 );

numProg := K;

end;

end;
begin

writeln( numProg(1,10)*numProg(10,20) );

end.

13. 
    аналогичная программа на C++:
    

#include

using namespace std;
int numProg( int start, int x ) {

int K;

if( x < start ) return 0;

if( x == start ) return 1;

K = numProg( start, x-1 );

if( x % 2 == 0 )

K += numProg( start, x / 2 );

return K;

}
int main()

{

cout << numProg(1,10)*numProg(10,20);

}

Решение (программа на Python, А. Сидоров):

1. 
   можно использовать другую идею: начав со значения start, мы можем попасть в x либо через значение start+1, либо через 2*start
   
2. 
   получается такой краткий вариант программы:
   

def numProg( start, x ):

if x < start: return 0

if x == start: return 1

return numProg(start+1,x) + numProg(start*2,x)
print( numProg(1,10)*numProg(10,20) )

Главное его достоинство в том, что не нужно делать проверку на чётность x и использовать обратные операции.

3. 
   Ответ: 28.
   
4. 
   аналогичная программа на Паскале:
   

function numProg( start, x: integer ): integer;

var K: integer;

begin

if x < start then numProg := 0

else if x = start then numProg := 1

else

numProg := numProg(start+1,x) + numProg(start*2,x);

end;
begin

writeln( numProg(1,10)*numProg(10,20) );

end.

5. 
   аналогичная программа на C++:
   

#include

using namespace std;
int numProg( int start, int x ) {

int K;

if( x < start ) return 0;

if( x == start ) return 1;

return numProg(start+1,x) + numProg(start*2,x);

}
int main()

{

cout << numProg(1,10)*numProg(10,20);

}

6. 
   (К. Поляков) Программу из п. 2 можно легко обобщить на случай, когда траектория не должна содержать некоторые числа. Для этого в функцию нужно добавить третий параметр – список запрещённых значений blocked. Если начальное значение есть в списке blocked, функция возвращает 0:
   

def numProg( start, x, blocked ):

if x < start: return 0

if start in blocked: return 0

if x == start: return 1

return numProg(start+1,x,blocked) + numProg(start*2,x,blocked)

7. 
   Модифицированная программа находит количество программ, для которых траектория не содержит числа 15:
   

print( numProg(1,10,[])*numProg(10,20,[15]) )
Решение (динамическое программирование, Python):

1. 
   рекурсивная программа может работать очень медленно для больших чисел или при большем количестве команд; вместо этого можно применить динамическое программирование, заполняя массив по тем же формулам
   
2. 
   создаём массив
   

TARGET = 20

K = [0]*(TARGET+1)

константа TARGET означает наибольшее число, которое нужно получить; размер массива на единицу больше, элемент K[0] мы использовать не будем, так удобнее (ведь нас интересуют числа, начиная с 1)

3. 
   записываем в первый элемент единицу:
   

K[1] = 1

4. 
   вот процедура, которая заполняет по приведённым выше формула элементы массив с индексами от start+1 до x (элемент K[start] должен быть уже заполнен!)
   

def fillArray( start, x ):

for i in range(start+1,x+1):

K[i] = K[i-1]

if i % 2 == 0 and i // 2 >= start:

K[i] += K[i//2]

в условие добавилась вторая часть (i//2 >= start) для того, чтобы не захватывать значения K[i] при i<start

5. 
   основная программа заполняет две части массива и выводит результат:
   

fillArray( 1, 10 )

fillArray( 10, 20 )

print( K[TARGET] )

6. 
   обратите внимание, что после первого вызова процедуры fillArray значение K[10] уже определено, так что всё готово для заполнения второй части
   
7. 
   Ответ: 28.
   
8. 
   аналогичная программа на Паскале:
   

const TARGET = 20;

var K: array[1..TARGET] of integer;
procedure fillArray( start, x: integer );

var i: integer;

begin

for i:=start+1 to x do begin

K[i] := K[i-1];

if (i mod 2 = 0) and (i div 2 >= start) then

K[i] := K[i] + K[i div 2];

end;

end;
begin

K[1] := 1;

fillArray( 1, 10 );

fillArray( 10, 20 );

writeln( K[TARGET] );

end.

9. 
   аналогичная программа на C++:
   

#include

using namespace std;
const int TARGET = 20;

int K[TARGET+1] = {0, 1};

void fillArray( int start, int x ) {

for( int i = start+1; i<=x; i++ ) {

K[i] = K[i-1];

if( i % 2 == 0 and i / 2 >= start )

K[i] += K[i/2];

}

}
int main() {

fillArray( 1, 10 );

fillArray( 10, 20 );

cout << K[TARGET] << endl;

}

Решение (динамическое программирование, 2 таблицы, А.Н. Носкин):

1. 
   идея решения задачи в том, чтобы получить количество решений из числа "1" в число "10" (число, через которое проходят все траектории), а потом получить количество решений из числа "10" в число "20", при этом во втором случае расчеты начинаются сначала, то есть количество решений при числе "10" равно 1;
   
2. 
   результатом решения задачи будет перемножения количества решений одной таблицы на количество решений второй таблицы;
   
3. 
   создаём массив и заполняем количеством решений для каждого числа; при этом следует учесть формулы для пересчёта количества решений:
   

a[i] = a[i-1] - для чисел не кратных 2;

a[i] = a[i-1] + a[i//2] - для чисел кратных 2

4. 
   фрагмент кода для вычисления количества решений до числа "10".
   

a =[0]*11 # массив от 0 - 10

# табличка от 1 до 10

a[1] = 1

for i in range(2,10+1):

if i%2==0 and i>=2:

a[i] = a[i-1] + a[i//2]

else: a[i] = a[i-1]

5. 
   Фрагмент кода для вычисления количества решений от числа "10" до числа "20". При этом важно учесть, что команда Умножить на 2 работает с индекса 20 и более, так как 10*2 = 20.
   

b =[0]*21 # массив от 0 - 20

# табличка от 10 до 20

b[10] = 1

for i in range(11,20+1):

if i%2==0 and i>=20:

b[i] = b[i-1] + b[i//2]

else: b[i] = b[i-1]

6. 
   Результат решения задачи будет перемножение последних элементов массива.
   

print(a[10]*b[20])

Вывод результата можно организовать и так:

print(a[-1]*b[-1])

7. 
   Ответ: 28.