НОШКМмм. ккр 1. Задача универсального алгоритма Какие подходы к уточнению понятия алгоритма существуют
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Зачем в математике потребовалось формализовать понятие алгоритма? В чем состоит задача универсального алгоритма? Какие подходы к уточнению понятия алгоритма существуют? Какова формулировка тезиса Черча? Что он означает? Темы для рефератов: Основатели теории алгоритмов — Клини, Черч, Пост, Тьюринг (выбрать одного). 5. Машина Поста Машина Поста – это абстрактная (несуществующая реально) вычислительная машина, созданная для уточнения (формализации) понятия алгоритма. Представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы. В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой. Если задача имеет алгоритмическое решение, то она представима в форме команд для машины Поста. Машина Поста состоит из … бесконечной ленты, поделенной на одинаковые ячейки (секции). Ячейка может быть пустой (0 или пустота) или содержать метку (1 или любой другой знак), головки (каретки), способной передвигаться по ленте на одну ячейку в ту или иную сторону, а также способной проверять наличие метки, стирать и записывать метку. Текущее состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты – информация о том, какие секции пусты, а какие отмечены. Шаг – это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы. Кареткой управляет программа, состоящая из строк команд. Каждая команда имеет следующий синтаксис: i K j, где i - номер команды, K – действие каретки, j - номер следующей команды (отсылка). Всего для машины Поста существует шесть типов команд: V j - поставить метку, перейти к j-й строке программы. X j - стереть метку, перейти к j-й строке программы. <- j - сдвинуться влево, перейти к j-й строке программы. -> j - сдвинуться вправо, перейти к j-й строке программы. ? j1; j2 - если в ячейке нет метки, то перейти к j1-й строке программы, иначе перейти к j2-й строке программы. ! – конец программы (стоп)  У команды «стоп» отсылки нет. Варианты окончания выполнения программы на машине Поста: Команда "стоп" - корректная остановка. Возникает в результате выполнения правильно написанного алгоритма. Выполнение недопустимой команды – нерезультативная остановка. Случаи, когда головка должна записать метку там, где она уже есть, или стереть метку там, где ее нет, являются аварийными (недопустимыми). Уход в бесконечность, зацикливание. Машина Поста в результате работы алгоритма может вообще не остановиться (никогда не дойти до команды «стоп» и никогда не завершиться аварийной ситуацией). Элементарные действия (команды) машина Поста проще команд машины Тьюринга. Поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга. Почему достаточно лишь два различных символа (есть метка, нет метки)? Дело в том, что любой алфавит может быть закодирован двумя знаками; в зависимости от алфавита возрастать может только количество двоичных символов в букве алфавита. 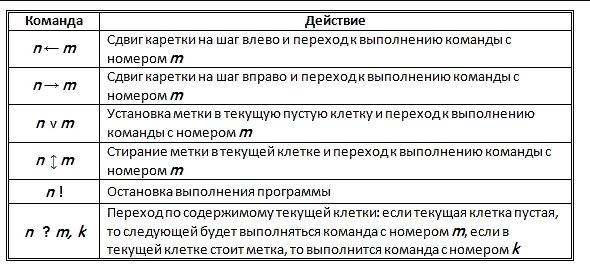 6. Машина Тьюринга В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга. Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи. Что собой представляет машина Тьюринга? Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой. Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице. Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие: Внешний алфавит. Конечное множество (например, А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ. Внутренний алфавит. Конечное множество состояний головки (автомата). Одно из состояний (например, q1) должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние останова. Таблица переходов. Описание поведения автомата (головки) в зависимости от состояния и считанного символа. Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия: Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой). Передвигаться на одну ячейку влево или вправо. Менять свое внутреннее состояние. Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния). 7. Предложенный А.А.Марковым способ уточнения понятия алгоритма основан на понятии нормального алгоритма, который определяется следующим образом. Пусть задан алфавит А и система подстановок В. Для произвольного слова Р подстановки из В подбираются в том же порядке, в каком они следуют в В. .Если подходящей подстановки нет, то процесс останавливается. В противном случае берется первая из подходящих подстановок и производится замена ее правой частью первого вхождения ее левой части в Р. Затем все действия повторяются для получившегося слова P1. Если применяется последняя подстановка из системы В, процесс останавливается. Такой набор предписаний вместе с алфавитом А и набором подстановок В определяют нормальный алгоритм. Процесс останавливается только в двух случаях: 1) когда подходящая подстановка не найдена; 2) когда применена последняя подстановка из их набора. Различные нормальные алгоритмы отличаются друг от друга алфавитами и системами подстановок. Приведем пример нормального алгоритма, описывающего сложение -натуральных чисел (представленных наборами единиц). Пример Алфавит: Система подстановок В: А = (+, 1) 1 + → + 1 + 1 → 1 1 → 1 Слово Р: 11+11+111 Последовательная переработка слова Р с помощью нормального алгоритма Маркова проходит через следующие этапы: Р = 11 + 11 + 111 Р5 = + 1 + 111111 Р1 = 1 + 111 + 111 Р6 = ++ 1111111 Р2 = + 1111 + 111 Р7 = + 1111111 Р3 = + 111 + 1111 Р8 = 1111111 Р4 = + 11 + 11111 Р9 = 1111111 Нормальный алгоритм Маркова можно рассматривать как универсальную форму задания любого алгоритма. Универсальность нормальных алгоритмов декларируется принципом нормализации: для любого алгоритма в произвольном конечном алфавите А можно построить эквивалентный ему нормальный алгоритм над алфавитом А, 7.1 Краткие теоретические сведения Нормальные алгоритмы Маркова (далее — НАМ), введенные советским математиком А. А. Марковым, представляют собой класс алгоритмов, применимых к словам некоторого алфавита. Каждый НАМ определяется указанием алфавита, в котором он действует, и схемы НАМ. Алфавитом НАМ может служить любой конечный алфавит A. Формулой подстановки в алфавите A называется выражение типа p → q (простая подстановка, в эмуляторе обозначена как ->) или p ↦ q (заключительная подстановка, в эмуляторе обозначена как =>), где p и q — некоторые слова в алфавите A, называемые, соответственно, левой и правой частями формулы подстановки. Каждый НАМ в алфавите A имеет конечное число формул подстановки. Их записывают в виде списка, который называется схемой алгоритма. Применение НАМ к некоторому слову S заключается в следующем. В списке формул подстановки ищется первая из тех формул, в которой левая часть входит в S. Находится 1-е вхождение левой части формулы в S и вместо этого вхождения подставляется правая часть формулы. Получается новое слово S'. Cо словом S' производятся те же действия и т.д. Данный процесс обрывается в 2-х случаях: к очередному слову применена одна из заключительных формул подстановки; в слово не входит ни одна из левых частей формул подстановки. Получаемое последнее слово является результатом применения НАМ к исходному слову S. 8. Рекурсия — это способ определения множества объектов через само это множество на основе заданных простых базовых случаев. Рекурсивная процедура (функция) — это процедура (функция), которая вызывает сама себя напрямую или через другие процедуры и функции. Рекурсия — это широко распространённый метод, понятный и без математической формализации, интуитивно близкий любому «человеку с улицы». Рекурсия кроется в идее „картины в картине" Приложение Рекурсивные картины, она же обнаруживается в стихах Рингельнаца «...а этот глист страдал глистами, что мучились глистами сами» (перевод Л. Макаровой).   Функция называется рекурсивной, если в своем теле она содержит обращение к самой себе с измененным набором параметров. При этом количество обращений конечно, так как в итоге решение сводится к базовому случаю, когда ответ очевиден. В рекурсивных функциях несколько раз используется return. В базовом случае возвращается конкретный результат (в примере – значение а ), а общий случай предусматривает вызов функцией себя же, но с меняющимися значениями отдельных параметров (в примере изменяется только номер члена последовательности, при этом не меняются разность и первый член прогрессии). В программировании выделяют прямую и косвенную рекурсию. Прямая рекурсия предусматривает непосредственное обращение рекурсивной функции к себе, но с иным набором входных данных. Косвенная (взаимная) рекурсия представляет собой последовательность взаимных вызовов нескольких функций, организованная в виде циклического замыкания на тело первоначальной функции, но с иным набором параметров. Для решения задач рекурсивными методами разрабатывают следующие этапы, образующие рекурсивную триаду: параметризация – выделяют параметры, которые используются для описания условия задачи, а затем в решении; база рекурсии – определяют тривиальный случай, при котором решение очевидно, то есть не требуется обращение функции к себе; декомпозиция – выражают общий случай через более простые подзадачи с измененными параметрами. РЕФЕРАТ Чёрч Алоизо. Чёрч Алоизо (Church Alonzo) (родился 14.6.1903, Вашингтон) – крупный американский логик и математик, профессор математики Принстонского и Калифорнийского универститетов. С 1936 года редактор журнала «TheJournalofSymbolicLogic». Занимался исследованиями проблемы логической семантики. Внес большой вклад в развитие математической логики и теории автоматов. Он знаменит тем, что в 1935 году построил первый пример неразрешимой массовой проблемы, которая состоит в требовании найти алгоритм для решения некоторой серии «единичных» проблем. Массовая проблема неразрешима, если ее решения, то есть требуемого алгоритма, е существует. Им же дано доказательство неразрешимости проблемы для узкого исчисления предикатов, то есть доказательство того, что не существует алгоритма, который по виду формулы этого исчисления определял бы, выражает эта формула общелогическую истину или нет. Алоизо Чёрч автор книги «Введение в математическую логику» (1956), в которой разъяснил свое понимание метода математической логики, определил ее первичные понятия и изложил исчисление высказываний или пропорциональное исчисление, функциональные исчисления первого порядка, чистое функциональное исчисление первого порядка и функциональные исчисления второго порядка. А.Чёрч дает определения таких категорий, как имя, константы и переменные функции, символы, связки, операторы, кванторы, проблема разрешения, непротиворечивость и полнота системы аксиом. Математическую логику А.Чёрч называет формальной логикой, предмет которой изучается методом построения формализованных языков. «Обычно (формальная) логика, - пишет он, - занимается анализом предложений и доказательств; при этом основное внимание обращается на форму в отвлечении от содержания…»[1] Поскольку естественные языки на протяжении длительных исторических периодов развивались под влиянием практических потребностей легкости общения, постольку они не отличаются точностью и надежностью, что приводит к ошибкам в рассуждениях. Чтобы избежать возможных ошибок, А.Черч предлагает употреблять для логических целей специально созданный язык – формализованный язык, в который из обычных языков будут перенесены собственные имена. При этом он подчеркивает, что в хорошо построенном языке каждое имя должно иметь точно один смысл, если ставится задача обеспечить однозначность в формализованных языках. Суждение А.Чёрч определяет так: «Всякий концепт истинного значения называется суждением независимо от того, является ли он смыслом какого-либо предложения».[2] В математической логике большую роль играет тезис Чёрча, принцип, согласно которому класс функций, вычислимых с помощью алгоритмов в широком интуитивном смысле, совпадает с классом частично рекурсивных функций. Тезис Чёрча – это естественнонаучный факт, подтверждаемый опытом, накопленным в математике за всю ее историю. Все известные в математике примеры алгоритмов удовлетворяют ему. Различным уточнениям интуитивного понятия алгоритма соответствуют свои формулировки тезиса Чёрча. Тезис Тьюринга заключается в том, что всякая вычислимая в интуитивном смысле функция вычислима с помощью машины Тьюринга, а принцип нормализации Маркова – в том, что всякая вычислимая в интуитивном смысле функция вычислима с помощью некоторого нормального алгоритма. Из эквивалентности известных уточнений понятия алгоритма следует эквивалентность соответствующих вариантов тезиса Чёрча. Этот факт является еще одним подтверждением тезиса Чёрча. Тезис Чёрча не может быть строго доказан, так как в его формулировке участвует неточное понятие «алгоритм в интуитивном смысле». Были попытки опровергнуть тезис Чёрча, однако они к успеху не привели. Принятие тезиса Чёрча полезно в теории алгоритмов и ее приложениях. Во-первых, при доказательстве существования тех или иных конкретных алгоритмов – машин Тьюринга, рекурсивных функций, нормальных алгоритмов – можно, опираясь на тезис Чёрча, ограничиваться интуитивно ясными построениями и не выписывать соответствующие формальные схемы. Кроме того, тезис Чёрча является основанием для вывода о неразрешимости данной алгоритмической проблемы после того, как строго доказано, что эта проблема не может быть решена в рамках того или иного уточнения понятия алгоритма. |
