Лабораторная работа асд. Лабораторные работы_по_АСД. Дисциплина Алгоритмы и структуры данных Отчёт по лабораторной работе

• Название: Дисциплина Алгоритмы и структуры данных Отчёт по лабораторной работе
• Анкор: Лабораторная работа асд
• Дата: 27.06.2022
• Размер: 3.09 Mb.
• Имя файла: Лабораторные работы_по_АСД.docx
• Тип: Лабораторная работа; #616986
• страница: 8 из 9

Задача 7. Написать рекурсивную программу вычисления n-го числа Фибоначчи. Последовательность чисел Фибоначчи имеет вид: 1, 1, 2, 3, 5, 8, 13, 21, 34, … (a_n=a_n-1+ a_n-2), для n начиная с 3.

Все используемые идентификаторы представлены в таблице 38

Таблица 38 – Идентификаторы

Имя переменной			Тип переменной		Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
n	n	integer		Номер числа Фибоначчи
Промежуточные данные
c	c	integer		Номер текущего числа Фибоначчи
Результирующие данные
f	f	integer		Найденное число Фибоначчи

Блок схема алгоритма решения задачи представлена на рисунке 75.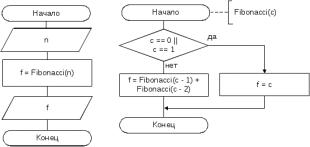



Рисунок 74. Блок схема алгоритма решения задачи 7
Программа на C#:

using System;
namespace lr7_z7

{

class Program

{

static void Main(string[] args)

{

int Fibonacci(int c)

{

if (c == 0 || c == 1)

return c;

else

return Fibonacci(c - 1) + Fibonacci(c - 2);

}
Console.Write("Введите n: ");

int n = int.Parse(Console.ReadLine());

int f = Fibonacci(n);

Console.Write("a[{0}] = {1}", n, f);

Console.ReadKey();

}

}

} }

Скриншот результата работы программы представлен на рисунке 76.



Рисунок 75. Скриншот результата работы программы задачи 7.
Задача 8. Написать рекурсивную программу поиска минимального элемента массива.

Все используемые идентификаторы представлены в таблице 39

Таблица 39 – Идентификаторы

Имя переменной			Тип переменной		Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
N	N	integer		Количество элементов в массиве
mas	mas	integer[]		Исходный массив
Промежуточные данные
i	i	integer		Переменная цикла
min	min	integer		Текущий минимальный элемент
a	a	integer[]		Исходный массив
Результирующие данные
m	m	integer		Минимальный элемент

Блок схема алгоритма решения задачи представлена на рисунке 77.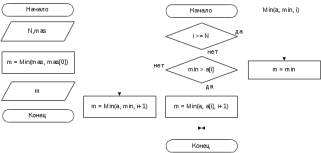



Рисунок 76. Блок схема алгоритма решения задачи 8
Программа на C#:

using System;
namespace lr7_z8

{

class Program

{

static void Main(string[] args)

{

Console.Write("Введите n: ");

int N = Convert.ToInt32(Console.ReadLine());

Console.WriteLine("Введите массив: ");

int[] mas = new int[N];

for (int i = 0; i < N; i++)

mas[i] = Convert.ToInt32(Console.ReadLine());

int m = Min(mas, mas[0]);

Console.WriteLine("Минимальный элемент массива:" + m);

Console.ReadKey();
int Min(int[] a, int min, int i = 0)

{

if (i >= N)

return min;

if (min > a[i])

return Min(a, a[i], i + 1);

else

return Min(a, min, i + 1);

}

}

}

}

Скриншот результата работы программы представлен на рисунке 78.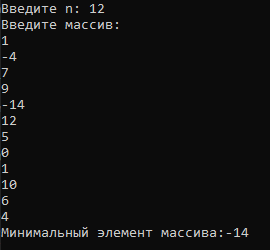



Рисунок 77. Скриншот результата работы программы задачи 8.
Задача 9. Найдите НОД трёх чисел. Примечание: НОД(а,в,с)= НОД(НОД(а,в),с). НОД находите по определению.

Все используемые идентификаторы представлены в таблице 40

Таблица 40 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
A, B, C	A, B, C	integer	Исходные числа, задаются с клавиатуры
Результирующие данные
nod	nod	integer	Результат вычислений

Блок схема алгоритма решения задачи представлена на рисунке 79.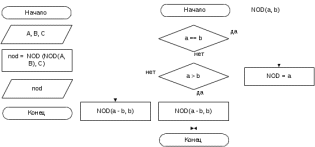



Рисунок 78. Блок схема алгоритма решения задачи 9
Программа на C#:

using System;
namespace lr7_z9

{

class Program

{

static void Main(string[] args)

{

int NOD(int a, int b)

{

if (a == b) return a;

if (a > b)

return NOD(a - b, b);

else

return NOD(b - a, a);

}
Console.Write("Введите a: ");

int A = int.Parse(Console.ReadLine());

Console.Write("Введите b: ");

int B = int.Parse(Console.ReadLine());

Console.Write("Введите c: ");

int C = int.Parse(Console.ReadLine());

int nod = NOD(NOD(A, B), C);

Console.WriteLine("НОД({0}, {1}, {2}) = {3}", A, B, C, nod);

Console.ReadKey();

}

}

}

Скриншот результата работы программы представлен на рисунке 80.



Рисунок 79. Скриншот результата работы программы задачи 9.
Задача 10. Проверьте, являются ли два данных числа взаимно простыми.

Все используемые идентификаторы представлены в таблице 41

Таблица 41 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
A, B	A, B	integer	Исходные числа, задаются с клавиатуры
Результирующие данные
nod	nod	integer	Результат вычислений

Блок схема алгоритма решения задачи представлена на рисунке 81.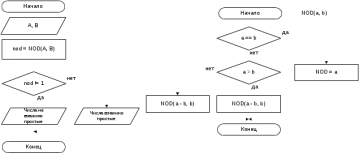



Рисунок 80. Блок схема алгоритма решения задачи 10

Программа на C#:

using System;
namespace lr7_z10

{

class Program

{

static void Main(string[] args)

{

int NOD(int a, int b)

{

if (a == b) return a;

if (a > b)

return NOD(a - b, b);

else

return NOD(b - a, a);

}

Console.Write("Введите A: ");

int A = int.Parse(Console.ReadLine());

Console.Write("Введите B: ");

int B = int.Parse(Console.ReadLine());

if (NOD(A, B) != 1)

Console.Write("Числа не взаимно простые");

else

Console.Write("Числа взаимно простые");

Console.ReadKey();

}

}

}

Скриншот результата работы программы представлен на рисунке 82.



Рисунок 81. Скриншот результата работы программы задачи 10.

Задача 11. Найдите наименьшее общее кратное двух чисел. НОК(n,m)=n*m/НОД(n,m).

Все используемые идентификаторы представлены в таблице 42

Таблица 42 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
A, B	A, B	integer	Исходные числа, задаются с клавиатуры
Промежуточные данные
NOD	NOD	integer	НОД чисел
Результирующие данные
nok	nok	integer	НОК чисел

Блок схема алгоритма решения задачи представлена на рисунке 83.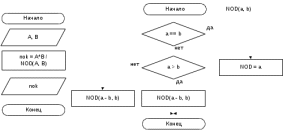



Рисунок 82. Блок схема алгоритма решения задачи 11

Программа на C#:

using System;
namespace lr7_z11

{

class Program

{

static void Main(string[] args)

{

int NOD(int a, int b)

{

if (a == b) return a;

if (a > b)

return NOD(a - b, b);

else

return NOD(b - a, a);

}
Console.Write("Введите A: ");

int A = int.Parse(Console.ReadLine());

Console.Write("Введите B: ");

int B = int.Parse(Console.ReadLine());

int nok = A * B / NOD(A, B);

Console.Write("НОК({0}, {1}) = {2}", A, B, nok);

Console.ReadKey();

}

}

}

Скриншот результата работы программы представлен на рисунке 84.



Рисунок 83. Скриншот результата работы программы задачи 11.

Задача 12. Написать вариант алгоритма Евклида, основанный на соотношениях:

НОД(2*а, 2*b)= 2*НОД(a,b);

НОД(2*a,b) = НОД(a,b), при нечётном b, не включающий деления с остатком, а использующий лишь деление на 2 и проверку чётности.

Все используемые идентификаторы представлены в таблице 43

Таблица 43 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
A, B	A, B	integer	Исходные числа, задаются с клавиатуры
Результирующие данные
nod	nod	integer	Результат вычислений

Блок схема алгоритма решения задачи представлена на рисунке 85.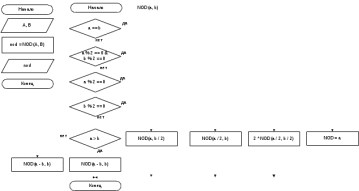



Рисунок 84. Блок схема алгоритма решения задачи 12

Программа на C#:

using System;
namespace lr7_z12

{

class Program

{

static void Main(string[] args)

{

int NOD(int a, int b)

{

if (a == b) return a;

if (a % 2 == 0 && b % 2 == 0)

return 2* NOD(a / 2, b / 2);

if (a % 2 == 0)

return NOD(a / 2, b);

if (b % 2 == 0)

return NOD(a, b / 2);

if (a > b)

return NOD(a - b, b);

else

return NOD(b - a, a);

}

Console.Write("Введите А: ");

int A = int.Parse(Console.ReadLine());

Console.Write("Введите В: ");

int B = int.Parse(Console.ReadLine());

Console.Write("НОД({0}, {1}) = {2}", A, B, NOD(A, B));

Console.ReadKey();

}

}

}

Скриншот результата работы программы представлен на рисунке 86.



Рисунок 85. Скриншот результата работы программы задачи 12.
Задача 13. Вводится последовательность чисел. Вывести их в обратном порядке.

Все используемые идентификаторы представлены в таблице 44

Таблица 44 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
N	N	integer	Количество элементов в массиве
mas	mas	integer[]	Исходный массив
Промежуточные данные
numbers	numbers	integer[]	Массив в рекурсивной функции
i	i	integer	Позиция текущего числа

Блок схема алгоритма решения задачи представлена на рисунке 87.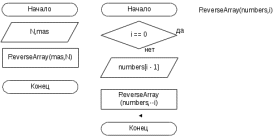



Рисунок 86. Блок схема алгоритма решения задачи 13

Программа на C#:

using System;
namespace lr7_z13

{

class Program

{

static void Main(string[] args)

{

void ReverseArray(int[] numbers, int i)

{

if (i == 0)

return;

Console.Write(numbers[i - 1] + " ");

ReverseArray(numbers, --i);

}

Console.Write("Введите количество чисел: ");

int N = Convert.ToInt32(Console.ReadLine());

Console.WriteLine("Введите числа: ");

int[] mas = new int[N];

for (int i = 0; i < N; i++)

mas[i] = Convert.ToInt32(Console.ReadLine());

Console.Write("Числа в обратном порядке: ");

ReverseArray(mas, N);

Console.ReadKey();

}

}

}

Скриншот результата работы программы представлен на рисунке 88.



Рисунок 87. Скриншот результата работы программы задачи 13.
Задача 14. Напишите рекурсивную программу вычисления n-го члена геометричес­кой прогрессии (b_n= b₁q^n-1), суммы её n первых членов (рекурсивно) и суммы ее членов, начиная с i-гo по k-ый.

Все используемые идентификаторы представлены в таблице 45

Таблица 45 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
n	n	integer	Количество членов прогрессии
b1	b1	integer	Первый член прогрессии
q	q	integer	Знаменатель прогрессии
i, k	i, k	integer	Предельные члены для подсчета суммы
Промежуточные данные
c	c	integer	Номер текущего члена прогрессии
cur	cur	integer	Текущий член прогрессии
Результирующие данные
m		integer	Найденный член прогрессии
s1	s1	double	Сумма членов с 1 по n
s2	s2	double	Сумма членов с i по k

Блок схема алгоритма решения задачи представлена на рисунке 89.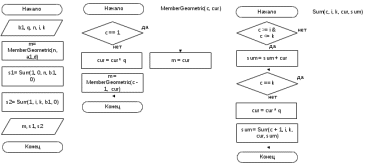

Рисунок 88. Блок схема алгоритма решения задачи 14

Программа на C#:

using System;
namespace lr7_z14

{

class Program

{

static void Main(string[] args)

{

Console.Write("Введите b1 : ");

int b1 = int.Parse(Console.ReadLine());

Console.Write("Введите q: ");

int q = int.Parse(Console.ReadLine());

Console.Write("Введите n: ");

int n = int.Parse(Console.ReadLine());

Console.WriteLine("b[{0}] = {1}", n, MemberGeometric(n, b1));

double s1 = Sum(1, 0, n, b1, 0);

Console.WriteLine("S[{0}] = {1}", n, s1);

Console.Write("Введите i: ");

int I = int.Parse(Console.ReadLine());

Console.Write("Введите k: ");

int K = int.Parse(Console.ReadLine());

double s2 = Sum(1, I, K, b1, 0);

Console.WriteLine("Сумма членов с {0} по {1} = {2}", I, K, s2);

Console.ReadKey();
double Sum(int c, int i, int k, double cur, double sum)

{

if (c >= i && c <= k)

sum += cur;

if (c == k)

return sum;

else

{

cur *= q;

return Sum(c + 1, i, k, cur, sum); ;

}
}
double MemberGeometric(int c, double cur)

{

if (c == 1)

return cur;

else

{

cur *= q;

return MemberGeometric(c - 1, cur);

}

}
}

}

}

Скриншот результата работы программы представлен на рисунке 90.



Рисунок 89. Скриншот результата работы программы задачи 14.

Задача 15. Описать рекурсивную функцию вычисления максимального числа Фибоначчи, ближайшего к заданному n по недостатку.

Все используемые идентификаторы представлены в таблице 46

Таблица 46 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
n	n	integer	Исходное число, задается с клавиатуры
Промежуточные данные
c1, c2	c1, c2	integer	Текущее и предыдущее числа Фибоначчи
Результирующие данные
f	f	integer	Найденное число

Блок схема алгоритма решения задачи представлена на рисунке 91.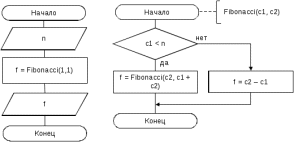



Рисунок 90. Блок схема алгоритма решения задачи 15

Программа на C#:

using System;
namespace lr7_z15

{

class Program

{

static void Main(string[] args)

{

Console.Write("Введите n: ");

int n = int.Parse(Console.ReadLine());

int f = Fibonacci(1, 1);

Console.Write("Найденное число: " + f);

Console.ReadKey();
int Fibonacci(int c1, int c2)

{

if (c1 < n)

return Fibonacci(c2, c1 + c2);

else

return c2 - c1;

}

}

}

}
Скриншот результата работы программы представлен на рисунке 92.



Рисунок 91. Скриншот результата работы программы задачи 15.
Задача 16. Описать рекурсивную функцию поиска индекса минимального элемента массива.

Все используемые идентификаторы представлены в таблице 47

Таблица 47 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
n	n	integer	Количество элементов в массиве, задается с клавиатуры
mas	mas	integer[]	Исходный массив, задается с клавиатуры
Промежуточные данные
i	i	integer	Переменная цикла
a	a	integer[]	Массив в рекурсивной функции
min	min	integer	Текущий индекс минимального элемента
Результирующие данные
min_ind	min_ind	integer	Индекс минимального элемента

Блок схема алгоритма решения задачи представлена на рисунке 93.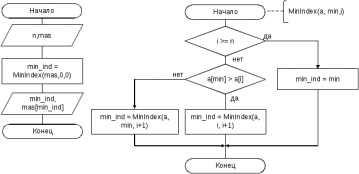



Рисунок 92. Блок схема алгоритма решения задачи 16
Программа на C#:

using System;
namespace lr7_z16

{

class Program

{

static void Main(string[] args)

{

Console.Write("Введите n: ");

int n = Convert.ToInt32(Console.ReadLine());

Console.WriteLine("Введите массив: ");

int[] mas = new int[n];

for (int i = 0; i < n; i++)

mas[i] = Convert.ToInt32(Console.ReadLine());

int min_ind = MinIndex(mas, 0, 0);

Console.WriteLine("Индекс минимального числа = {0}, это число - {1}" , min_ind, mas[min_ind]);

Console.ReadKey();
int MinIndex(int[] a, int min, int i)

{

if (i >= n)

return min;

if (a[min] > a[i])

return MinIndex(a, i, i + 1);

else

return MinIndex(a, min, i + 1);

}

}

}

}

Скриншот результата работы программы представлен на рисунке 94.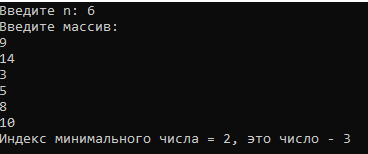



Рисунок 93. Скриншот результата работы программы задачи 16.
Задача 17. Написать функцию, которая находит НОД двух неотрицательных чисел по алгоритму Евклида (второй способ нахождения НОД – делением): Пусть х и у одновременно неравные нулю целые неотрицательные числа и пусть х>=y, тогда если у=0, то НОД(х,у)=х, а если у<>0, то для чисел х, у и r, где r – остаток от деления х на у выполняется равенство: НОД(х,у)= НОД(у,r). (Другими словами: Последний ненулевой остаток, деление на который осуществляется нацело и является НОД чисел х и у)

Например: НОД(48,18)=?

48=18*2+12 (48 делим на 18, остаток 12) 18=12*1+6 (18 делим на 12, остаток 6) 12=6*2+0 (12 делим на 6, остаток 0)

НОД(48,18)= НОД(18,12)= НОД(12,6)=6

Все используемые идентификаторы представлены в таблице 48

Таблица 48 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
A, B	A, B	integer	Исходные числа, задаются с клавиатуры
Результирующие данные
nod	nod	integer	Результат вычислений

Блок схема алгоритма решения задачи представлена на рисунке 95.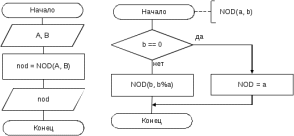



Рисунок 94. Блок схема алгоритма решения задачи 17
Программа на C#:

using System;
namespace lr7_z17

{

class Program

{

static void Main(string[] args)

{

int NOD(int a, int b)

{

if (b == 0)

return a;

else

return NOD(b, a % b);

}

Console.Write("Введите A: ");

int A = int.Parse(Console.ReadLine());

Console.Write("Введите B: ");

int B = int.Parse(Console.ReadLine());

int nod = NOD(A, B);

Console.WriteLine("НОД({0}, {1}) = {2}", A, B, nod);

Console.ReadKey();

}

}

}
Скриншот результата работы программы представлен на рисунке 96.



Рисунок 95. Скриншот результата работы программы задачи 17.
Задача 18. Составить рекурсивную программу, проверяющую, является ли фрагмент строки с i-гo по j-ый символ палиндромом.

Все используемые идентификаторы представлены в таблице 49

Таблица 49 – Идентификаторы

Имя переменной		Тип переменной	Пояснение (возможные ограничения по входным данным, назначение)
алгоритм	программа
Исходные данные
S	S	string	Исходная строка, задается с клавиатуры
i,j	i,j	integer	Индекс начального и конечного символов, задаются с клавиатуры
Промежуточные данные
a,b	a,b	integer	Текущие индексы начального и конечного символов
Результирующие данные
palindrome	palindrome	boolean	Признак палиндрома

Блок схема алгоритма решения задачи представлена на рисунке 97.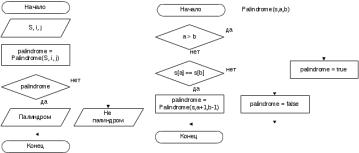



Рисунок 96. Блок схема алгоритма решения задачи 18
Программа на C#:

using System;
namespace lr7_z18

{

class Program

{

static void Main(string[] args)

{

bool Palindrome(string s, int a, int b)

{

if (a > b)

return true;

else

{

if (s[a] == s[b])

return Palindrome(s, a + 1, b - 1);

else

return false;

}

}
Console.Write("Введите строку: ");

string S = Console.ReadLine();

Console.Write("Введите i: ");

int i = int.Parse(Console.ReadLine());

Console.Write("Введите j: ");

int j = int.Parse(Console.ReadLine());

bool palindrome = Palindrome(S, i, j);

if (palindrome)

Console.Write("Строка с {0} по {1} палиндром", i, j);

else

Console.Write("Строка с {0} по {1} не палиндром", i, j);

Console.ReadKey();
}

}

}
Скриншот результата работы программы представлен на рисунке 98.



Рисунок 97. Скриншот результата работы программы задачи 18.