Лабораторная работа асд. Лабораторные работы_по_АСД. Дисциплина Алгоритмы и структуры данных Отчёт по лабораторной работе
 Скачать 3.09 Mb. Скачать 3.09 Mb.
|
Лабораторная работа №7. РекурсияВариант 15 Номер зачётной книжки Задание 1. Используя рекурсию, составить реализацию 18 задач в виде программы на языке программирования и скрин экрана с результатом работы программы. 2. Выполнить анализ работы алгоритмов при задании различных вариантов исходных данных и описать возможные ограничения по входным данным. 3. Составить отчет по выполненной лабораторной работе. Решение Задача 1. Используя рекурсию, составить реализацию 18 задач в виде программы на языке программирования и скрин экрана с результатом работы программы. Все используемые идентификаторы представлены в таблице 32 Таблица 32 – Идентификаторы
Блок схема алгоритма решения задачи представлена на рисунке 63. 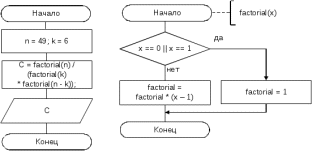 Рисунок 62. Блок схема алгоритма для задачи 1 Программа на C#: using System; namespace lr7_var15_z1 { class Program { static void Main(string[] args) { double factorial(double x) { if (x == 0 || x == 1) return 1; return x * factorial(x - 1); } int n = 49, k = 6; double C = factorial(n) / (factorial(k) * factorial(n - k)); Console.WriteLine("6 из 49 номеров можно выбрать " + C + " способами"); Console.ReadKey(); } } } Скриншот результата работы программы представлен на рисунке 64. Рисунок 63. Скриншот результата работы программы задачи 1. Задача 2. Написать рекурсивную программу, для вычисления аn (возведение целого числа а в целую неотрицательную степень n). Все используемые идентификаторы представлены в таблице 33 Таблица 33 – Идентификаторы
Блок схема алгоритма решения задачи представлена на рисунке 65. 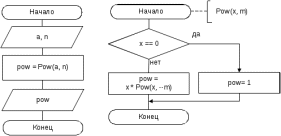 Рисунок 64. Блок схема алгоритма решения задачи 2 Программа на C#: using System; namespace lr7_z2 { class Program { static void Main(string[] args) { double Pow(int x, int m) { if (m == 0) return 1; return x * Pow(x, --m); } Console.Write("Введите a: "); int a = int.Parse(Console.ReadLine()); Console.Write("Введите n: "); int n = int.Parse(Console.ReadLine()); double pow = Pow(a, n); Console.WriteLine("{0}^{1} = {2}", a, n, pow); Console.ReadKey(); } } } Скриншот результата работы программы представлен на рисунке 66. 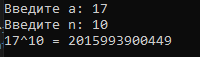 Рисунок 65. Скриншот результата работы программы задачи 2. Задача 3. Написать функцию, которая находит наибольший общий делитель (НОД) двух чисел. 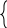 в или а, если а=в НОД(а,в)= НОД(а-в, в), а>в НОД(в-а, а), в>а Это первый способ нахождения наибольшего общего делителя – рекурсивное нахождение НОД вычитанием (по определению). Все используемые идентификаторы представлены в таблице 34 Таблица 34 – Идентификаторы
Блок схема алгоритма решения задачи представлена на рисунке 67. 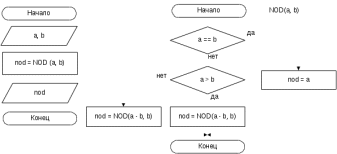 Рисунок 66. Блок схема алгоритма решения задачи 3 Программа на C#: using System; namespace lr7_z3 { class Program { static void Main(string[] args) { int NOD(int a, int b) { if (a == b) return a; if (a > b) return NOD(a - b, b); else return NOD(b - a, a); } Console.Write("Введите первое число: "); int A = int.Parse(Console.ReadLine()); Console.Write("Введите второе число: "); int B = int.Parse(Console.ReadLine()); Console.WriteLine("НОД({0}, {1}) = {2}", A, B, NOD(A, B)); Console.ReadKey(); } } } Скриншот результата работы программы представлен на рисунке 68. 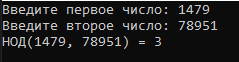 Рисунок 67. Скриншот результата работы программы задачи 3. Задача 4. Составить программу перевода числа из 10-ой системы в n-ичную, где 2<=n<10. Все используемые идентификаторы представлены в таблице 35 Таблица 35 – Идентификаторы
Блок схема алгоритма решения задачи представлена на рисунке 69. 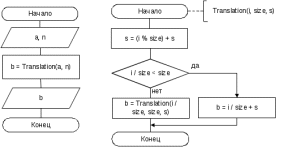 Рисунок 68. Блок схема алгоритма решения задачи 4 Программа на C#: using System; namespace lr7_z4 { class Program { static void Main(string[] args) { string Translation(int i, int size, string s = "") { s = (i % size).ToString() + s; if (i / size < size) return (i / size).ToString() + s; return Translation(i / size, size, s); } Console.Write("Введите число: "); int a = int.Parse(Console.ReadLine()); Console.Write("Введите n: "); int n = int.Parse(Console.ReadLine()); string b = Translation(a, n); Console.Write("Число {0} в системе {1}: {2}", a, n, b); Console.ReadKey(); } } } Скриншот результата работы программы представлен на рисунке 70. 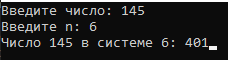 Рисунок 69. Скриншот результата работы программы задачи 4. Задача 5. Написать рекурсивную программу вычисления n-го члена арифметической прогрессии. an=an-1+d Пользователь вводит a1 и d Все используемые идентификаторы представлены в таблице 36 Таблица 36 – Идентификаторы
Блок схема алгоритма решения задачи представлена на рисунке 71. 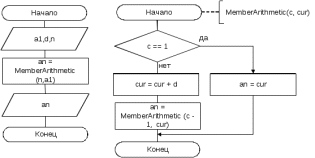 Рисунок 70. Блок схема алгоритма решения задачи 5 Программа на C#: using System; namespace lr7_z5 { class Program { static void Main(string[] args) { Console.Write("Введите a1 : "); int a1 = int.Parse(Console.ReadLine()); Console.Write("Введите d: "); int d = int.Parse(Console.ReadLine()); Console.Write("Введите n: "); int n = int.Parse(Console.ReadLine()); int an = MemberArithmetic(n, a1); Console.Write("a[{0}] = {1}", n, an); Console.ReadKey(); int MemberArithmetic(int c, int cur) { if (c == 1) return cur; else { cur += d; return MemberArithmetic(c - 1, cur); } } } } } т результата работы программы представлен на рисунке 72.  Рисунок 71. Скриншот результата работы программы задачи 5. Задача 6. Написать рекурсивную программу вычисления суммы n первых членов арифметической прогрессии. Все используемые идентификаторы представлены в таблице 37 Таблица 37 – Идентификаторы
Блок схема алгоритма решения задачи представлена на рисунке 73. 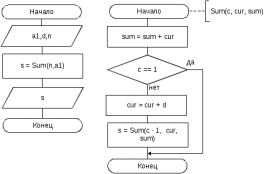 Рисунок 72. Блок схема алгоритма решения задачи 6 Программа на C#: using System; namespace lr7_z6 { class Program { static void Main(string[] args) { Console.Write("Введите a1 : "); int a1 = int.Parse(Console.ReadLine()); Console.Write("Введите d: "); int d = int.Parse(Console.ReadLine()); Console.Write("Введите n: "); int n = int.Parse(Console.ReadLine()); int s = Sum(n, a1); Console.Write("S[{0}] = {1}", n, s); Console.ReadKey(); int Sum(int c, int cur, int sum = 0) { sum += cur; if (c == 1) return sum; else { cur += d; return Sum(c - 1, cur, sum); } } } } } Скриншот результата работы программы представлен на рисунке 74.  Рисунок 73. Скриншот результата работы программы задачи 6. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
