решение задач по финансовой математике. задачи фин.мат. Дисциплина Финансовая математика Текущий контроль знаний по темам Проценты
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Дисциплина «Финансовая математика» Текущий контроль знаний по темам «Проценты», «Финансовые потоки и ренты» Вкладчик положил в банк, выплачивающий 7% в год, вклад 3000 руб. Какова будет сумма на счету вкладчика в конце срока, если вклад оформлен на 3 года 5 месяцев? 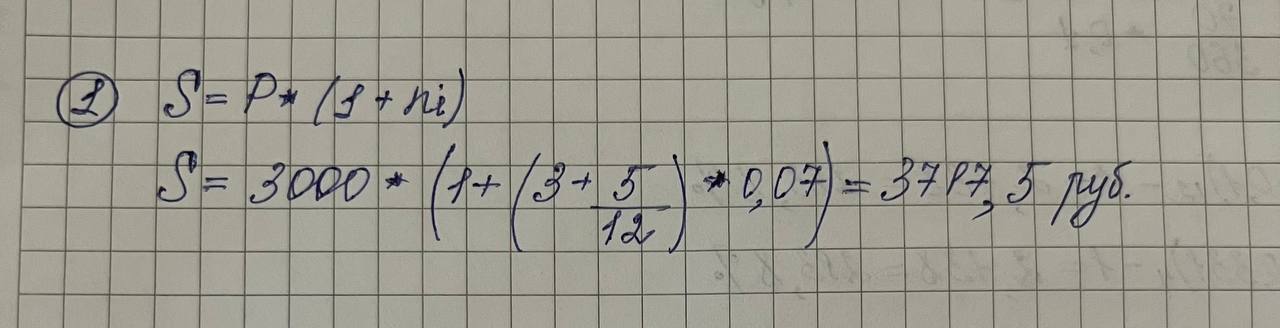 Какую сумму надо положить в банк, выплачивающий 4% в год, чтобы получить 5000 руб. через 2 года 9 месяцев? 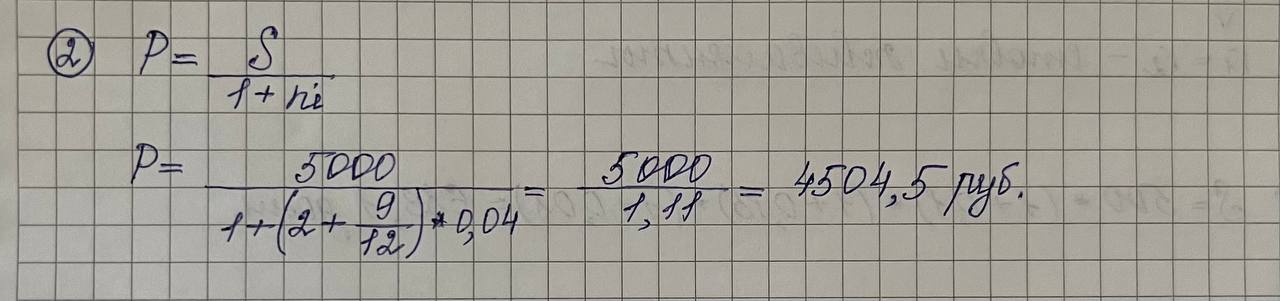 На сколько дней надо положить вклад 6000 руб., чтобы сумма вклада в конце срока составила 6864 руб., если процентная ставка 6% годовых. Правило АСТ/365. 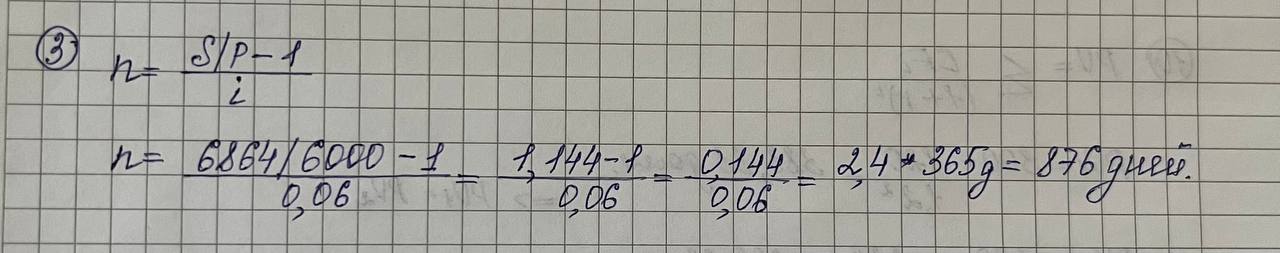 Клиент получил кредит в 6 млн руб. на 3 месяца. Определите простую процентную годовую ставку банка, если сумма погашения кредита 8 млн руб. 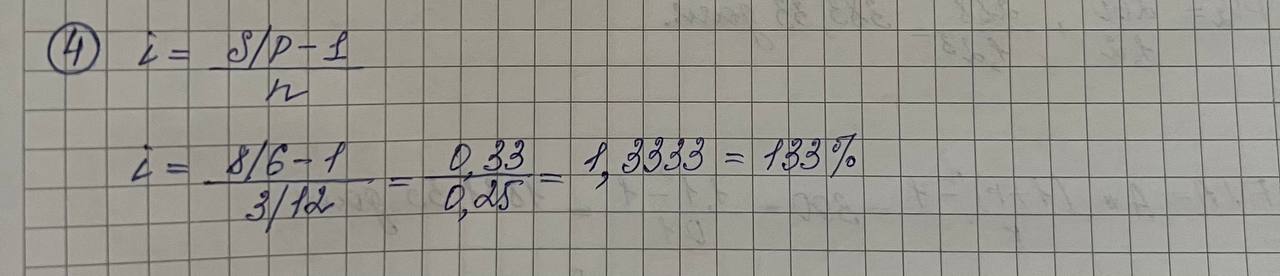 Компания по производству радиоаппаратуры получила в коммерческом банке ссуду на два года под простой дисконт, равный 12% в год. Компания желает получить на руки 90000 руб. Какую сумму она будет должна банку? 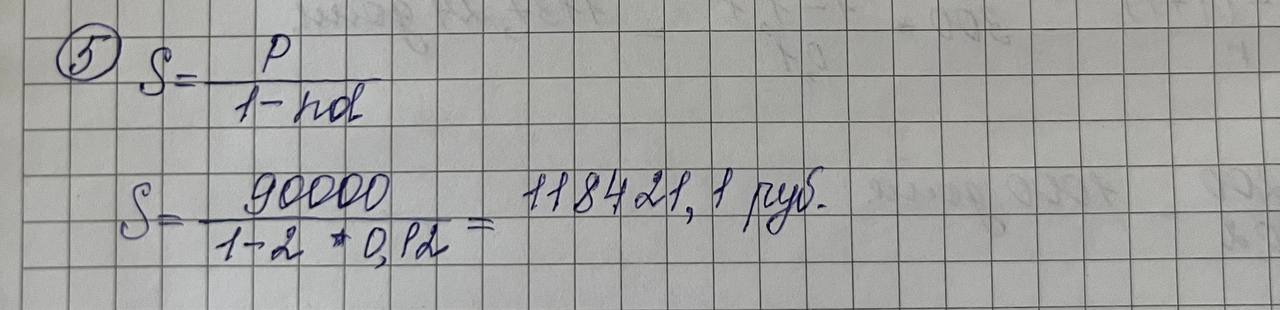 6. На какой срок был выдан кредит в 50 млн руб., если сумма погашения кредита составляет 60 млн руб., а простая учетная ставка 𝑑=210% годовых? 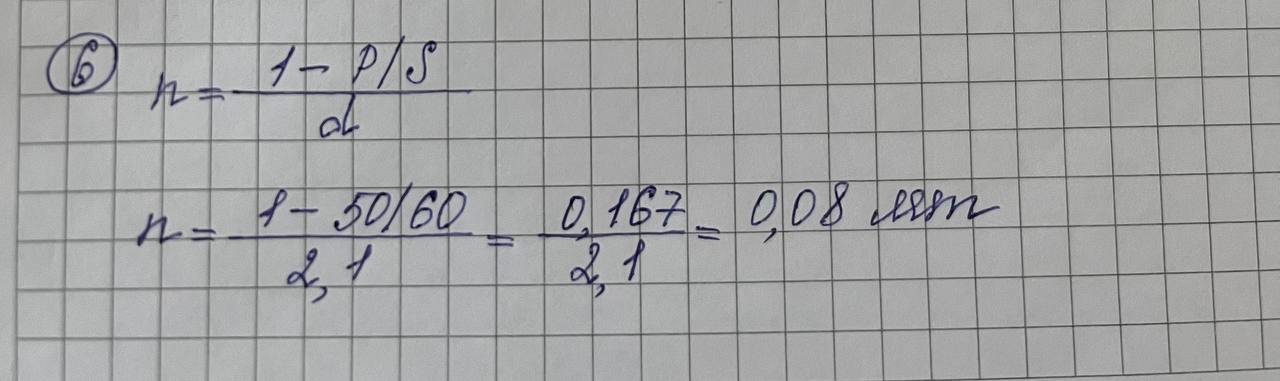 Пусть депозитный сертификат с номиналом 1000 руб., купонной ставкой 15% годовых и сроком обращения 180 дней продан за 70 дней до погашения. Если простая годовая рыночная процентная ставка в момент продажи составляла 10%, то какова цена продажи сертификата? Использовать банковское правило ACT/360. 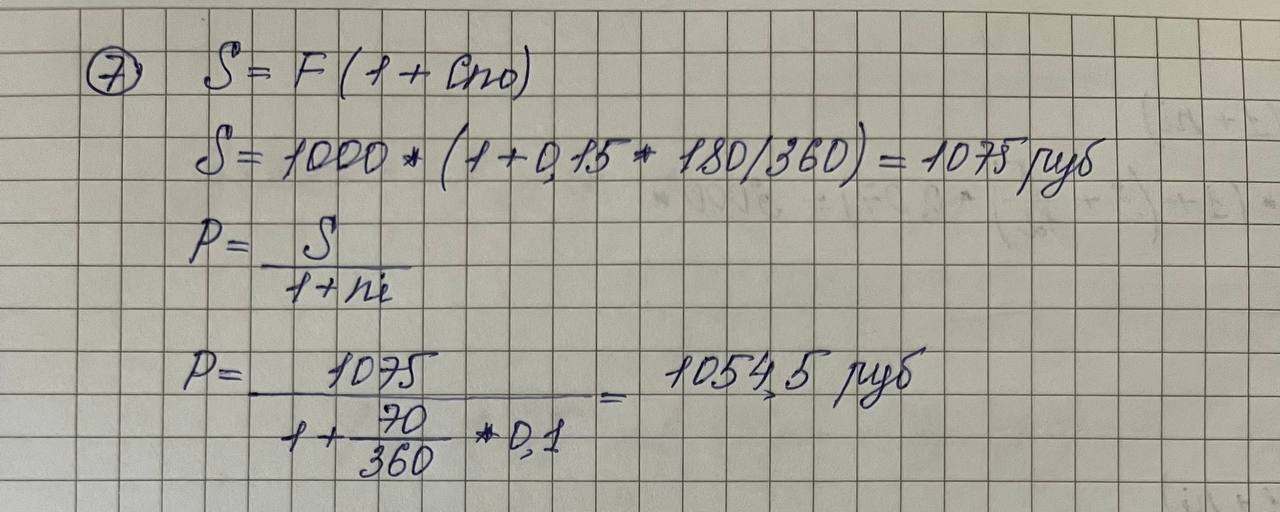 8. Поскольку рыночная ставка 10%, то текущая рыночная цена сертификата будет равна в соответствии с (2.32) 𝑃=10751+0,1⋅70360=1054,50 (руб.). Пусть 𝑖1=10% месячная (ℎ1=1/12), а 𝑖2=33,1% квартальная (ℎ2=1/4) ставка начисления. Являются ли эквивалентными эти ставки?  Пусть банк выплачивал проценты по накопительным вкладам в размере 10% годовых в течение первого года, 15% годовых – в течение второго года и 8% годовых – в течение третьего года. Все ставки фактические. Если вкладчик имел на счету в начале первого года 500 долл., то какова величина вклада в конце каждого года?  Показать, что потоки 𝑪𝑭1={(0,300),(2,120)} и 𝑪𝑭2={(1,260),(3,288)} эквивалентны относительно ставки 𝑖=20%. 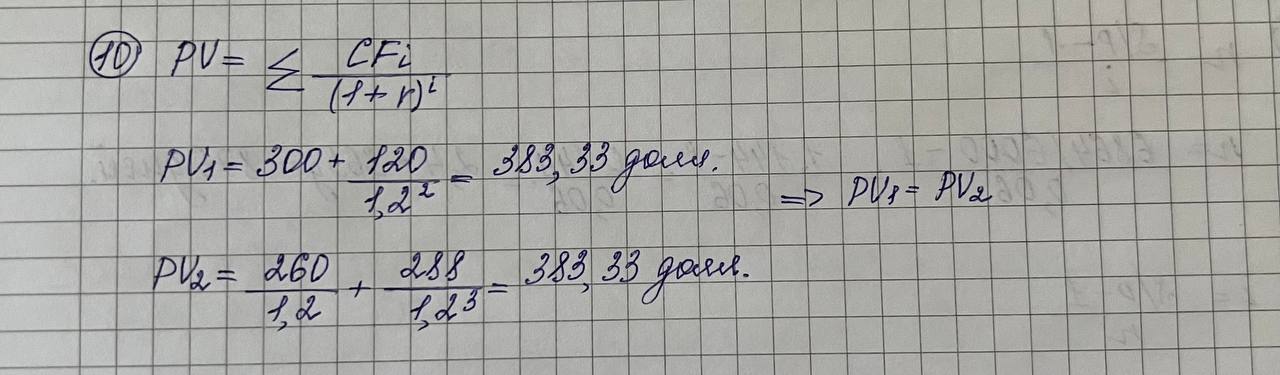 Рассмотрим 5-летнюю обыкновенную ренту с годовыми платежами по 300 долл. Найти накопленную и текущую стоимости этой ренты для квартальной процентной ставки 10%. 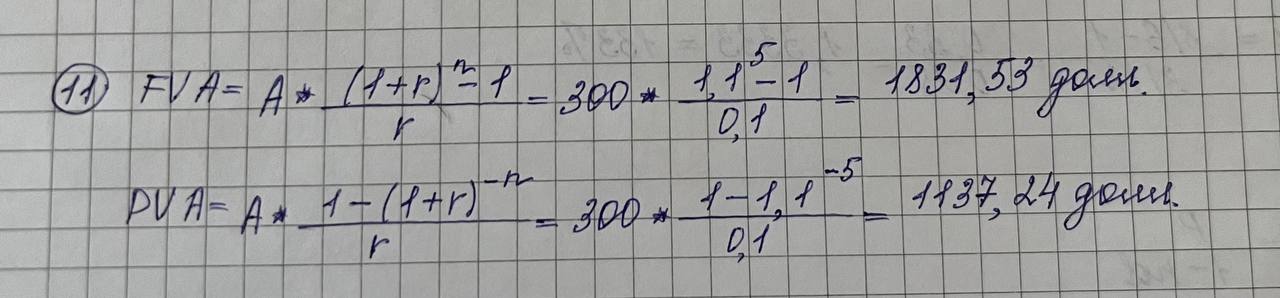 Найти текущую стоимость обыкновенной вечной ренты с ежегодными платежами по 200 долл. при непрерывно начисляемой годовой ставке 𝑗=20%. 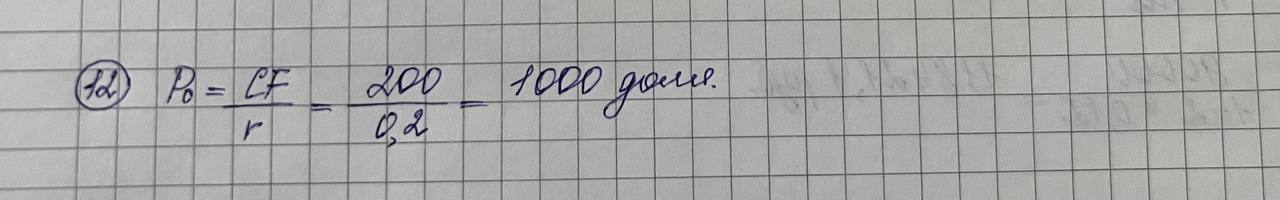 |
