практическая работа. Дисциплина Высшая математика Рамазанов Вадим Рамилович 38. 03. 02 Менеджмент в нефтегазовом комплексе
 Скачать 28.6 Kb. Скачать 28.6 Kb.
|
|
Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий» Зачетная работа 1 семестра Дисциплина: Высшая математика Выполнил: Рамазанов Вадим Рамилович 38.03.02 «Менеджмент в нефтегазовом комплексе» Группа МН – 1221(2) Проверил(а): _____________________________ (Ф.И.О. преподавателя) _____________________________ (дата) Омск 2022г ВАРИАНТ 6. 1.Найти матрицу D= AB-2C A= 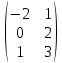 , B= , B= 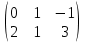 , C= , C= 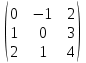 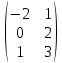 * *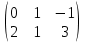 -2 -2 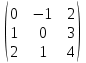 = =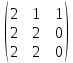 2. Дана невырожденная матрица A. Найти обратную матрицу 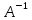 и пользуясь правилом умножения матриц, показать, что A* и пользуясь правилом умножения матриц, показать, что A*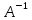 =E , где E – единичная матрица. =E , где E – единичная матрица.A= 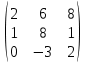 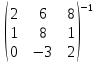 = =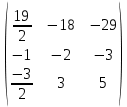 ; ;A= 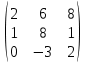 * *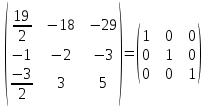 3. Решить системы линейных уравнений с тремя неизвестными. 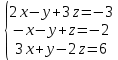 ∆= 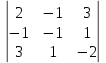 =7; =7;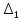 = =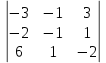 =7; =7;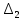 = =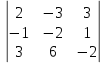 =-7; =-7;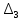 = =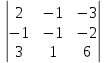 =-14 =-14x= 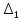 / /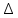 = =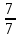 =1 =1y= 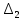 / / = =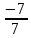 =-1 =-1z= 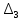 / /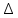 = =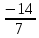 =-2 =-2Ответ: x=1 y=-1 z=-2 4. Построить треугольник, вершины которого находятся в точках A 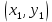 , B , B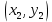 , C , C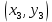 . Найти: . Найти: 1) уравнения сторон треугольника ABC; 2) координаты точки М пересечения медиан; 3) длину и уравнение высоты, опущенной из вершины A; 4) площадь треугольника. A1;3 , B 5; 2 , C5;3. 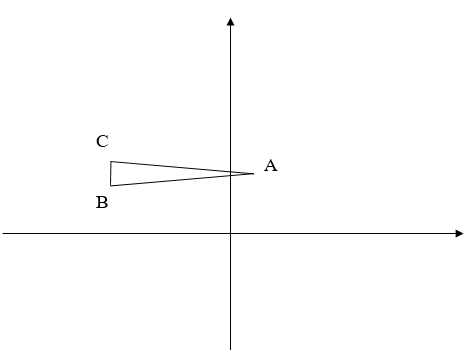 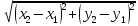 AB| = 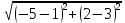 = =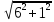 = =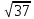 =6.08 =6.08AC|= 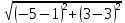 = =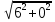 = =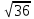 =6 =6BC|= 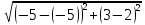 = =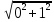 = =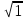 =1 =12. Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 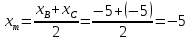 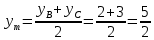 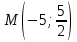 Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(1;3) и М(-5;5/2), поэтому: Каноническое уравнение прямой: 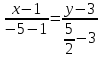 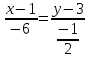 12y-x-35=0 Найдем длину медианы. Расстояние между двумя точками выражается через координаты формулой: |R|= 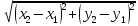 |AM|= 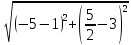 = =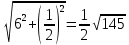 Обозначим середину стороны AC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 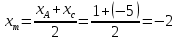 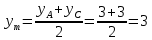 M(-2;3) Уравнение медианы BM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана BМ проходит через точки B(-5;2) и М(-2;3), поэтому: Каноническое уравнение прямой: 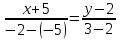 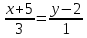 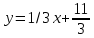 3y-x-11=0 Найдем точку пересечения медиан. Имеем систему из двух уравнений: 12y-x-35=0 3y-x-11=0 Из первого уравнения выражаем y и подставим во второе уравнение. Получаем: x=-3 y= 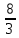 3. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 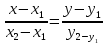 Уравнение прямой BC Каноническое уравнение прямой: 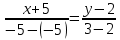 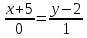 X+5=0 X=-5 4. Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой: 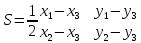 В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна. 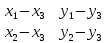 = =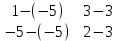 = =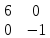 =6*(-1) - 0*0 = -6 =6*(-1) - 0*0 = -6По формуле получаем: 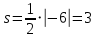 |
