Аналого-цифровые преобразователи. Фурье-Лаплас_Наггов (3). Дискретные преобразования Фурье и Лапласа
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
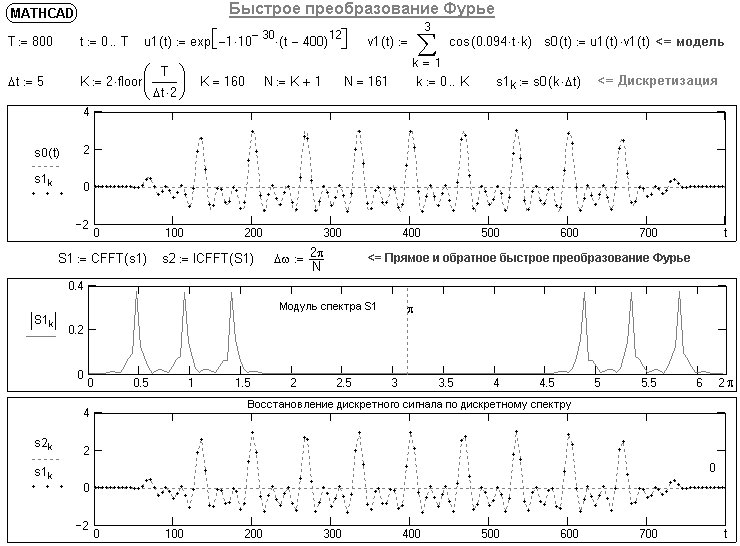 Рис. 1.5. Пример БПФ. Применение ДПФ. Основная область использования ДПФ – спектральный анализ физических данных. При этом интерес обычно представляют только амплитуды отдельных гармоник, а не их фазы, и спектр отображается в виде графика зависимости амплитуды (модуля спектра) от частоты. Часто шкала амплитуд градуируется в децибелах. Децибелы - логарифмы отношения амплитудных значений. Например, разница на 20 дБ означает различие амплитуд в 10 раз, разница на 40 дБ - 100 раз. Различию амплитуд в 2 раза отвечает разница примерно в 6 дБ. Шкала частот также часто градуируется в логарифмическом масштабе. Перед вычислением спектра из сигнала, как правило, вырезается отрезок сигнала. Число последовательных отсчетов отрезка для использования БПФ должно быть степенью двойки, если в программном обеспечении вычислительной системы не оговорена ее способность выполнять БПФ по произвольным числовым рядам. В противном случае числовой ряд дополняется нулями до необходимого размера, что не изменяет формы спектра и сказывается только на увеличении частотного разрешения по спектру. При вычислении спектра возможен следующий нежелательный эффект. При разложении участка сигнала в ряд Фурье мы тем самым принимает этот участок за один период Т, который периодически повторяется за пределами участка с фундаментальной частотой 1/Т. При ДПФ, а равно и при БПФ, вычисляется спектр именно такого периодического сигнала. При этом на границах периодов такая функция наверняка будет иметь разрывы или скачки, тем самым существенно искажая спектр. Для устранения этого эффекта применяются так называемые весовые окна, похожие на гауссиан, размер которых равен размеру участка. Анализируемый участок умножается на весовое окно, что плавно сводят сигнал на нет вблизи краев анализируемого участка и в значительной степени устраняют рассмотренные искажения спектра. Методика применения весовых окон подробно рассматривается в курсе цифровой обработки сигналов. 1.2 Свойства дискретного преобразования Фурье Линейность. Пусть даны две последовательности 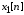 и и 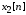 , для которых ДПФ равны соответственно , для которых ДПФ равны соответственно 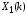 и и 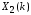 . Спектр взвешенной суммы последовательностей a . Спектр взвешенной суммы последовательностей a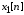 + b + b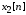 = =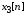 равен аналогичной взвешенной сумме спектров: равен аналогичной взвешенной сумме спектров: = a = a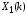 + b + b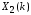 . (1.21) . (1.21)Теорема о свертке. Спектр свертки двух последовательностей 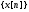 и и  равен произведению спектров равен произведению спектров 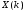 и и 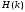 сворачиваемых последовательностей: сворачиваемых последовательностей: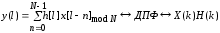 . (1.22) . (1.22)Теорема позволяет вычислить циклическую свертку y[l] при помощи ДПФ по формуле: {y[l]} = ДПФ-1(ДПФ{x[n]} ДПФ{h[n]}) (1.23) ДПФ вещественной последовательности. Пусть {x[n]} – вещественная последовательность. ДПФ такой последовательности имеет следующие особенности: Спектральные коэффициенты комплексно сопряжены относительно N/2 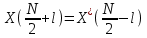 , (1.24) , (1.24)где оператор  означает комплексное сопряжение. означает комплексное сопряжение.Если x[n] – четная последовательность, т.е. x[n]=x[-n], то спектр ДПФ {X(k)} также представляет собой вещественную последовательность. Если x[n] – нечетная последовательность, т.е. x[n]=-x[-n], то {X(k)} представляет собой чисто мнимую последовательность. Данное свойство позволяет при помощи одного преобразования вычислить ДПФ двух действительных последовательностей, либо использовать N/2 –точечное преобразование для вычисления спектра N точечной последовательности. Интерполяция. Спектр последовательности, полученный раздвиганием и дополнением нулями элементов некоторой исходной последовательности, образуется с помощью интерполяции отсчетов ДПФ исходной последовательности. Рассмотрим последовательность g[n], состоящую из MN отсчетов, из них ( M--1) отсчетов являются нулевыми и расположены между отсчетами исходной последовательности x[n]: 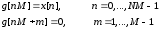 Спектр такой последовательности, с учетом только ненулевых компонент, имеет вид 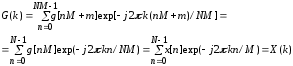 (1.25) (1.25)и представляет повторенный M раз спектр исходной последовательности X(k). Цикличность.Последовательность коэффициентов ДПФ является периодической последовательностью 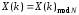 . .Последовательность отсчетов сигнала, полученная обратным ДПФ (ОДПФ) из ее коэффициентов также периодична 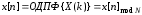 . (1.26) . (1.26)Это свойство следует из периодичности ядра преобразования 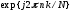 . .2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Полиномиальная запись сигнала давала возможность N-точечную выборку дискретного сигнала представлять в виде единого математического объекта, над которым возможно выполнение различных математических операций по известным правилам. Наряду с ней в математике существует еще одна форма представления функций в виде степенного ряда комплексной переменной z как с положительными, так и отрицательными степенями. Такое представление получило название z-преобразования (его еще называют дискретным преобразованием Лапласа) и может быть использовано для описания и исследования сигналов и его характеристик. Оно относится к классу линейных преобразований, поскольку удовлетворяет всем требованиям линейности. Для действительного сигнала x(i), заданного на бесконечном интервале определения Аналогично записывается z-преобразование и для комплексных сигналов. Функцию X(z) называют z-образом сигнала х(i). Преобразование (2.1) имеет смысл для тех значений z , при которых степенной ряд сходится. Детальное обсуждение вопросов сходимости (2.1) можно найти в [45]. Здесь приведем только ряд общих результатов. Для физических нереализуемых сигналов х(i) , определенных на левом полубесконечном интервале ( т.е. Соотношение (2.2) называют иногда односторонним z-преобразованием. Для финитных сигналов х (i) с Дискретное преобразование Лапласа (ДПЛ), как и ДПФ, может быть получено из интегрального преобразования дискретизаций аргументов (tk = kt, n = n): Y(p) = 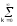 y(tk) exp(-pntk), (2.3) y(tk) exp(-pntk), (2.3)где p = +j- комплексная частота, 0. y(t) = (1/2j) 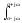 Y(p) exp(pt) dp. y(tk) = t Y(p) exp(pt) dp. y(tk) = t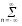 Y(pn) exp(pntk). (2.4) Y(pn) exp(pntk). (2.4)Функцию Y(p) называют изображением Лапласа функции y(t) - оригинала изображения. При = 0 преобразование Лапласа превращается в одностороннее преобразование Фурье, а для каузальных сигналов - в полную аналогию ПФ. Преобразование Лапласа применяется для спектрального анализа функций, не имеющих фурье-образов из-за расходимости интегралов Фурье: Y(p) = 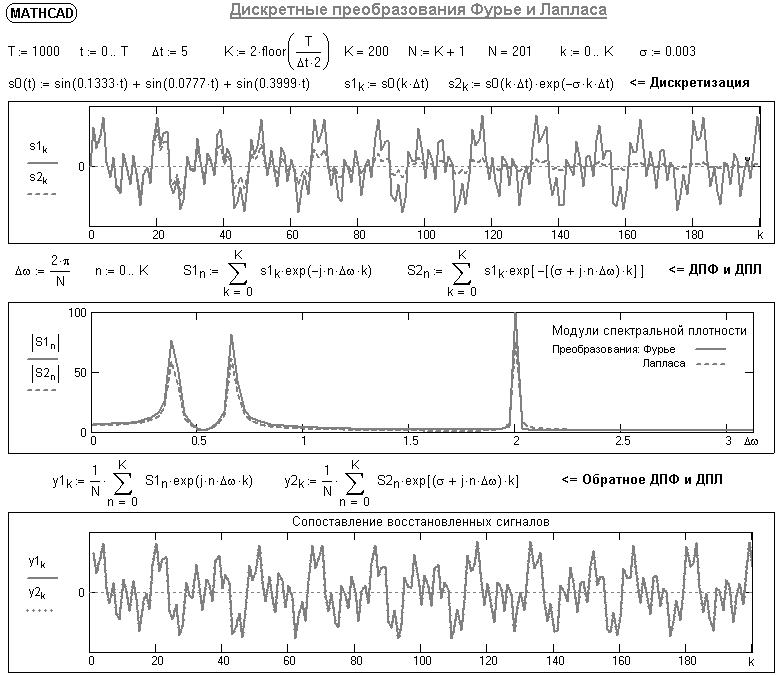 Рис. 2.1. Сопоставление преобразований Фурье и Лапласа. Правый интеграл для каузальных сигналов представляет собой преобразование Фурье, при этом сигнал y'(t) за счет экспоненциального множителя exp(-t) соответствующим выбором значения >0 превращается в затухающий и конечный по энергии. Все свойства и теоремы преобразований Фурье имеют соответствующие аналоги и для преобразований Лапласа. Пример сопоставления преобразований Фурье и Лапласа приведен на рис. 2.1. 3. РАСЧЕТ ПРЕОБРАЗОВАНИЙ ДИСКРЕТИЗИРОВАННЫХ СИГНАЛОВ ФУРЬЕ И ЛАПЛАСА В качестве задания для курсовой работы была дана следующая задача: Дискретный периодический сигнал xд(t) задан отсчетами. В соответствии с вариантом задания (таблица Б.2) вычислите коэффициенты ДПФ Cn. Восстановите аналоговый сигнал x(t) по коэффициентам ДПФ. Убедитесь, что значение сигнала x(t) в отсчетных точках совпадают со значением дискретного сигнала. Период сигнала равен Т. Отсчетные значения сигнала: {1, 2, 1, 1}; Т, с: 2 с. Основной формулой для вычисления коэффициентов ДПФ Сn будет: 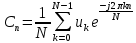 , ,где 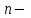 номер коэффициента, номер коэффициента,  число выборок (отсчетов) сигнала, число выборок (отсчетов) сигнала, 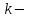 номер отсчета, номер отсчета, 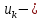 значение отсчета. значение отсчета. В данной задаче нам задано значение периода T равное 2-м секундам. Это позволяет нам вычислить Δt по формуле: T = N/Δt, где Δt будет равно 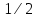 с. Также основным моментом является то, что номер отсчета k равен: k = N-1 = 4-1=3. с. Также основным моментом является то, что номер отсчета k равен: k = N-1 = 4-1=3.Имея все данные, можем подставить их в формулу для вычисления коэффициента ДПФ: 1) 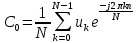 = = 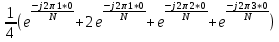 ≈ 1; ≈ 1;2) 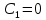 ; ;3) 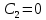 ; ;4) 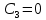 ; ;5) 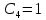 . .Итак, в пределах периода лишь одна спектральная составляющая с амплитудой 1 отлична от нуля. Интересно наглядное подтверждение 3-го свойства ДПФ (цикличности), согласно которому С0 = С4. Если на основании совокупности отсчетов Х0, Х1,.., ХN-1 некоторого сигнала найдены коэффициенты ДПФ С0, С1,.., СN/2, то по ним всегда можно восстановить исходный сигнал x(t) с ограниченным спектром, который был подвергнут дискретизации по следующей формуле: 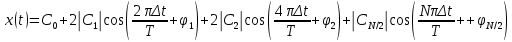 = 1 + 0 + 0 + 0 + cos ( = 1 + 0 + 0 + 0 + cos (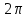 + + 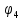 ) = 1 + cos ( ) = 1 + cos (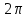 + + 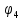 ). ).Таким образом, коэффициенты ДПФ будут равны 1, 0, 0, 0 и 1 соответственно, а при возвращении сигнала в аналоговую форму, получим, что x(t) = 1 + cos ( 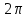 + + 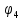 ). ).ЗАКЛЮЧЕНИЕ В моей курсовой работе требовалось описать о том, что представляют из себя дискретные преобразования Фурье и Лапласа, дать их основные определения и понятия об этих преобразованиях. Были даны основные формулы, выводы, а также свойства данных преобразований. Также была поставлена задача вычислить значения коэффициентов ДПФ и по этим коэффициентам требовалось восстановить значение аналогового сигала. Таким образом, благодаря ДПФ удалось рассчитать коэффициенты Cn и по ним восстановить исходный сигнал x(t), с ограниченным спектром. ЛИТЕРАТУРА 1. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с. 2. Гольденберг Л.М. и др. Цифровая обработка сигналов: Учебное пособие для вузов. - М.: Радио и связь, 1990.- 256 с. 3. Канасевич Э.Р. Анализ временных последовательностей в геофизике. - М.: Недра, 1985.- 300 с. 4. Никитин А.А. Теоретические основы обработки геофизической информации: Учебник для вузов. - М.: Недра, 1986.- 342 с. 5. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. – М.: Связь, 1979. – 416 с. 6. Рапопорт М.Б. Вычислительная техника в полевой геофизике: Учебник для вузов. - М.: Недра, 1993.- 350 с. |
