Аналого-цифровые преобразователи. Фурье-Лаплас_Наггов (3). Дискретные преобразования Фурье и Лапласа
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
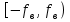 и импульсы выделяются через интервалы и импульсы выделяются через интервалы 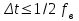 , сдвинутые спектры не перекрываются и центральный (основной) период спектра дискретного сигнала совпадает со спектром исходного непрерывного сигнала. Это означает, что теоретически возможно точно восстановить исходный непрерывный сигнал с помощью идеального фильтра низкой частоты, выделяющего центральный период дискретного спектра. Однако практически точное восстановление дискретного сигнала невозможно и в этом случае, так как для этого требуется создать идеальный фильтр и затратить бесконечное время на интерполяцию, поскольку интерполирующий ряд в этом случае будет содержать бесконечное число членов. , сдвинутые спектры не перекрываются и центральный (основной) период спектра дискретного сигнала совпадает со спектром исходного непрерывного сигнала. Это означает, что теоретически возможно точно восстановить исходный непрерывный сигнал с помощью идеального фильтра низкой частоты, выделяющего центральный период дискретного спектра. Однако практически точное восстановление дискретного сигнала невозможно и в этом случае, так как для этого требуется создать идеальный фильтр и затратить бесконечное время на интерполяцию, поскольку интерполирующий ряд в этом случае будет содержать бесконечное число членов.При разложении дискретных сигналов могут быть использованы только дискретные базисные функции, упорядоченные в конечную базисную систему. Существует два подхода к синтезу дискретных базисных функций. Первый подход состоит в непосредственном формировании дискретных функций, удовлетворяющих условиям упорядоченности, линейной независимости и ортогональности на системе из N точек. Общей методики реализации такого подхода не существует. Известные способы носят частный характер и используют различные разделы целочисленной математики. В §5.5 в качестве примера рассмотрена процедура синтеза дискретной базисной системы с использованием чисел Фибоначчи. Второй подход к синтезу дискретных базисных функций основывается на дискретизации непрерывных базисных функций с сохранением свойств ортогональности и полноты. Для этого подхода характерен ряд общих положений, сформулированных Трахтманом А.М. [59]. Приведем их. Рассмотрим сначала базисную систему, образованную из нечетных непрерывных функций 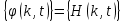 . Поскольку дискретный сигнал задан с помощью . Поскольку дискретный сигнал задан с помощью  отсчетов, то и базисная система отсчетов, то и базисная система 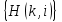 должна также содержать должна также содержать 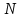 функций функций 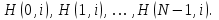 Сумма нечетных функций может образовать только такой сигнал, который имеет нулевой отсчет в точке Сумма нечетных функций может образовать только такой сигнал, который имеет нулевой отсчет в точке 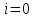 , поэтому нечетный сигнал, по существу, имеет на интервале , поэтому нечетный сигнал, по существу, имеет на интервале 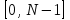 всего всего 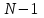 координат. Так как координат. Так как 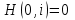 , то и базисная система , то и базисная система 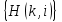 для интервала для интервала 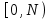 включает в себя, по существу, включает в себя, по существу, 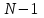 функций. Они могут быть получены путем дискретизации непрерывных функций функций. Они могут быть получены путем дискретизации непрерывных функций 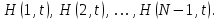 Для этого добавим к этим функциям еще одну функцию с порядком на единицу больше, чем максимальный удерживаемый порядок 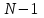 , т.е. функцию , т.е. функцию 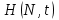 и отметим у нее точки перехода через нуль и отметим у нее точки перехода через нуль 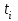 . Тогда дискретная временная ось . Тогда дискретная временная ось 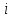 , состоящая из , состоящая из 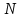 точек, определится нулями функции точек, определится нулями функции 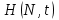 . Возьмем в этих точках отсчеты у всех функций младших порядков и примем их за значения дискретных функций . Возьмем в этих точках отсчеты у всех функций младших порядков и примем их за значения дискретных функций 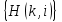 . Полученная после такой дискретизации система дискретных функций будет удовлетворять условию ортогональности . Полученная после такой дискретизации система дискретных функций будет удовлетворять условию ортогональности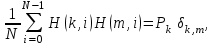 где 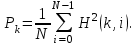 Очевидно, она будет полной системой для множества сигналов, у которых начальный отсчет в точке 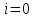 равен нулю. равен нулю.Аналогичная процедура может быть применена и к базисной системе, образованной из четных функций 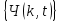 . Соответствующая её полная система ортогональных дискретных четных функций будет состоять из функций . Соответствующая её полная система ортогональных дискретных четных функций будет состоять из функций 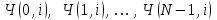 и получается из значений функций и получается из значений функций 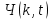 , взятых в моменты времени , взятых в моменты времени 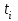 , являющиеся корнями уравнения , являющиеся корнями уравнения 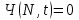 . Эти точки не совпадают с точками, определяющими дискретную временную ось в случае нечетных функций, поэтому временная ось для систем . Эти точки не совпадают с точками, определяющими дискретную временную ось в случае нечетных функций, поэтому временная ось для систем 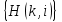 и и 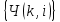 определяется по-разному. определяется по-разному.Полученные таким образом дискретные системы на основе нечетных и четных непрерывных базисных функций пригодны для разложения дискретных сигналов с односторонним полуинтервалом. Для представления дискретных сигналов, определенных на двустороннем или одностороннем полном интервале можно использовать родственные системы, образованные из четных и нечетных функций. При этом любая из родственных дискретных систем (составная, формальная, комплексная) может быть получена с помощью описанной процедуры дискретизации соответствующей непрерывной системы. Для этого из системы непрерывных функций выбираются первые 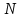 функций функций 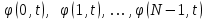 . Затем берется функция следующего старшего порядка . Затем берется функция следующего старшего порядка 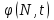 и её нули используются для задания моментов и её нули используются для задания моментов 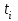 дискретного времени, в которые определяются отсчеты у всех остальных функций. Для составных и комплексных систем такой функцией будет нечетная функция дискретного времени, в которые определяются отсчеты у всех остальных функций. Для составных и комплексных систем такой функцией будет нечетная функция 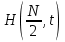 , а для формальных систем – функция , а для формальных систем – функция 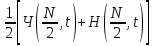 . Следовательно, дискретные временные оси в этих базисных системах будут определены по-разному. Однако, после того, как базисные функции получены, для последующей обработки сигналов это принципиального значения не имеет, так как в дискретных преобразованиях Фурье эти функции используются в виде функций целочисленного аргумента . Следовательно, дискретные временные оси в этих базисных системах будут определены по-разному. Однако, после того, как базисные функции получены, для последующей обработки сигналов это принципиального значения не имеет, так как в дискретных преобразованиях Фурье эти функции используются в виде функций целочисленного аргумента 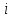 , принимающего значения либо , принимающего значения либо 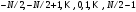 (для симметричного двустороннего интервала), либо (для симметричного двустороннего интервала), либо 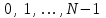 (для одностороннего полного интервала). (для одностороннего полного интервала).Формулы прямого и обратного дискретных преобразований Фурье, мощности базисных функций, условия их ортогональности и равенства Парсеваля для дискретных сигналов и базисных функций с симметричным двусторонним интервалом определения 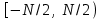 аналогичны приведенным ранее соответствующим формулам для сигналов и функций с односторонним интервалом и отличаются только пределами суммирования. аналогичны приведенным ранее соответствующим формулам для сигналов и функций с односторонним интервалом и отличаются только пределами суммирования.Из рассмотренной методики следует, что при дискретизации непрерывных базисных систем могут быть получены как решетчатые, так и нерешетчатые дискретные базисные системы. Все зависит от расположения нулей функции 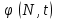 на её интервале ортогональности. Решетчатые системы находят наибольшее применение при спектральной обработке сигналов, поскольку равномерная дискретизация, результатом которой являются решетчатые сигналы, наиболее просто реализуется на практике. Далее в двух последующих главах описанная процедура дискретизации будет использована для получения решетчатых базисных систем на основе некоторых известных непрерывных базисных функций. на её интервале ортогональности. Решетчатые системы находят наибольшее применение при спектральной обработке сигналов, поскольку равномерная дискретизация, результатом которой являются решетчатые сигналы, наиболее просто реализуется на практике. Далее в двух последующих главах описанная процедура дискретизации будет использована для получения решетчатых базисных систем на основе некоторых известных непрерывных базисных функций.Дискретное преобразование Фурье может быть получено непосредственно из интегрального преобразования дискретизаций аргументов (tk = kt, fn = nf): S(f) = 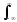 s(t) exp(-j2ft) dt, => S(fn) = t s(t) exp(-j2ft) dt, => S(fn) = ts(t) = 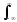 S(f) exp(j2ft) df, => s(tk) = f S(f) exp(j2ft) df, => s(tk) = f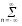 S(fn) exp(j2nftk). (1.15) S(fn) exp(j2nftk). (1.15)Напомним, что дискретизация функции по времени приводит к периодизации ее спектра, а дискретизация спектра по частоте - к периодизации функции. Не следует также забывать, что значения (1.14) числового ряда S(fn) являются дискретизаций непрерывной функции S'(f) спектра дискретной функции s(tk), равно как и значения (1.15) числового ряда s(tk) являются дискретизацией непрерывной функции s'(t), и при восстановлении этих непрерывных функций S'(f) и s'(t) по их дискретным отсчетам соответствие S'(f) = S(f) и s'(t) = s(t) гарантировано только при выполнении теоремы Котельникова-Шеннона. Для дискретных преобразований s(kt) S(nf), и функция, и ее спектр дискретны и периодичны, а числовые массивы их представления соответствуют заданию на главных периодах Т = Nt (от 0 до Т или от -Т/2 до Т/2), и 2fN = Nf (от -fN до fN), где N – количество отсчетов, при этом: f = 1/T = 1/(Nt), t = 1/2fN = 1/(Nf), tf = 1/N, N = 2TfN. (1.16) Соотношения (1.16) являются условиями информационной равноценности динамической и частотной форм представления дискретных сигналов. Другими словами: число отсчетов функции и ее спектра должны быть одинаковыми. Но каждый отсчет комплексного спектра представляется двумя вещественными числами и, соответственно, число отсчетов комплексного спектра в 2 раза больше отсчетов функции? Это так. Однако представление спектра в комплексной форме - не более чем удобное математическое представление спектральной функции, реальные отсчеты которой образуются сложением двух сопряженных комплексных отсчетов, а полная информация о спектре функции в комплексной форме заключена только в одной его половине - отсчетах действительной и мнимой части комплексных чисел в частотном интервале от 0 до fN, т.к. информация второй половины диапазона от 0 до -fN является сопряженной с первой половиной и никакой дополнительной информации не несет. При дискретном представлении сигналов аргумент tk обычно проставляется номерами отсчетов k (по умолчанию t = 1, k = 0,1, … N-1), а преобразования Фурье выполняются по аргументу n (номер шага по частоте) на главных периодах. При значениях N, кратных 2: S(fn) Sn = 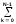 sk exp(-j2kn/N), n = -N/2,…,0,…,N/2. (1.17) sk exp(-j2kn/N), n = -N/2,…,0,…,N/2. (1.17)s(tk) sk = (1/N) 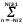 Sn exp(j2kn/N), k = 0,1,…,N-1. (1.18) Sn exp(j2kn/N), k = 0,1,…,N-1. (1.18)Главный период спектра в (1.17) для циклических частот от -0.5 до 0.5, для угловых частот от - до . При нечетном значении N границы главного периода по частоте (значения fN) находятся на половину шага по частоте за отсчетами (N/2) и, соответственно, верхний предел суммирования в (1.18) устанавливается равным N/2. В вычислительных операциях на ЭВМ для исключения отрицательных частотных аргументов (отрицательных значений номеров n) и использования идентичных алгоритмов прямого и обратного преобразования Фурье главный период спектра обычно принимается в интервале от 0 до 2fN (0 n N), а суммирование в (1.18) производится соответственно от 0 до N-1. При этом следует учитывать, что комплексно сопряженным отсчетам Sn* интервала (-N,0) двустороннего спектра в интервале 0-2fN соответствуют отсчеты SN+1-n (т.е. сопряженными отсчетами в интервале 0-2fN являются отсчеты Sn и SN+1-n). Пример: На интервале Т= [0,99], N=100, задан дискретный сигнал s(k) = 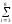 (k-i) - прямоугольный импульс с единичными значениями на точках k от 3 до 8. Форма сигнала и модуль его спектра в главном частотном диапазоне (вычисление по формуле S(n) = (k-i) - прямоугольный импульс с единичными значениями на точках k от 3 до 8. Форма сигнала и модуль его спектра в главном частотном диапазоне (вычисление по формуле S(n) =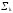 s(k) exp(-j2kn/100) с шагом по частоте =2/100, приведены на рис. 1.1. s(k) exp(-j2kn/100) с шагом по частоте =2/100, приведены на рис. 1.1.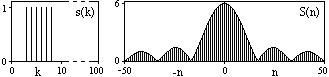 Рис. 1.1. Дискретный сигнал и модуль его спектра. На рис. 1.2 приведена огибающая значений другой формы представления главного диапазона спектра. Независимо от формы представления спектр периодичен, в чем нетрудно убедиться, если вычислить значения спектра для большего интервала аргумента n с сохранением того же шага по частоте, как это показано на рис. 1.3 для огибающей значений спектра. 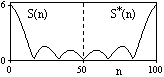 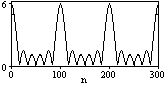 Рис. 1.2. Модуль спектра. Рис. 1.3. Модуль спектра. На рис. 1.4. показано обратное преобразование Фурье для дискретного спектра, выполненное по формуле s'(k) = (1/100)  S(n)exp(j2kn/100), которое показывает периодизацию исходной функции s(k), но главный период k={0,99} этой функции полностью совпадает с исходным сигналом s(k). S(n)exp(j2kn/100), которое показывает периодизацию исходной функции s(k), но главный период k={0,99} этой функции полностью совпадает с исходным сигналом s(k).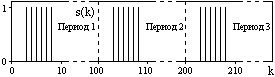 Рис. 1.4. Обратное преобразование Фурье. Преобразования (1.4 - 1.5) называют дискретными преобразованиями Фурье (ДПФ). Для ДПФ, в принципе, справедливы все свойства интегральных преобразований Фурье, однако при этом следует учитывать периодичность дискретных функций и спектров. Произведению спектров двух дискретных функций (при выполнении каких-либо операций при обработке сигналов в частотном представлении, как, например, фильтрации сигналов непосредственно в частотной форме) будет соответствовать свертка периодизированных функций во временном представлении (и наоборот). Такая свертка называется циклической и ее результаты на концевых участках информационных интервалов могут существенно отличаться от свертки финитных дискретных функций (линейной свертки). Из выражений ДПФ можно видеть, что для вычисления каждой гармоники нужно N операций комплексного умножения и сложения и соответственно N2 операций на полное выполнение ДПФ. При больших объемах массивов данных это может приводить к существенным временным затратам. Ускорение вычислений достигается при использовании быстрого преобразования Фурье. 1.1 Быстрое преобразование Фурье Быстрое преобразование Фурье (БПФ). Он базируется на том, что при вычислениях среди множителей (синусов и косинусов) есть много периодически повторяющихся значений (в силу периодичности функций). Алгоритм БПФ группирует слагаемые с одинаковыми множителями в пирамидальный алгоритм, значительно сокращая число умножений за счет исключения повторных вычислений. В результате быстродействие БПФ в зависимости от N может в сотни раз превосходить быстродействие стандартного алгоритма. При этом следует подчеркнуть, что алгоритм БПФ даже точнее стандартного, т.к. сокращая число операций, он приводит к меньшим ошибкам округления. Допустим, что массив чисел sk содержит N = 2r отсчетов (r - целое). Разделим исходный массив на два первых промежуточных массива с четными и нечетными отсчетами: sk' = s2k, sk" = s2k+1, 0 k N/2-1. Выполним ДПФ каждого массива с учетом того, что шаг функций равен 2 (при t=1), а период промежуточных спектров будет соответственно равен N/2: sk' Sn', sk" Sn", 0 n N/2-1. Для получения одной половины искомого спектра Sn сложим полученные спектры с учетом теоремы запаздывания, т.к. отсчеты функции sk" сдвинуты относительно sk' на один шаг дискретизации: Sn = Sn'+Sn"exp(-j2n/N). (1.19) Вторая половина спектра, комплексно сопряженная с первой, с учетом периода повторения N/2 промежуточных спектров определяется выражением: Sn+N/2 = Sn'+Sn"exp(-j2n+N/2)/N) = Sn'- Sn"exp(-j2n/N). (1.20) Нетрудно видеть, что для вычисления полного спектра в данном случае потребуется N2/4 операций для вычисления промежуточных спектров плюс еще N операций комплексного умножения и сложения, что создает ощутимый эффект по сравнению с ДПФ. Но деление массивов на две части может быть применено и к первым промежуточным массивам, и ко вторым, и т.д. до тех пор, пока в массивах не останется по одному отсчету, фурье - преобразование которых равно самому отсчету. Тем самым, алгоритм преобразования превращается в пирамидальный алгоритм перестановок со сложением/вычитанием и с единичным умножением на значение exp(-j2n/N) соответствующего уровня пирамиды. Первый алгоритм БПФ на данном принципе (из множества модификаций, существующих в настоящее время) был разработан Кули-Тьюки в 1965 г. и позволил повысить скорость вычислений в N/r раз по сравнению с ДПФ. Чем больше N, тем больше эффект БПФ. Так, при N = 1024 имеем r = 10 и соответственно N/r 100. Что касается условия по количеству точек N = 2r, то оно рассматривается в варианте Nk 2r, где r - минимальное целое. Массивы с Nk < 2r дополняется до 2r нулями, что не изменяет форму спектра. Изменяется только шаг по представлению спектра (= 2/2r < 2/N), который несколько избыточен по адекватному представлению сигнала в частотной области. В настоящее время существуют и алгоритмы БПФ с другими основаниями и их комбинациями, при которых не требуется дополнения сигналов нулями до 2r. Заметим, что в соответствии с (1.20) отсчеты, сопряженные с правой половиной главного частотного диапазона (0, ), относятся не к диапазону (-,0), а к диапазону (, 2), что, учитывая периодичность спектра дискретных данных, значения не имеет. Т.е. выходной частотный диапазон БПФ равен (0, 2). Общее количество отсчетов комплексного спектра в этом условно главном диапазоне равно количеству точек исходного сигнала (с учетом нулевых точек при дополнении сигнала до N=2r). Алгоритм быстрого обратного преобразования (ОБПФ) тождественен алгоритму прямого БПФ. Алгоритмы прямого и обратного БПФ широко используются в современном программном обеспечении для анализа и обработки цифровых данных. Пример выполнения БПФ приведен на рис. 1.5. |
