Цос 3 лаба. 3_7106_ЗлобинаНИ (3). Дискретное преобразование Фурье
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ТОР отчет по лабораторной работе №3 по дисциплине «ЦОС» Тема: «Дискретное преобразование Фурье»
Санкт-Петербург 2020 Цели работы: - Расчет дискретного преобразования Фурье (ДПФ) средствами MAT-LAB. - Оценка с помощью прямого и обратного ДПФ полосы частот, в которой сосредоточена основная доля энергии сигнала. - Наблюдение изменений результатов вычисления ДПФ, происходящих при дополнении сигнала нулевыми отсчетами. - Оценка степени ускорения вычислений за счет алгоритмов быстрого преобразования Фурье (БПФ). Основные теоретические сведения: Дискретное преобразование Фурье — это разновидность преобразования Фурье, специально предназначенная для анализа дискретных сигналов конечной длительности. При этом данное преобразование определено для периодически продолженного сигнала конечной длительности x(k), k = 0, …, N−1: x(k + N) = x(k) для любого k . (1) Поскольку сигнал (1) является дискретным, его спектр должен быть периодическим с периодом 2π/T, где T — период дискретизации. Так как этот сигнал является также и периодическим, его спектр должен быть дискретным с расстоянием между гармониками, равным 2π/(NT). Далее, если не оговорено иное, предполагается, что период дискретизации равен 1 с. Прямое и обратное ДПФ рассчитываются по следующим формулам: 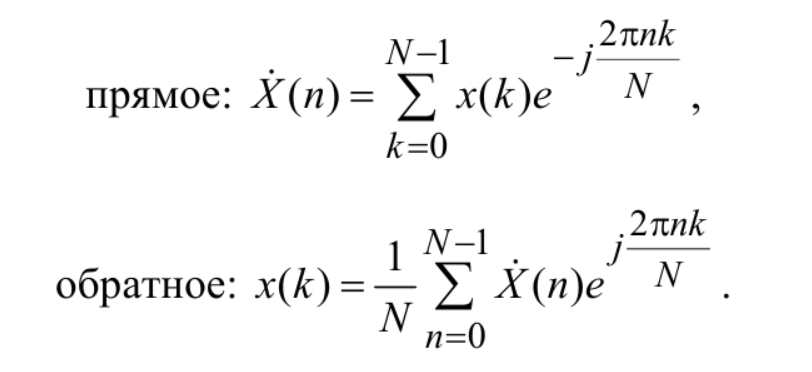 (2) (2)Свойства ДПФ. В целом свойства ДПФ аналогичны свойствам непрерывного преобразования Фурье, однако дискретный характер анализируемого сигнала привносит некоторую специфику. Линейность. ДПФ, согласно определению (2), является линейной комбинацией отсчетов последовательности, поэтому оно подчиняется принципу суперпозиции: Задержка. При задержке сигнала на ∆k отсчетов амплитудный спектр не меняется, а фазовый спектр приобретает дополнительное слагаемое, линейно зависящее от номера гармоники и от значения ∆k: Симметрия. ДПФ вещественного сигнала обладает свойством симметрии: Круговая свертка. Круговой свертке периодических последовательностей соответствует произведение их спектров: 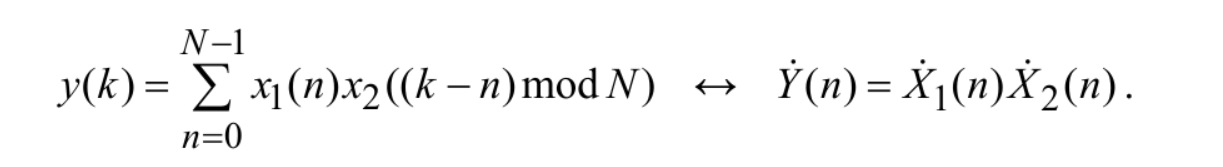 Равенство Парсеваля. Дискретный аналог равенства Парсеваля записывается следующим образом: 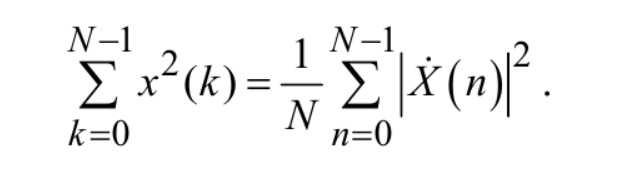 Листинг: %Исходные параметры U = [0 9 9 -8]; % k = [4.5 -4.25]; % b = [0 17.5]; T1=2; T2=6; Fd = 6; % Частота дискретизации, Гц Td = 1/Fd; % Интервал дискретизации t=0:Td:T1; x(1:13)=k(1)*t(1:13); t=0:Td:T2; x(14:37)=k(2)*t(14:37)+b(2); x = [x zeros(1, length(x))]; %---Расчёт ДПФ--- figure subplot(2, 1, 1); spectrum = fft(x); % Вычисление ДПФ f = (-37:1:37); stem(f,abs([spectrum(38:end) spectrum(1:38)])); % АС title('Амплитудный спектр сигнала') xlabel('Отсчеты, k'); ylabel('В*с'); grid on subplot(2, 1, 2); stem(f,angle([spectrum(37:end) spectrum(1:37)])); % ФС title('Фазовый спектр сигнала') xlabel('Осчеты, k'); ylabel('w, рад'); %---Вычисляем энергию спектра исходного сигнала--- Energy = 0; for k = 1:length(x) % Итеративное вычисление энергии temp = abs(x(k))^2; Energy = Energy + temp; end copy_spectrum = spectrum; k = length(copy_spectrum) - ((length(copy_spectrum)-2)/2); m = k; N = 3; % Экспериментально подобранное значение при котором E = 91.3626% for i = 0:((length(copy_spectrum)-2)/2) - N % В этом цикле обнуляем гармоники, которые больше, чем N copy_spectrum(k) = 0; copy_spectrum(m) = 0; k = k + 1; m = m - 1; end figure stem(f, abs([copy_spectrum(38:end) copy_spectrum(1:38)])); % АС title('Амплитудный спектр сигнала после обнуления гармоник') grid on xlabel('Отсчеты, k'); ylabel('В*с'); x_inv = ifft(copy_spectrum); %---График исходного сигнала--- figure subplot(2,1,1); plot(x(1:37)); hold on; stem(x(1:37)); title('Исходный сигнал'); xlabel('Осчеты, k'); ylabel('s(t), B'); %---График восстановленного сигнала--- subplot(2,1,2); stem(x_inv(1:37)); hold on; stem(x(1:37)); title('Исходный и восстановленный сигнал') xlabel('Отсчеты, k'); ylabel('s(t), В'); legend('Восстановленный с','Исходный с'); %-------- Energy_inv = 0; for k = 1:length(x) % Итеративное temp = abs(x_inv(k))^2; % вычисление Energy_inv = Energy_inv + temp; % энергии end disp( [num2str((Energy_inv/Energy)*100) , '%'] ) %----- x_copy = [x zeros(1,length(x))]; % Дополняем нулями сигнал %---Расчёт ДПФ--- figure subplot(2, 1, 1); spectrum_x_copy = fft(x_copy); % Вычисление ДПФ дополненного сигнала f = (-74:1:74); % Ось отсчётов для графика stem(f,abs([spectrum_x_copy(75:end) spectrum_x_copy(1:75)])); %АC title('Амплитудный спектр дополненного нулями сигнала') xlabel('Отсчеты, k'); ylabel('В*с'); subplot(2, 1, 2); stem(f,angle([spectrum_x_copy(75:end) spectrum_x_copy(1:75)]));% ФС title('Фазовый спектр дополненного нулями сигнала') xlabel('Отсчеты, k'); ylabel('w, рад'); %---Измерение скорости расчетов при вычислении ДПФ--- N = 2048; % размер ДПФ % дополнение сигнала нулями до длины N x_test = [x zeros(1, N-length(x))]; D = dftmtx(N); % матрица ДПФ out_test = zeros(1,N); % массив для результатов ДПФ time_array = zeros(1,3); for iterations = 1:3 tic % старт таймера for k = 1:1000 % цикл для измерения времени out_test = x_test * D; % вычисление ДПФ по прямой формуле end time_array(iterations) = toc;% сохранение измеренного времени в массиве end % Вывод усредненного результата disp( [num2str((sum(time_array)*1000)/5) ' мкс.']) %---Измерение скорости с использованием быстрого алгоритма--- N = 1024; % размер ДПФ out_test = zeros(1, N); % массив для результатов ДПФ time_array = zeros(1, 6); for iterations = 1:6 tic % старт таймера for k = 1:100000 % цикл для измерения времени out_test = fft(x, N); % вычисление БПФ end time_array(iterations) = toc; end % Вывод усредненного результата disp( [num2str((sum(time_array)*10)/10) 'мкс.']) 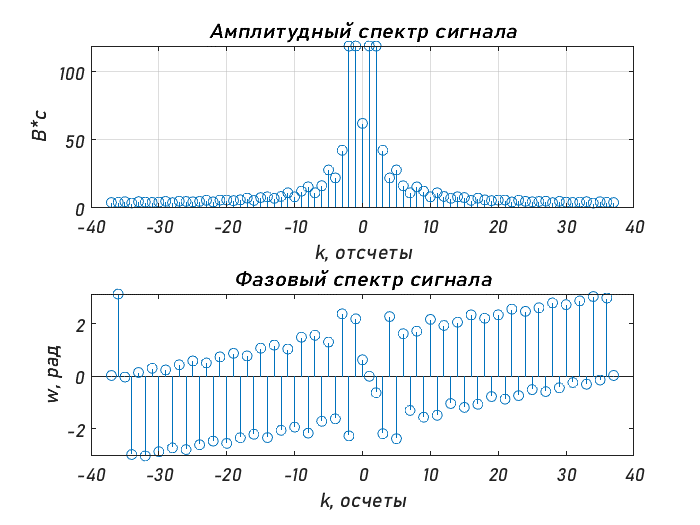 Количество гармоник Nmax= 3. При таком количестве гармоник, энергия сигнала равна 91.3626%. Ширина спектра f=Nmax* Fд/N=3*6000/37 =486.48 Гц. 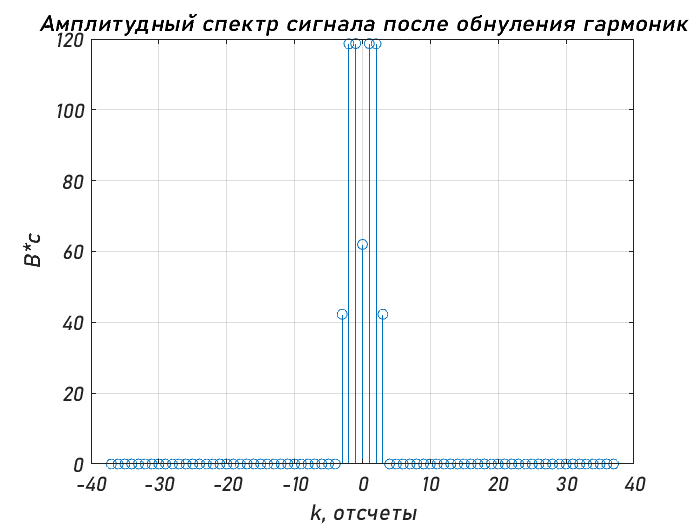 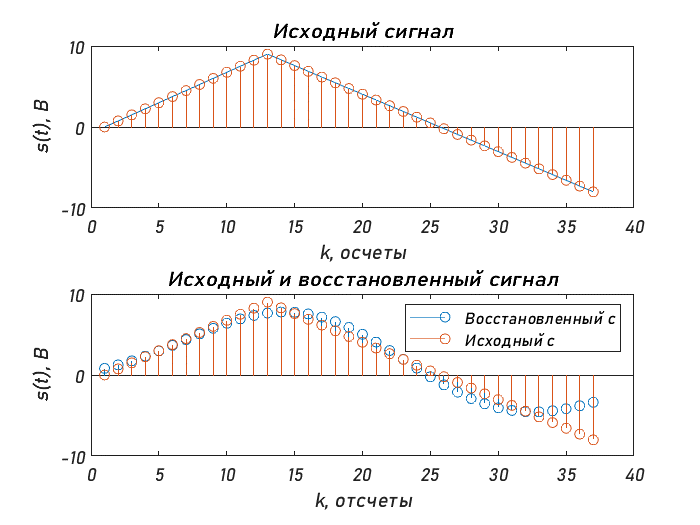 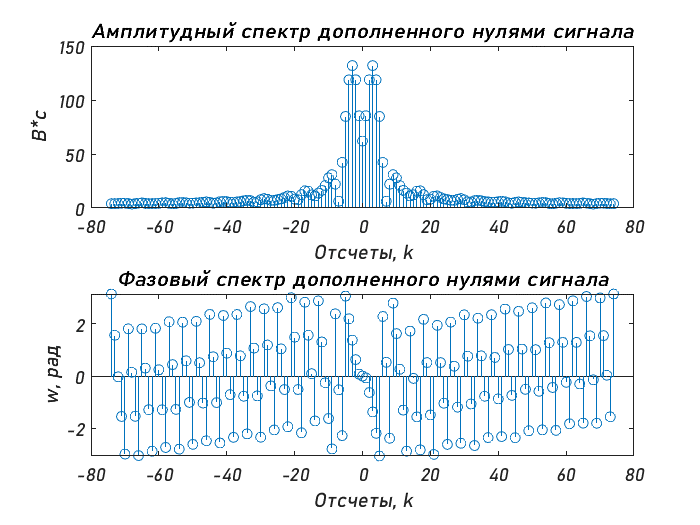 Измерение скорости расчетов при вычислении ДПФ по теоретической формуле и быстрого алгоритма. K=700
К=90000
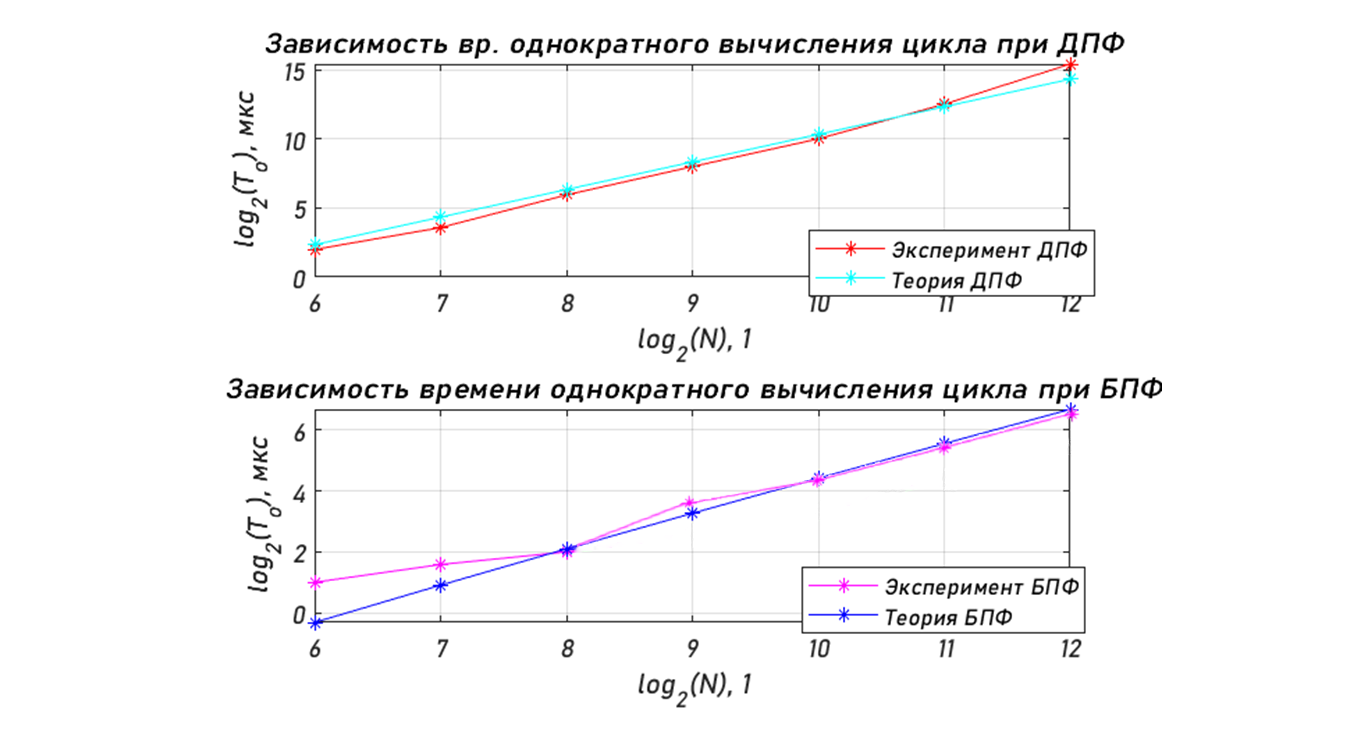 Значение k1 = 0.00136 мкс/ед^2 Значение k2 = 0.00156 мкс/ед^2 Вывод: В ходе выполнения лабораторной работы мы познакомились с методом дискретного преобразования Фурье. Получили АС и ФС нашего сигнала с помощью быстрого преобразования Фурье. Вычислили скорость вычисления спектра с помощью прямого и быстрого метода расчёта ДПФ. Выяснили, что, используя количество отсчётов равного степени двойки можно на порядок увеличить скорость преобразования ДПФ (За счёт использования алгоритма Кули-Тьюки).  Причиной растекания спектра является именно периодическое продолжение анализируемого сигнала. Спектр одиночного фрагмента дискретной синусоиды является периодической непрерывной функцией частоты. Эта функция имеет лепестковую структуру. Однако дискретный ряд частот , на которых вычисляется ДПФ, может быть по-разному расположен относительно лепестков спектральной функции. После увеличения длины сигнала вдвое за счет добавления нулевых отсчетов результат ДПФ стал содержать вдвое больше значений, соответствующих в два раза чаще расположенным частотам Таким образом, дополнение сигнала нулями позволяет более подробно рассмотреть структуру спектра непериодической последовательности отсчетов. Td=10^-4; N=400; t=0:Td:N*Td; s=sin(500*t*2*pi)+sin(525*t*2*pi); subplot (2,2,1); stem(t,s); y=fft(s, N); Mod_s=abs(y); subplot(2,2,2); stem(Mod_s); s1=[s, zeros(1,length(s))]; subplot(2,2,3); stem(s1); s1=fft(s1); Mod_s1=abs(s1); subplot(2,2,4); stem(Mod_s1); 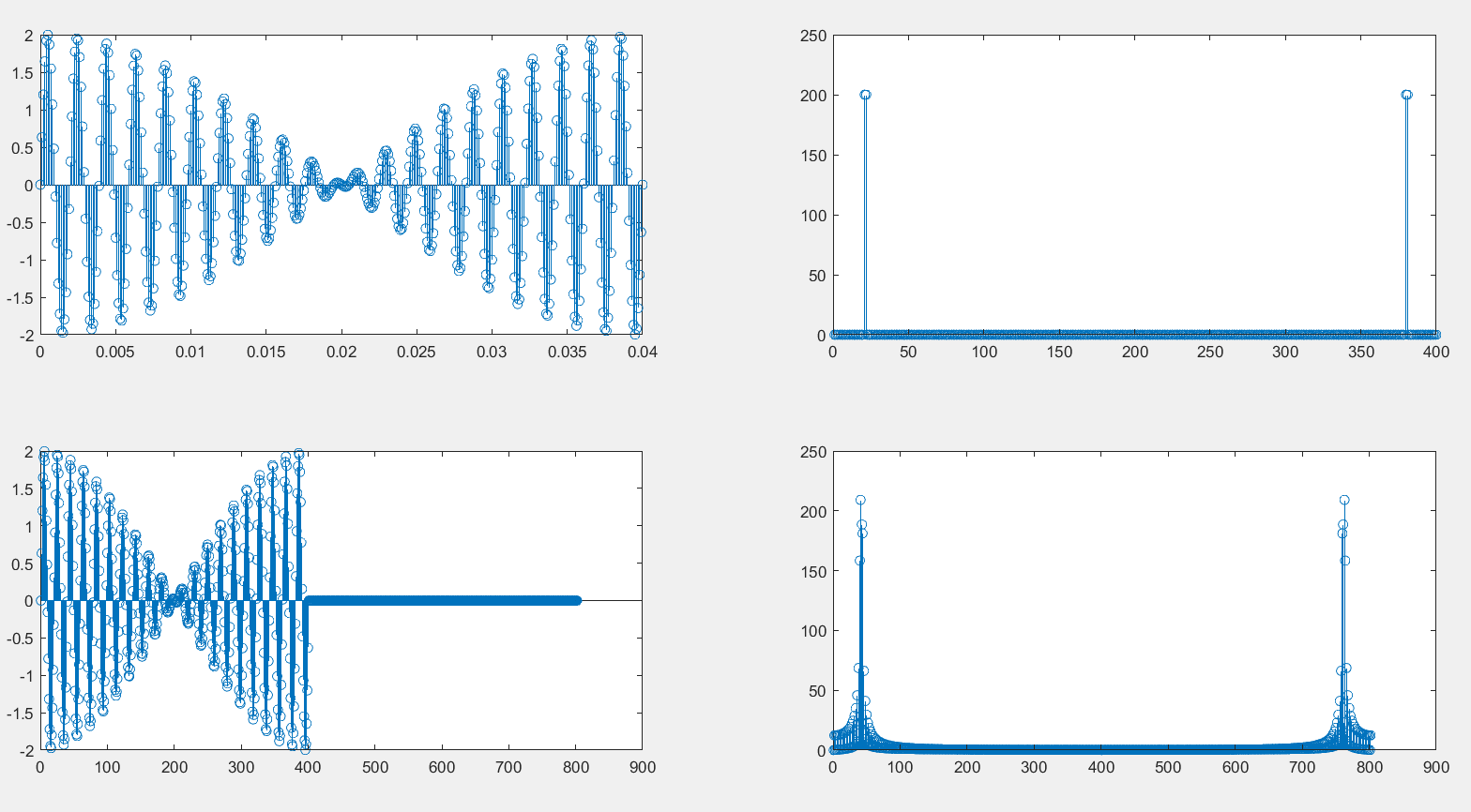 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
