ЛР3 ДПФ. Дискретное преобразование Фурье
 Скачать 370.67 Kb. Скачать 370.67 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра МНЭ отчет по лабораторной работе №3 по дисциплине «Цифровая обработка сигнала» Тема: Дискретное преобразование Фурье
Санкт-Петербург 2021 Цель работы: Выполнить расчет дискретного преобразования Фурье (ДПФ) средствами MATLAB для заданного сигнала. Выполнить оценку с помощью прямого и обратного ДПФ полосы частот, в которой сосредоточена основная доля энергии сигнала. Пронаблюдать изменения результатов вычисления ДПФ, происходящих при дополнении сигнала нулевыми отсчетами. Выполнить оценку степени ускорения вычислений за счет алгоритмов быстрого преобразования Фурье (БПФ). Исходные данные: Таблица 1 - Данные сигнала из лабораторной работы 1
Ход работы: Формирование исходного дискретного сигнала clear all close all clc % Задим параметры дискретного сигнала U1 = -5; U2 = 7; U3 = -3; U4 = 9; t1 = 0.004; t2 = 0.009; F = 4000; dt = 1/F; % Вывод дискретного сигнала t01 = 0: dt: t1 - dt; U = 3000 * t01 - 5; t02 = t1: dt: t2; M = 2400 * t02 - 12.5; Stripe = [U M]; t03 = [t01 t02] % Отрисовка графика дискретного сигнала figure (1) stem(t03, Stripe, 'r'); title('Дискретный сигнал'); xlabel("t, c", 'FontSize', 14); ylabel("U, В", 'FontSize', 14); grid on 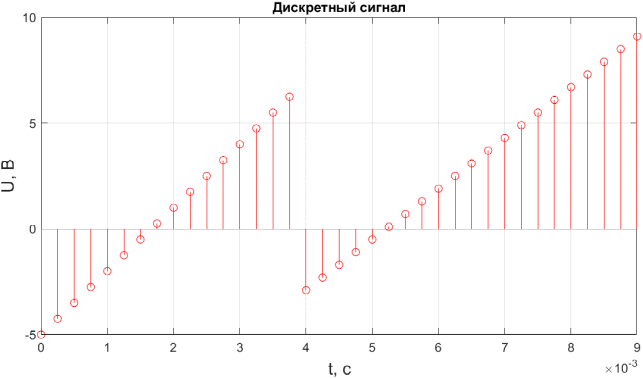 Рисунок 1 – Исходный дискретный сигнал Расчет ДПФ y=fft(Stripe); % Расчет ДПФ Yamp=abs(y); % Амплитудный спектр Ypha=angle(y); % Фазовый спектр % Вывод графиков спектров k = 1: 1: length(t03) figure (2) subplot (2,1,1); stem(k,Yamp); title("Амплитудный спектр", 'FontSize',12); xlabel("k, отсчет", 'FontSize', 14); ylabel("U, B", 'FontSize', 14); subplot (2,1,2); stem(k,Ypha); title("Фазовый спектр", 'FontSize',12); xlabel("k, отсчет", 'FontSize', 14); ylabel("Ф, рад", 'FontSize', 14); 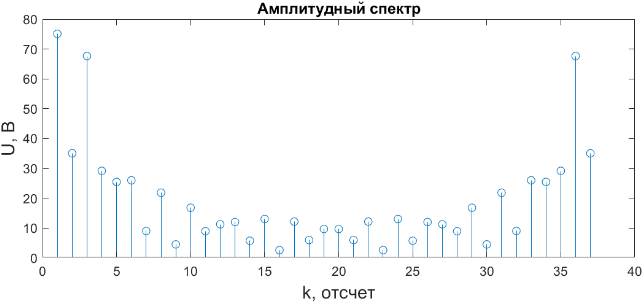 Рисунок 2 – Амплитудный спектр полученного сигнала 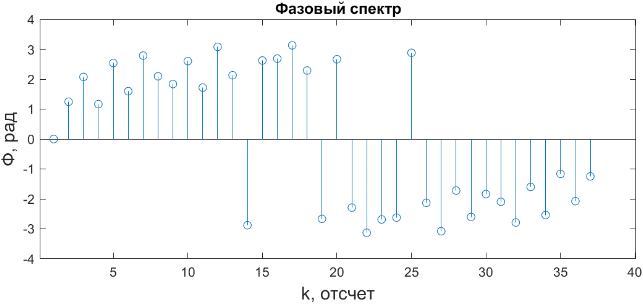 Рисунок 3 – Фазовый спектр полученного сигнала Оценка ширины спектра сигнала % Оценка ширины спектра сигнала E_0 = sum(abs(Stripe).^2); E_check = 0; N_max = -1; while (E_0*0.9) > E_check % Выполняем цикл пока энергия оставшихся гармоник не составит 90% от энергии сигнала N_max = N_max + 1; y_copy=y; y_copy(1 + N_max : end - N_max) = 0; % Обнуляем соответствующие элементы массива ДПФ Stripe_cut = ifft(y_copy); % Вычисляем обратное ДПФ из оставшегося спектра E_check = sum(abs(Stripe_cut).^2); % Вычисляем энергию сигнала с урезанным спектром end % Вывод графиков исходного и преобразованного сигналов figure(3) stem(t03, Stripe); title("График исходнного и преобразованного сигнала") xlabel("t,с"); ylabel("U,В"); hold on stem(t03,Stripe_cut); 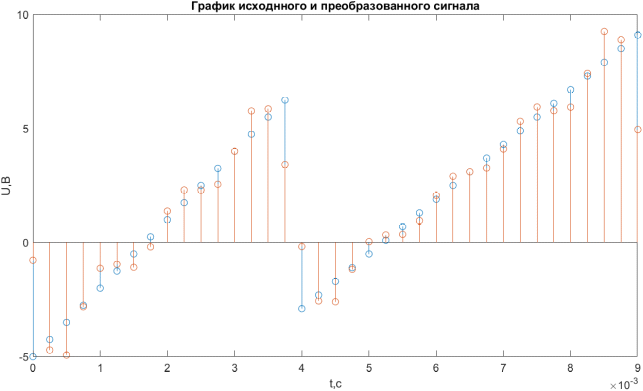 Рисунок 4 – Графики исходного и полученного сигналов Расчетное значение Nmax = 8. Вычислим ширину спектра дискретного сигнала по формуле: 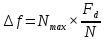 Здесь N – число отсчетов исходного сигнала, Fd – частота дискретизации. Тогда ширина спектра исходного сигнала равна: 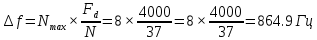 Исследование удлиненного сигнала % Удлинняем сигнал Stripe_copy = [Stripe, zeros(1, length(Stripe))]; t03_2 = 0: dt: (2 * t2) +dt; figure (4) stem(t03_2, Stripe_copy, 'r'); title('Дискретный сигнал (удлиненный)'); xlabel("t, c", 'FontSize', 14); ylabel("U, В", 'FontSize', 14); grid on y_D=fft(Stripe_copy); % Расчет ДПФ Y_D_amp=abs(y_D); % Амплитудный спектр Y_D_pha=angle(y_D); % Фазовый спектр % Вывод графиков спектров k_02 = 1: 1: length(t03_2) figure (5) subplot (2,1,1); stem(k_02,Y_D_amp); title("Амплитудный спектр (удлиненный сигнал)", 'FontSize',12); xlabel("k, отсчет", 'FontSize', 14); ylabel("U, B", 'FontSize', 14); subplot (2,1,2); stem(k_02,Y_D_pha); title("Фазовый спектр (удлиненный сигнал)", 'FontSize',12); xlabel("k, отсчет", 'FontSize', 14); ylabel("Ф, рад", 'FontSize', 14);  Рисунок 5 – Амплитудный спектр удлиненного сигнала 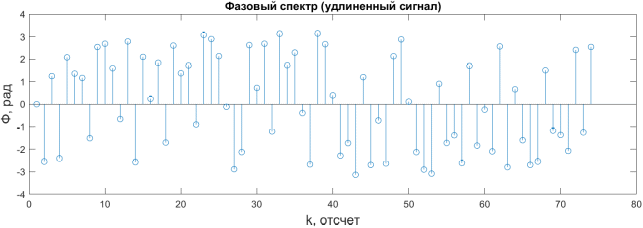 Рисунок 6 – Фазовый спектр удлиненного сигнала Измерение скорости расчетов при вычислении ДПФ по теоретической формуле %Измерение скорости расчетов при вычислении ДПФ по теор. формуле N=64 % Размер ПДФ x1=[Stripe, zeros(1,N-length(Stripe))]; %Дополнение сигнала нулями до длины N D=dftmtx(N); % Матрица ДПФ w = zeros(1,N); % Массив для результатов ДПФ tic% Старт таймера for k = 1:5000 % Цикл для измерения времени w = x1*D; end toc % Отображение измеренного времени Таблица 2 – Затраты времени на расчет ДПФ по теоретической формуле (для 5000 итераций)
Измерение скорости расчетов при вычислении ДПФ с использованием быстрого алгоритма % Измерение скорости расчетов при вычислении ДПФ с исп. быстрого алгоритма N1=8192; % Размер ДПФ q=zeros(1,N1); % Массив для результатов ДПФ tic % Старт таймера for k=1:250000 % Цикл для измерения времени q=fft(Stripe,N1); % Расчет ДПФ end toc % Отображение измеренного времени Таблица 3 – Затраты времени на расчет ДПФ по быстрому алгоритму (для 250000 итераций)
%Вычисление затрат времени на однократный расчет N2=[64 128 256 512 1024 2048 4096 8912]; t_teor=[0.0072 0.0152 0.0341 0.1152 0.7005 9.7211 43.0330 175.2372]; t_fast=[0.1584 0.1741 0.2496 0.3509 0.6822 1.3535 2.6621 5.5105]; t_teor_odin=(t_teor./5000)*1000000; t_fast_odin=(t_fast./250000)*1000000; % Вывод графиков в логарифмическом масштабе figure (6) semilogy (log2(N2),t_teor_odin, 'r'); hold on semilogy (log2(N2),t_fast_odin, 'b'); grid on title('Зависимость для времени вычисления ДПФ и БДПФ', 'FontSize',12); xlabel("log_2(N2)", 'FontSize', 14); ylabel("t ДПФ красный, t БДПФ синий", 'FontSize', 14); semilogy(log2(N2), 0.0005.*(N2.^2), ':r'); semilogy(log2(N2),0.0003.*(N2).*log2(N2), ':b'); hold off 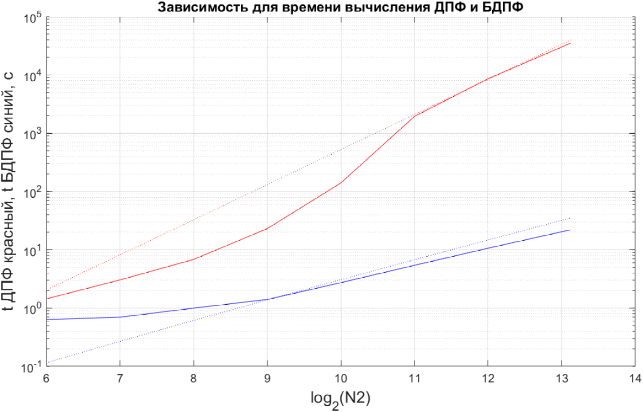 Рисунок 7 – Графики зависимости затрат времени на однократное вычисление ДПФ и БДПФ Вывод: В ходе выполнения работы было произведено вычисление дискретного преобразования Фурье для заданного дискретного сигнала в пакете программ MathLAB. Для заданного сигнала, а также сигнала удлиненного нулевыми отсчетами были вычислены фазовые и амплитудные спектры. Для заданного сигнала была выполнена оценка ширины его спектра при помощи обратного дискретного преобразования Фурье. Вычисленная ширина спектра составила 864,9 Гц. Была выполнена оценка скорости вычисления дискретного преобразования Фурье по теоретической формуле и с использованием быстрого алгоритма, в зависимости от длинны передаваемого сигнала. Для коротких сигналов (≈64 отсчета) быстрый алгоритм работает быстрее примерно в 2,27 раза, а для длинных сигналов (≈8192 отсчета) быстрый алгоритм справляется с задачей в 1593 раза быстрее. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
