ЦОС - ЛР4. Лабораторная работа 4 Дискретное преобразование Фурье периодических и конечных последовательностей
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Федеральное агентство связи Государственное образовательное учреждение высшего профессионального образования Московский Технический Университет Связи и Информатики (МТУСИ) Кафедра радиотехнических систем Лабораторная работа №4 Дискретное преобразование Фурье периодических и конечных последовательностей Выполнила студентка группы БРА1101 Тюрина А.В. Проверила Мирошникова Н.Е. Москва 2013 ЦЕЛИ РАБОТЫ Изучить математическое дискретное преобразование Фурье (ДПФ) периодических последовательностей и последовательностей конечной длины и овладеть программными средствами его вычисления в MATLAB с использованием алгоритмов быстрого преобразования Фурье (БПФ). ИСХОДНЫЕ ДАННЫЕ
ДОМАШНЕЕ ЗАДАНИЕ Вариант 12. 1C. Периодическая последовательность с периодом 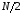 : :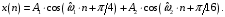 Вывести графики амплитудного и фазового спектра периодической последовательности. Определить амплитуды и частоты дискретных гармоник, используя function-файл fft_e1. function [ output_args ] = Untitled( input_args ) N = 64; Fs = 6000; A1 = 1.12; A2 = 2.24; f1 = 750; f2 = 1500; n = 0:(N-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ k = 0:(N-1); % ДИСКРЕТНАЯ НОРМИРОВАННАЯ ЧАСТОТА w1 = 2*pi*f1/Fs; w2 = 2*pi*f2/Fs; % НОРМИРОВАННЫЕ ЧАСТОТЫ ДИСКРЕТНЫХ ГАРМОНИК (РАД) x = A1*cos(w1*n+pi/4)+A2*cos(w2*n+pi/16); % ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ X = fft(x); % ДПФ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ MOD = (2/N)*abs(X); % АМПЛИТУДНЫЙ СПЕКТР ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ MOD(1) = (1/N)*abs(X(1)); PHASE = angle(X); % ФАЗОВЫЙ СПЕКТР ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ for i = 1:N if (abs(X(i)) < 1e-4) PHASE(i)=0; end end figure('Name','Amplitude Spectrum','NumberTitle', 'off') subplot(2,1,1), stem(k,MOD,'MarkerSize',3,'Linewidth',2), grid xlabel('k'), ylabel('1/N|X(k)|') title(strcat(['Amplitude Spectrum of the Periodic Sequence N = ',num2str(N)])) subplot(2,1,2), stem(k*(Fs/N),MOD,'MarkerSize',3,'Linewidth',2),grid xlabel('f (Hz)'), ylabel('1/N|X(f)|') title(strcat(['Amplitude Spectrum of the Periodic Sequence N = ',num2str(N)])) figure('Name','Phase Spectrum','NumberTitle', 'off') subplot(2,1,1), stem(k, PHASE,'MarkerSize',3,'Linewidth',2), grid xlabel('k'), ylabel('arg{X(k)} (rad)') title(strcat(['Phase Spectrum of the Periodic Sequence N = ',num2str(N)])) subplot(2,1,2), stem(k*(Fs/N),PHASE,'MarkerSize',3,'Linewidth',2) grid, xlabel('f (Hz)'), ylabel('arg{X(f)} (rad)') title(strcat(['Phase Spectrum of the Periodic Sequence N = ',num2str(N)])) disp('% Выходные параметры функции fft_e1') e1 = 1e-7; % ЗНАЧЕНИЕ ПОРОГА ДЛЯ ПЕРВОГО КРИТЕРИЯ [MODm,m] = fft_e1(MOD,e1) % ВНЕШНЯЯ ФУНКЦИЯ ДЛЯ ВЫДЕЛЕНИЯ АМПЛИТУД И ЧАСТОТ ГАРМОНИК ПОЛЕЗНОГО СИГНАЛА ПО ПЕРВОМУ КРИТЕРИЮ A1 = MODm(1); A2 = MODm(2); % АМПЛИТУДЫ ДИСКРЕТНЫХ ГАРМОНИК k1 = m(1); k2 = m(2); % ДИСКРЕТНЫЕ НОРМИРОВАННЫЕ ЧАСТОТЫ f1 = k1*Fs/N; f2 = k2*Fs/N; % ЧАСТОТЫ (Гц) ДИСКРЕТНЫХ ГАРМОНИК disp('% Амплитуды и частоты дискретных гармоник') disp([' A1 = ' num2str(A1) ' A2 = ' num2str(A2)]) disp([' k1 = ' num2str(k1) ' k2 = ' num2str(k2)]) disp([' f1 = ' num2str(f1) ' f2 = ' num2str(f2)]) end 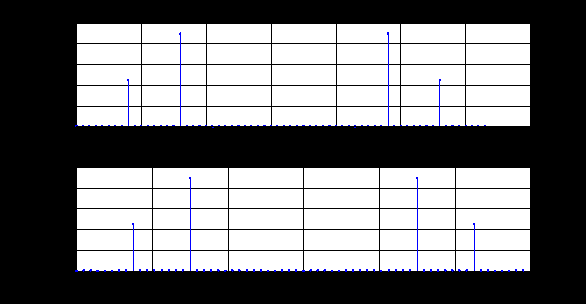 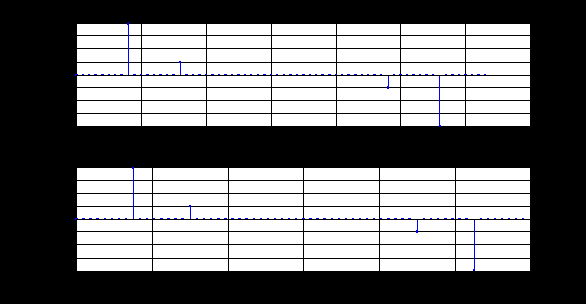 % Выходные параметры функции fft_e1 MODm = 1.1200 2.2400 2.2400 1.1200 m = 8 16 48 56 % Амплитуды и частоты дискретных гармоник A1 = 1.12 A2 = 2.24 k1 = 8 k2 = 16 f1 = 750 f2 = 1500 2С. Конечная последовательность 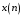 длины длины 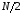 . .Вывести графики модуля и аргумента ДПФ конечной последовательности. function [ output_args ] = Untitled2( input_args ) A1=1.12; A2=2.24; f1=750; f2=1500; N=64; Fs=6000; n = 0:(N-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ k = 0:(N-1); % ДИСКРЕТНАЯ НОРМИРОВАННАЯ ЧАСТОТА w1 = 2*pi*f1/Fs; w2 = 2*pi*f2/Fs; % НОРМИРОВАННЫЕ ЧАСТОТЫ ДИСКРЕТНЫХ ГАРМОНИК (РАД) x = A1*cos(w1*n+pi/4)+A2*cos(w2*n+pi/16); X = fft(x); % ДПФ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ MOD_K = abs(fft(x)); % МОДУЛЬ ДПФ КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ MOD_P = angle(fft(x)); % АРГУМЕНТ ДПФ КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ figure('Name','DFT Modulus and Argument', 'NumberTitle','off') subplot(2,1,1), stem(k,MOD_K,'MarkerSize',3,'Linewidth',2), grid subplot(2,1,2), stem(k,MOD_P,'MarkerSize',3,'Linewidth',2), grid end 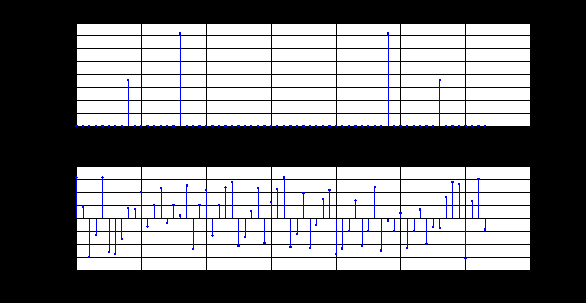 3С. Конечная последовательность длины 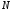 : :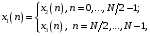 где 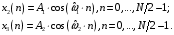 Вывести графики конечных последовательностей 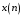 и и 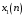 и модулей их ДПФ. и модулей их ДПФ.function [ output_args ] = Untitled3( input_args ) A1=1.12; A2=2.24; N=64; Fs=6000; f1=750; f2=1500; k=0:(N-1); n=0:(N-1); w1=2*pi*f1/Fs; w2=2*pi*f2/Fs; u=0:(N/2-1); c=N/2:(N-1); x1=A1*cos(w1.*u); x2=A2*cos(w2.*c); x=[x1 x2]; Mod_K=abs(fft(x)); Mod_K1=abs(fft(x1)); Mod_K2=abs(fft(x2)); subplot(3,2,5), stem(n,x, 'markersize',3,'Linewidth',2), grid subplot(3,2,6),stem(k,Mod_K, 'markersize',3,'Linewidth',2), grid subplot(3,2,1),stem(u,x1, 'markersize',3,'Linewidth',2), grid subplot(3,2,3),stem(c,x2, 'markersize',3,'Linewidth',2), grid subplot(3,2,2),stem(u,Mod_K1, 'markersize',3,'Linewidth',2), grid subplot(3,2,4),stem(u,Mod_K2, 'markersize',3,'Linewidth',2), grid 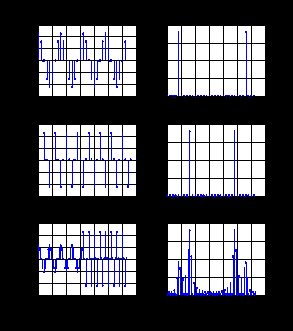  4С. Цифровой единичный импульс на интервале 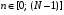 . .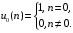 Вывести графики цифрового единичного импульса и модуля его ДПФ. function [ output_args ] = Untitled4( input_args ) N=64; x = [1 zeros(1,(N-1))]; n = 0:(N-1); k = 0:(N-1); % ДИСКРЕТНАЯ НОРМИРОВАННАЯ ЧАСТОТА X = fft(x); % ДПФ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ MOD_K = abs(fft(x)); % МОДУЛЬ ДПФ КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ figure('Name','DFT Modul', 'NumberTitle','off') subplot(2,1,1), stem(n,x,'MarkerSize',3,'Linewidth',2), grid subplot(2,1,2), stem(k,MOD_K,'MarkerSize',3,'Linewidth',2), grid end  5С. Последовательность с однотональной амплитудной модуляцией: 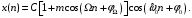 Задать значения 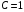 , , 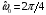 , , 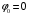 , , 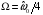 , , 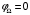 , , 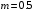 и период последовательности и период последовательности 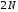 . .Вывести графики последовательности и ее амплитудного спектра. function [ output_args ] = Untitled1( input_args ) N=64; Fs=6000; n = 0:(2*N); k = 0:(2*N); w = (2*pi)/4; x = 1+0.5*cos((w/4)*n).*cos(w*n); % ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ X = fft(x); MOD = (2/N)*abs(X); % АМПЛИТУДНЫЙ СПЕКТР ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ MOD(1) = (1/N)*abs(X(1)); figure('Name','Periodic Sequence','NumberTitle','off') subplot(3,1,1), stem(n,x, 'MarkerSize',3,'Linewidth',2) grid, xlabel('n') ylabel('x(n)'), title(strcat(['Periodic Sequence x(n) N = ',num2str(N)])) subplot(3,1,2), stem(n/Fs,x,'MarkerSize',3,'Linewidth',2) grid, xlabel('nT') ylabel('x(nT)'), title(strcat(['Periodic Sequence x(nT) N = ',num2str(N)])) x = ifft(X); % ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ, ВЫЧИСЛЕННАЯ С ПОМОЩЬЮ ОДПФ subplot(3,1,3), stem(n,x,'MarkerSize',3,'Linewidth',2) grid, xlabel('n') ylabel('x(n)'), title(strcat(['Periodic Sequence x = ifft(X) N = ',num2str(N)])) figure('Name','Amplitude Spectrum','NumberTitle', 'off') subplot(2,1,1), stem(k,MOD,'MarkerSize',3,'Linewidth',2), grid xlabel('k'), ylabel('1/N|X(k)|') title(strcat(['Amplitude Spectrum of the Periodic Sequence N = ',num2str(N)])) subplot(2,1,2), stem(k*(Fs/N),MOD,'MarkerSize',3,'Linewidth',2),grid xlabel('f (Hz)'), ylabel('1/N|X(f)|') title(strcat(['Amplitude Spectrum of the Periodic Sequence N = ',num2str(N)])) end 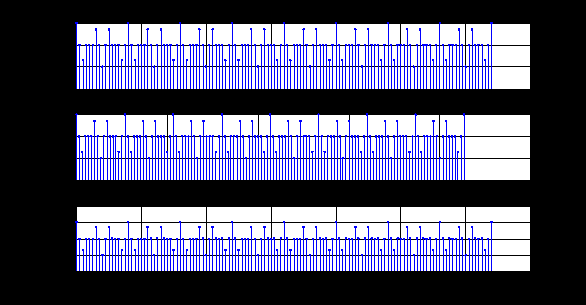 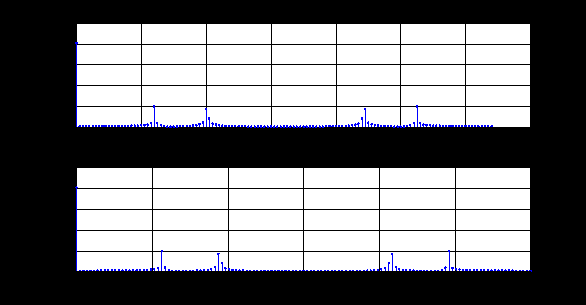 6С. Последовательность 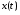 : :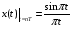 Задать частоту дискретизации 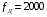 Гц. Гц.Вывести графики последовательности на интервале 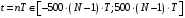 с шагом с шагом 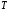 и модуля её ДПФ. и модуля её ДПФ.function [ output_args ] = Untitled1( input_args ) Fs=2000; N=64; K=-15:1/Fs:15; T=1/Fs; n=(-500*(N-1)*T):T: (500*(N-1)*T); f=sin(pi.*n); x=f./(pi.*n); Mod_K=abs(fft(x)); subplot(2,1,1) ,stem(n,x, 'markersize',2,'Linewidth',2), grid subplot(2,1,2),stem(n,Mod_K, 'markersize',2,'Linewidth',2), grid end. Fs=2000; N=64; T=1/Fs; n=(-500*(N-1)*T):T: (500*(N-1)*T); k=-500*(N-1):1: 500*(N-1); f=sin(pi.*n); x=f./(pi.*n); y=fft(x); Mod_K=abs(y); subplot(2,1,1) ,stem(n,x, 'markersize',2,'Linewidth',2), grid subplot(2,1,2),stem(k,Mod_K, 'markersize',2,'Linewidth',2), grid 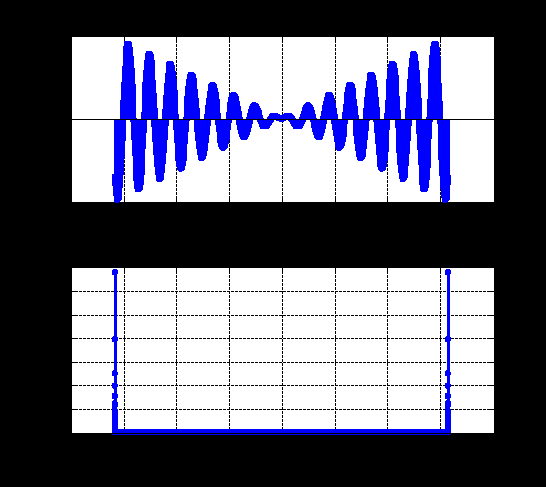 7C. Гауссов радиоимпульс: 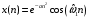 . .Задать 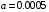 и и 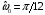 . .Вывести графики последовательности на интервале 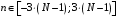 и модуля ее ДПФ. и модуля ее ДПФ.function [ output_args ] = Untitled1( input_args ) N=64; n=(-3*(N-1)):(3*(N-1)); a=0.0005; w0=pi/12; f1=750; Fs=6000; w1 = 2*pi*f1/Fs; x=exp(-a.*n.^2).*cos(w1.*n); Mod_K=abs(fft(x)); subplot(2,1,1) ,stem(n,x, 'markersize',2,'Linewidth',2), grid subplot(2,1,2),stem(n,Mod_K, 'markersize',3,'Linewidth',2), grid end. 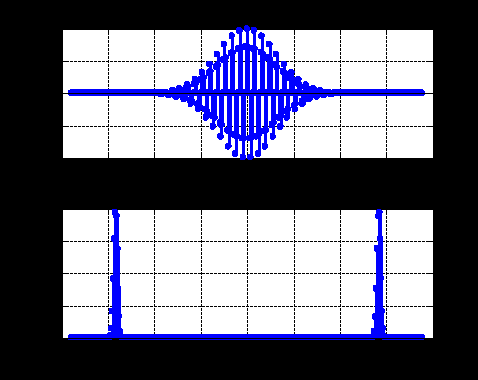 ВЫПОЛНЕНИЕ РАБОТЫ Вариант 12. 1. Вычисление амплитудного и фазового спектров периодической последовательности 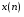 (идентификатор x) с периодом (идентификатор x) с периодом 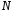 : :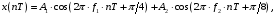 используя её тождественное представление в виде: 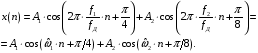 Графики последовательности 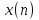 на периоде N в шкале: на периоде N в шкале:
 Амплитудный спектр последовательности 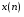 и его гармоники в шкале: и его гармоники в шкале:
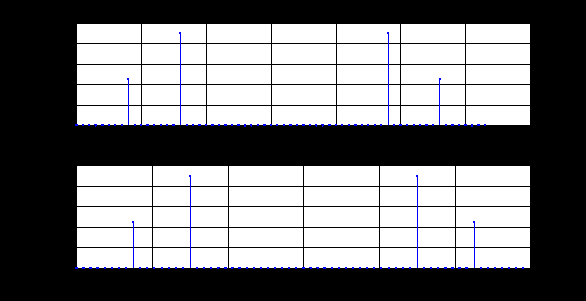 Фазовый спектр последовательности  и его гармоники в шкале: и его гармоники в шкале:
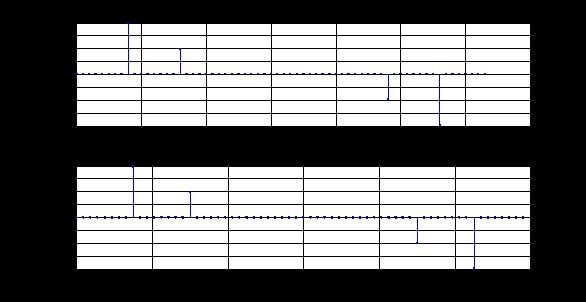 2. Вычисление ДПФ конечной последовательности. Графики в шкале дискретных нормированных частот:
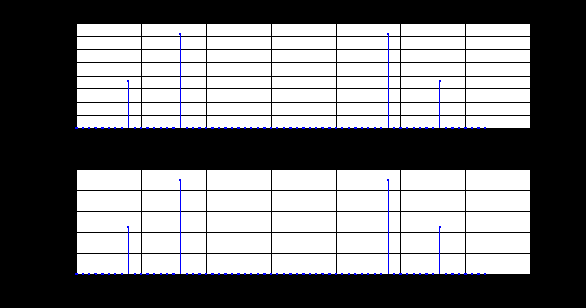 3. Определение амплитуд и частот дискретных гармоник. Выходные параметры function-файла fft_e1: MODm = 1.1200 2.2400 2.2400 1.1200 m = 8 16 48 56 Значения амплитуд, дискретных нормированных частот и абсолютных частот гармоник: A1 = 1.12 A2 = 2.24 k1 = 8 k2 = 16 f1 = 750 f2 = 1500 4. Граничные значения порогов для первого и второго критериев выделения полезного сигнала. Для аддитивной смеси  граничное значение порога: граничное значение порога:
e1_low = 0.27847 e1_up = 1
e2_low = 1.4591 e2_up = 18.8165 5. Выделение полезного сигнала по первому критерию. График аддитивной смеси 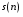 на периоде на периоде 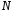 : :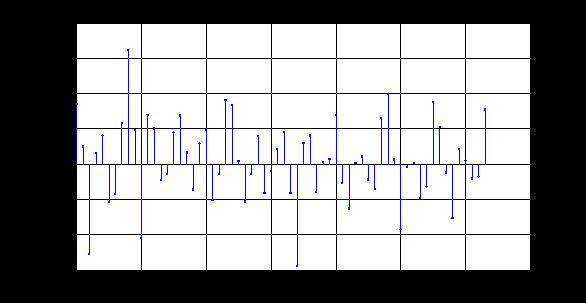 График амплитудного спектра аддитивной смеси 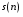 в шкале дискретных нормированных частот и график амплитудного спектра аддитивной смеси в шкале дискретных нормированных частот и график амплитудного спектра аддитивной смеси 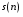 , нормированного к его максимальному значению): , нормированного к его максимальному значению):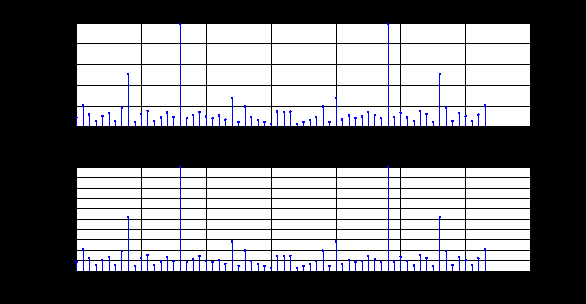 Значение e1: e1 = 0.27847 Выходные параметры function-файла fft_e1. MODm = 1.2696 2.4650 2.4650 1.2696 m = 8 16 48 56 6. Выделение полезного сигнала по второму критерию. График амплитудного спектра аддитивной смеси  Error: Reference source not found в шкале дискретных нормированных частот и график квадрата амплитудного спектра аддитивной смеси Error: Reference source not found в шкале дискретных нормированных частот и график квадрата амплитудного спектра аддитивной смеси  , нормированного к ее средней мощности: , нормированного к ее средней мощности: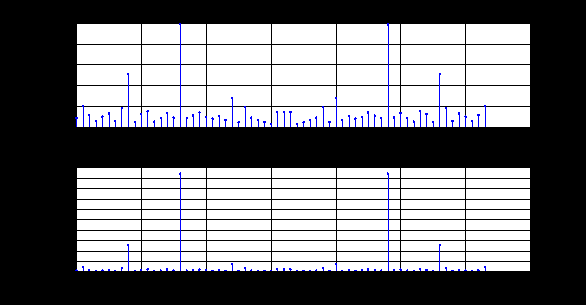 Значение e2: e2 = 1.4591 Выходные параметры function-файла fft_e2. MODm = 1.2696 2.4650 0.6864 0.6864 2.4650 1.2696 m = 8 16 24 40 48 56 7. Восстановление аналогового сигнала. Восстановить периодический аналоговый сигнал  (идентификатор ха) по отсчетам ДПФ (идентификатор ха) по отсчетам ДПФ  периодической последовательности периодической последовательности  Error: Reference source not found. Для вычисления значений сигнала Error: Reference source not found. Для вычисления значений сигнала 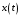 использовать формулу Error: Reference source not found, задавая значением времени t (идентификатор t) на интервале использовать формулу Error: Reference source not found, задавая значением времени t (идентификатор t) на интервале 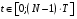 с шагом с шагом 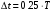 . .В тех же точках вычислить значения исходного аналогового сигнала 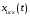 (идентификатор xt), на основе которого получена последовательность (идентификатор xt), на основе которого получена последовательность 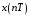 Error: Reference source not found. Error: Reference source not found.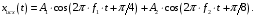 Графики периодической последовательности 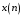 Error: Reference source not found и модуля ее ДПФ; восстановленного аналогового сигнала Error: Reference source not found и модуля ее ДПФ; восстановленного аналогового сигнала 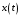 и его амплитудного спектра (идентификатор MODa); исходного аналогового сигнала и его амплитудного спектра (идентификатор MODa); исходного аналогового сигнала 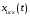 . .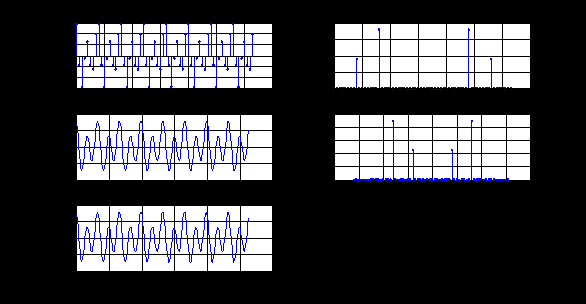 8. Восстановление спектральной плотности конечной последовательности. Вычислить значения спектральной плотности конечной последовательности 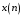 Error: Reference source not found длины Error: Reference source not found длины 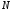 в в 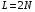 точках на периоде точках на периоде 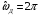 двумя способами: двумя способами:по формуле Error: Reference source not found – идентификатор xw; по формуле Error: Reference source not found – идентификатор xz. Вывести графики модуля ДПФ конечной последовательности 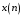 в шкале дискретных нормированных частот с помощью функции stem; модулей спектральной плотности, вычисленной первым и вторым способами в шкале частот в шкале дискретных нормированных частот с помощью функции stem; модулей спектральной плотности, вычисленной первым и вторым способами в шкале частот 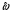 (идентификатор w) с помощью функции plot. (идентификатор w) с помощью функции plot.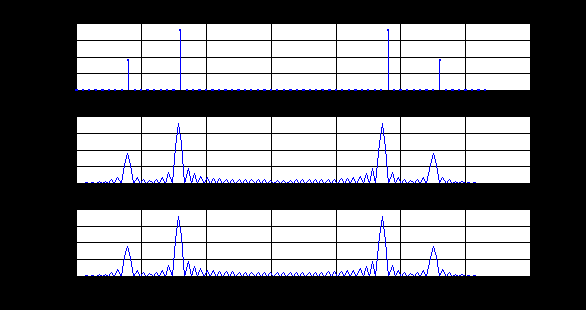 9. Уменьшение периода дискретизации по частоте при вычислении ДПФ. Сформировать три конечные последовательности  Error: Reference source not found (вектор zx) с длинной Error: Reference source not found (вектор zx) с длинной  (вектор L), дополняя их нулями до длины (вектор L), дополняя их нулями до длины 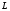 при при 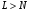 . .Вычислить ДПФ 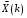 Error: Reference source not found данных последовательностей (вектор xz). Error: Reference source not found данных последовательностей (вектор xz).Графики исходной последовательности и последовательностей, дополненных нулями; их модулей ДПФ в шкале дискретных нормированных частот (пунктиром - помощью функции stem) и одновременно — восстановленных спектральных плотностей (с помощью функции plot красным цветом). 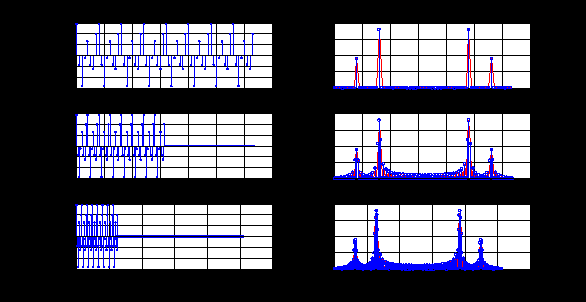 Значения периодов ДПФ (вектор L) и соответствующих им периодов крепитации по частоте (вектор Delta_f). L = [64 128 256] Delta_f = [93.75 46.875 23.4375] |


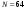
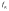


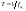
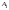
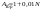
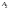
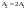
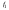
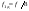
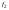
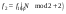
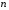 (идентификатор n);
(идентификатор n);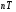 (идентификатор nT).
(идентификатор nT).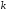 (идентификатор k);
(идентификатор k);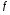 (Гц) (идентификатор f).
(Гц) (идентификатор f).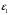 для первого критерия;
для первого критерия;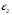 для второго критерия;
для второго критерия;