Спектральный анализ сложных радиотехнических сигналов. Высшая школа электроники и компьютерных наук
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (национальный исследовательский университет)» ВЫСШАЯ ШКОЛА ЭЛЕКТРОНИКИ И КОМПЬЮТЕРНЫХ НАУК Кафедра «Инфокоммуникационные технологии» «Расчёт спектральных характеристик радиотехнических сигналов» ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ по дисциплине «Радиотехнические цепи и сигналы» ЮУрГУ– 110501.2022.008 ПЗ КР
Челябинск 2022 Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (национальный исследовательский университет)» ВЫСШАЯ ШКОЛА ЭЛЕКТРОНИКИ И КОМПЬЮТЕРНЫХ НАУК Кафедра «Инфокоммуникационные технологии»
ЗАДАНИЕ на курсовую работу студента Сидорова Артёма Кирилловича Группа КЭ-310 Дисциплина: «Радиотехнические цепи и сигналы». Тема работы: «Расчёт спектральных характеристик радиотехнических сигналов» Срок сдачи студентом законченной работы: «31» мая 2022 г. Перечень вопросов, подлежащих разработке: Анализ видов сигналов и их характеристик. Характеристики сигналов в частотной области. Свойства преобразования Фурье. Расчеты спектральных характеристик одиночного видеоимпульса и радиоимпульса. Расчеты спектральных характеристик периодической последовательности из видеоимпульсов и периодической последовательности из радиоимпульсов. 6 Календарный план
ОГЛАВЛЕНИЕВВЕДЕНИЕ Теоретические основы радиотехники – это базовая дисциплина в системе профессиональной подготовки специалистов в области радиотехники, радиоэлектроники, радиоинформатики. Ее основной целью является изучение методов и технических средств формирования и обработки радиотехнических сигналов, что необходимо для решения конкретных практических задач в области радиотехники, в частности для создания современных радиотехнических систем, состоящих из большого количества различных устройств. При разработке и исследовании радиотехнических устройств различного уровня сложности и назначения возникают задачи, связанные с анализом и синтезом устройств. В наиболее общем виде данные задачи могут быть сформулированы следующим образом. Задача анализа: заданы радиотехническое устройство, входной сигнал и их основные характеристики; необходимо определить выходной сигнал и его характеристики. Поскольку устройство представляет собой различные комбинации линейных и нелинейных звеньев, то задача по существу сводится к анализу прохождения сигнала через линейные и нелинейные устройства. Требуемый уровень адекватности результатов анализа реальному положению вещей, а также количественные характеристики, подлежащие расчету, определяются тем критерием, по которому оценивается качество работы устройства. Задача синтеза заданы входной сигнал и его основные характеристики, а также выходной сигнал с требуемыми для проектировщика характеристиками; необходимо разработать радиотехническое устройство, которое преобразует входной сигнал с заданными характеристиками в сигнал с желаемыми характеристиками. Частным вариантом задачи синтеза является случай, когда входной сигнал отсутствует и требуется создать устройство для формирования (генерирования) сигнала с желаемыми характеристиками. Основным результатом синтеза являются оптимальные алгоритмы и структурные схемы проектируемого устройства. Синтез устройства не исключает необходимости выполнения некоторых процедур анализа в ходе оценки его работоспособности при возможных отклонениях от принятых априорных данных. При решении задач анализа и синтеза объектами исследования являются сигнал и радиотехническое устройство. Успешное решение этих задач предполагает хорошую ориентацию исследователя и проектировщика во множестве сигналов, способов их аналогового и дискретного представления, методах анализа в частотной и временной областях. Самостоятельное значение имеют вопросы обработки сигналов, включающие в себя методы и технические средства формирования и различных преобразований сигналов. Технические средства – это и есть радиотехнические устройства (цепи), решающие обширный ассортимент задач и характеризуемые многообразием структурной и функциональной организации. Это требует систематизации знаний в области современных методов (уже ставших классическими) физико-математического анализа процессов формирования сигналов, а также их линейных и нелинейных преобразований. Задачей курсовой работы является расчет спектральных характеристик радиотехнических сигналов. Для решения этой задачи необходимо: - рассмотреть и проанализировать виды сигналов; - рассмотреть и проанализировать основные характеристики сигналов в частотной области; - рассмотреть и проанализировать свойства преобразования Фурье; - рассмотреть и проанализировать свойства линейности, сдвига сигнала, спектр производной и интеграла, спектр радиоимпульса. 1 СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ 1.1 Радиотехнические сигналы Сигнал – физический процесс, являющийся функцией некоторых параметров и используемый в качестве носителя информации. В радиотехнике изучают две группы электрических сигналов: детерминированные и случайные. Детерминированные сигналы– это сигналы, мгновенные значения которых в любой момент времени известны, т.е. предсказуемы с вероятностью, равной единице. Они могут быть описаны определенными функциями времени. Анализ и исследование этих сигналов осуществляется с помощью математического аппарата, не связанного с теорией вероятностей. Примером такого сигнала является косинусоидальное колебание, описываемое функцией 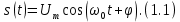 где Um – амплитуда сигнала; ω0 = 2πf0 – угловая частота сигнала; φ – начальная фаза сигнала. Случайные сигналы – это сигналы, мгновенные значения которых в любые моменты времени неизвестны и не могут быть предсказаны с вероятностью, равной единице. Как ни парадоксально на первый взгляд, но сигналом, несущим полезную информацию, может быть только случайный сигнал. Информация в нем заложена во множестве амплитудных, частотных (фазовых) или кодовых изменений передаваемого сигнала. На практике любой радиотехнический сигнал, в котором заложена полезная информация, должен рассматриваться как случайный. Большинство используемых на практике радиотехнических сигналов относится к классу случайных по двум причинам. Во-первых, любой сигнал, являющийся носителем информации, должен рассматриваться как случайный. Во-вторых, в устройствах, которые «работают» с сигналами, практически всегда имеются шумы или помехи, которые накладываются на полезный сигнал. Поэтому в любом канале связи полезный сигнал искажается при передаче и сообщении на приемной стороне воспроизводится с некоторой ошибкой. Непреодолимой границы между детерминированными и случайными сигналами нет. В условиях большого отношения полезного сигнала к шуму, т.е. в случае, когда уровень помех значительно меньше уровня полезного сигнала, детерминированная модель сигнала адекватна реальной ситуации. При этом можно применять методы анализа неслучайных сигналов. 1.2 Математические модели сигналов Для того чтобы сигналы являлись объектами теоретического изучения и анализа, необходимо иметь их математические модели. Математическая модель сигнала – это формализованное его представление в виде определенного математического объекта. Физической величиной, определяющей характер радиотехнического сигнала, обычно является напряжение или ток, изменяющиеся во времени по определенному закону. Поэтому наиболее часто в качестве модели сигнала используется функциональная зависимость, аргументом которой является время, т.е. функция времени. В радиотехнике математической моделью сигнала является функция времени, обозначается s(t), u(t), i(t). Целесообразность использования комплексной формы представления сигнала обусловлена удобством выполнения некоторых математических преобразований. В качестве математической модели сигнала используется также функциональная зависимость, аргументом которой является циклическая f или угловая ω частота, т.е. сигнал рассматривается как функция частоты. Эта функциональная зависимость, являющаяся по существу спектральным представлением сигнала, получила название спектра сигнала. Такое представление сигнала чаще рассматривают не как собственно сигнал, а как характеристику сигнала в частотной области. Сигналы могут быть представлены также в графическом и табличном виде. 1.3 Классификация сигналов Для представления и анализа сигналов приходится применять различные методы, которые зависят от назначения, структуры, математического описания и других свойств сигналов. Поэтому достаточно важным этапом процедуры анализа является классификация радиотехнических сигналов. Классификацию детерминированных сигналов можно производить по различным признакам. Как известно, для передачи информации на расстояние используются модулированные колебания, т.е. высокочастотные колебания, один или несколько параметров которых изменяются по закону передаваемого сообщения. Поэтому в канале связи различают следующие сигналы: - управляющие (модулирующие) сигналы; - высокочастотные (несущие) гармонические колебания; - модулированные колебания (радиосигналы). 1.3.1 Управляющие модулирующие сигналы Управляющие сигналы – это информационные сигналы, подлежащие передаче. Физически они представляют собой электронный вариант какого-либо сообщения, необходимого различным объектам или субъектам. Рассмотрим некоторые виды управляющих сигналов. а. Непрерывные и дискретные сигналы Непрерывные сигналы – это сигналы, имеющие определенное значение в любой момент времени их существования. Возможны точки разрыва в функции, описывающей сигналы этого класса. Такие сигналы называют еще аналоговыми сигналами. Широкое использование в настоящее время дискретных и цифровых систем привело к необходимости применять дискретизированные сигналы. При этом различают сигналы: - дискретные по времени; - квантованные по уровню; -цифровые (дискретные по времени и квантованные по уровню). Указанные классы сигналов представлены на рис. 1.1. 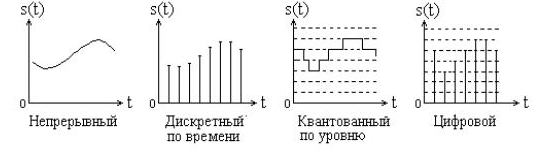 Рисунок 1.1 – Виды управляющих сигналов б. Импульсные сигналы Импульсные сигналы – это сигналы, существующие в пределах конечного отрезка времени. Форма сигналов может быть различной: прямоугольная, треугольная, колоколообразная и др. (рис 1.2, а, б, в). Импульсными сигналами можно считать также сигналы с областью определения (- 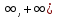 или (0,+ или (0,+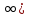 , если существует конечный интервал времени, в пределах которого сосредоточена основная часть их энергии. К числу таких сигналов относят, например, колоколообразные (гауссовы) импульсы, экспоненциальные импульсы и др. (рис 1.2, г, д). , если существует конечный интервал времени, в пределах которого сосредоточена основная часть их энергии. К числу таких сигналов относят, например, колоколообразные (гауссовы) импульсы, экспоненциальные импульсы и др. (рис 1.2, г, д).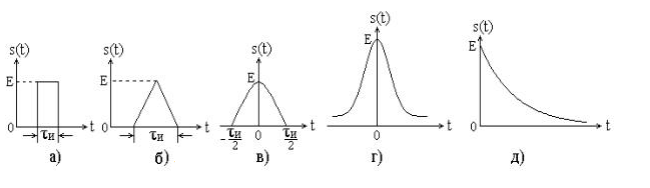 Рисунок 1.2 – Импульсные сигналы в. Периодические и непериодические сигналы Периодические сигналы – это сигналы, которые можно представить функцией времени, удовлетворяющей условию 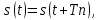 где Т – период сигнала; n= …, -2, -1, 0, 1, 2, …. Непериодические сигналы не удовлетворяют вышеприведенному условию. Обычно в качестве таких сигналов рассматривают одиночные импульсные сигналы, имеющие конечную длительность. Так как признаком периодичности сигнала является его повторяемость, то сигнал конечной длительности можно рассматривать как периодический сигнал с периодом T  . .г. Четные и нечетные сигналы Четные сигналы описываются четной функцией времени, т.е. функцией, удовлетворяющей условию sч(t)=sч(-t). Полярность (знак) такого сигнала не изменяется при изменении знака по оси времени. Следовательно, четный сигнал является симметричным относительно оси ординат (рис. 1.3, а). Нечетные сигналы описываются нечетной функцией времени, т.е. функцией, удовлетворяющей условию sнч(t)=- sнч(-t). Полярность такого сигнала изменяется при изменении знака по оси времени. Нечетный сигнал является симметричным относительно начала координат (рис. 1.3, б). Сигнал, описываемый функцией, не удовлетворяющей условиям четности и нечетности, будем называть произвольным (рис. 1.3, в). 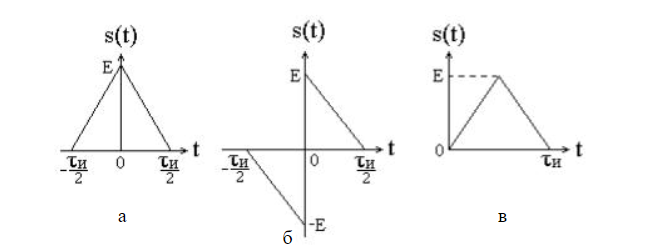 Рисунок 1.3 – Четный(а), нечетный(б) и произвольный(в) сигналы 1.3.2 Испытательные сигналы а. Дельта функция Дельта-функция ( 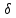 -функция, функция Дирака) – это математическая модель реально не существующего сигнала, который имеет бесконечную по вели-чине амплитуду и нулевую длительность (рис. 1.4). Сигнал, описываемый дельта-функцией, обозначают -функция, функция Дирака) – это математическая модель реально не существующего сигнала, который имеет бесконечную по вели-чине амплитуду и нулевую длительность (рис. 1.4). Сигнал, описываемый дельта-функцией, обозначают 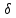 (t) и называют просто -функция. (t) и называют просто -функция.Сигнал называется испытательным, так как он применяется для получения импульсной характеристики радиотехнического устройства. Реакция устройства на дельта-функцию – это и есть его импульсная характеристика. 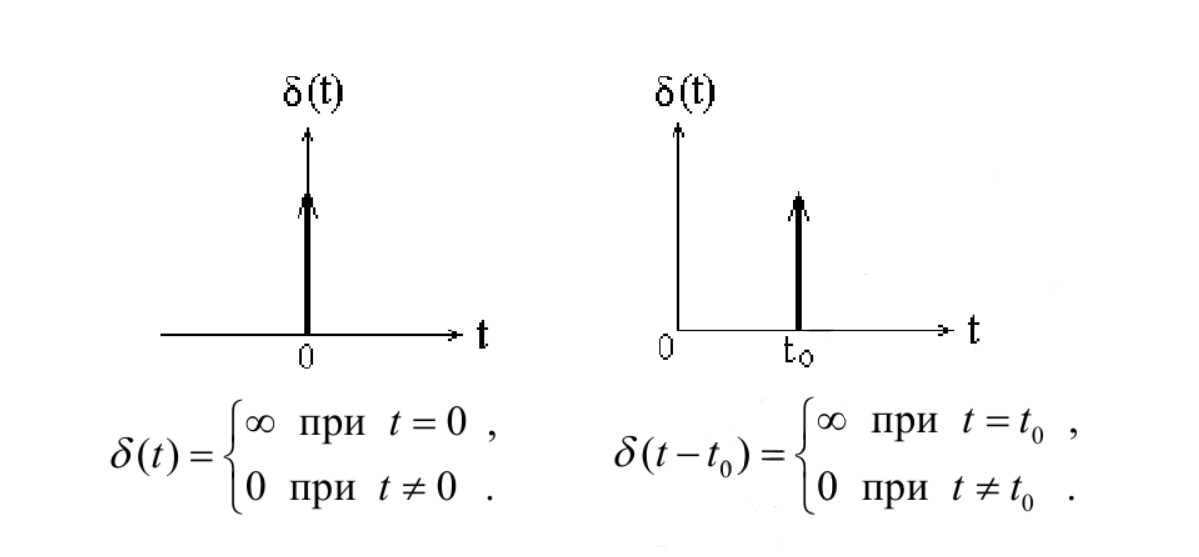 Рисунок 1.4 – Дельта-функция Свойства дельта-функции, благодаря которым она широко используется в математике, физике и радиотехнике: 1) площадь сигнала, описываемого  -функцией, равна 1 т.е. -функцией, равна 1 т.е.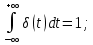 2) селектирующее свойство 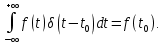 Селектирующее свойство становится понятным, если учесть, что 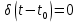 на всей оси времени, кроме точки на всей оси времени, кроме точки 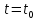 . Это позволяет сделать интервал интегрирования бесконечно малым в окрестности точки t0. В этом интервале функция f(t) принимает значение f(t0), позволяющее ее вынести за знак интеграла. . Это позволяет сделать интервал интегрирования бесконечно малым в окрестности точки t0. В этом интервале функция f(t) принимает значение f(t0), позволяющее ее вынести за знак интеграла.Как следует из свойств колоколообразного импульса и сигнала, описываемого -функцией, справедливо следующее соотношение 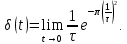 б. Функция единичного скачка Функция единичного скачка (функция Хевисайда) описывает процесс резкого (мгновенного) перехода физического устройства из одного состояния в другое. На рис. 1.5 приведен график этой функции. Сигнал называется испытательным, так как он применяется для получения переходной характеристики радиотехнического устройства. Реакция устройства на единичную функцию – это и есть его переходная характеристика. 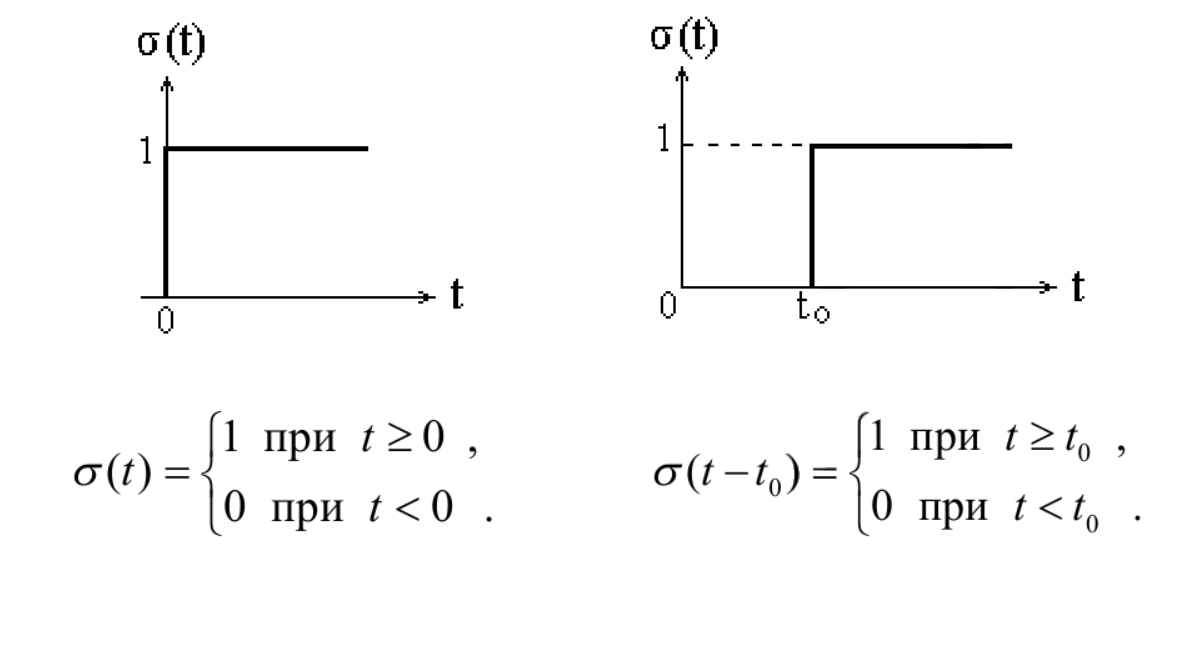 Рисунок 1.5 – Функция единичного скачка Связь между функция 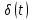 и и 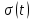 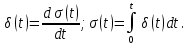 в. Гармонический сигнал Гармонический сигнал также является испытательным сигналом, так как с его помощью определяются частотные характеристики устройств. 1.4 Характеристики сигналов Для сигнала, существующего в интервале 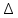 t=t2-t1, наиболее важными являются следующие характеристики (предполагаем, что сигнал представлен в комплексной форме): t=t2-t1, наиболее важными являются следующие характеристики (предполагаем, что сигнал представлен в комплексной форме):Среднее значение сигнала 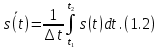 Среднее значение сигнала – это по существу его постоянная составляющая. Мгновенная мощность сигнала 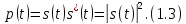 Энергия сигнала 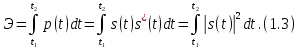 Средняя мощность сигнала 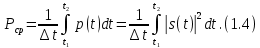 Для периодического сигнала, энергия которого равна бесконечности, среднее значение и энергетические характеристики определяются в пределах одного периода: Среднее значение сигнала 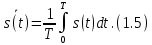 Мгновенная мощность сигнала 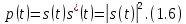 Энергия сигнала 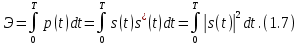 Средняя мощность сигнала 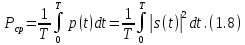 В данном разделе были рассмотрены виды сигналов и их характеристики. 2 ХАРАКТЕРИСТИКИ СИГНАЛОВ В ЧАСТОТНОЙ ОБЛАСТИ Сигналы, используемые в радиотехнике, имеют достаточно сложную структуру. Математическое описание таких сигналов является трудной задачей. Поэтому для упрощения процедуры анализа сигналов и прохождения их через радиотехнические цепи используют прием, предусматривающий разложение сложных сигналов на совокупность идеализированных математических моделей, описываемых элементарными функциями. Гармонический спектральных анализ периодических сигналов предполагает разложение в ряд Фурье по тригонометрическим функциям – синусам и косинусам. Эти функции описывают гармонические колебания, которые сохраняют свою форму в процессе преобразования линейными устройствами (изменяются только амплитуда и фазы), что позволяет использовать теорию колебательных систем для анализа свойств радиотехнических цепей. Ряд Фурье можно представить в виде 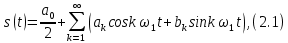 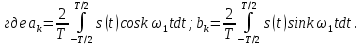 Практическое применение имеет другая форма записи ряда Фурье 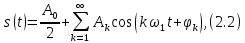 где 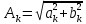 – амплитудный спектр; – амплитудный спектр; 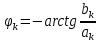 – фазовый спектр. – фазовый спектр.Комплексная форма ряда Фурье 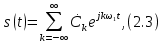 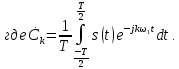 Представленные выше формулы используются для получение спектральной характеристики периодического сигнала. Для получения спектра непериодического сигнала используются преобразования Фурье. Прямое преобразование Фурье 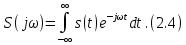 Обратное преобразование Фурье 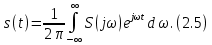 Выражения (2.4), (2.5) являются основными соотношениями для получения спектральных характеристик. 3 СВОЙСТВА ПРЕОБРАЗОВАНИЙ ФУРЬЕ Формулы прямого и обратного преобразования Фурье позволяют по сигналу s(t) определить его спектральную плотность S(jω) и, если в этом есть необходимость, по известной спектральной плотности S(jω) определить сигнал s(t). Для обозначения этого соответствия между сигналом и его спектром применяется символ s(t)↔ S(jω). С помощью свойств преобразований Фурье можно определить спектр измененного сигнала, преобразуя спектр первоначального сигнала. Основные свойства: Линейность s1(t)↔ S1(jω) ⁞ ⁞ sn(t)↔ Sn(jω) ___________________________ 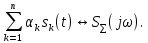 Воспользуемся прямым преобразованием Фурье 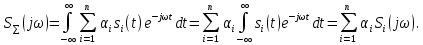 Окончательный результат 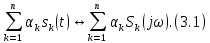 Вывод: прямое преобразование Фурье, является линейной операцией, обладает свойствами однородности и аддитивности. Поэтому спектр суммы сигналов равен сумме спектров. Спектр сигнала, сдвинутого во времени s(t)↔ S(jω) ____________ s(t±t0)↔Sc(jω). 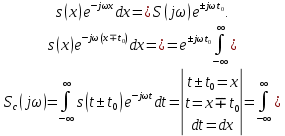 Окончательный результат 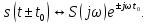 (3.2) (3.2)Вывод: сдвиг сигнала во времени на величину ±t0 приводит к изменению фазовой характеристики спектра на величину ±ωt0. Амплитудный спектр не изменяется. Изменение масштаба во времени s(t)↔ S(jω) ___________________________ s(αt)↔ Sм(jω). 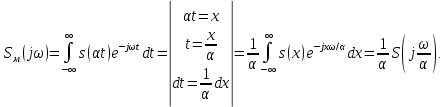 Окончательный результат 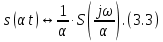 Вывод: при сжатии (расширении) сигнала во времени в определенное число во столько же раз расширяется (сжимается) его спектр по оси частот при пропорциональном уменьшении (увеличении) амплитуд его составляющих. Спектр производной s(t)↔ S(jω) ___________________________ ds(t)/dt↔ Sп(jω). Для определения спектра производной сигнала возьмем производную по времени от правой и левой части обратного преобразования Фурье: 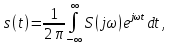 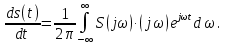 Окончательный результат 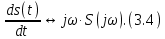 Вывод: спектр производной сигнала равен спектру исходного сигнала, умноженному на jω. При этом амплитудный спектр изменяется пропорционально изменению частоты, а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная π/2 при ω>0 и равная -π/2 при ω<0. Спектр интеграла s(t)↔ S(jω) ___________________________ 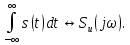 Возьмем интеграл от правой и левой части обратного преобразования Фурье 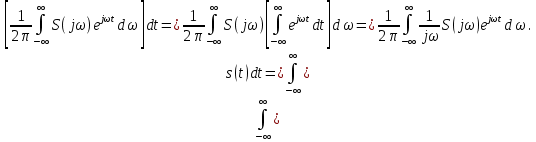 Сравнивая результат с обратным преобразованием Фурье, получаем 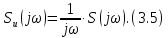 Окончательный результат 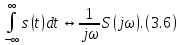 Вывод: спектр сигнала, равного интегралу от исходного сигнала, равен спектру исходного сигнала, деленному на jω. При этом амплитудный спектр изменяется обратно пропорционально изменению частоты, а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная π/2 при ω<0 и равная -π/2 при ω>0. Спектр произведения двух сигналов s1(t)↔ S1(jω) s2(t)↔ S2(jω) ___________________________ s1(t) s2(t)↔ Sпр(jω). Найдем спектр произведения двух сигналов с помощью обратного преобразования Фурье 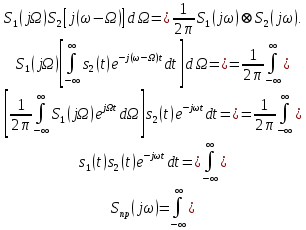 Окончательный результат 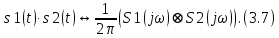 Вывод: Спектр произведения двух сигналов равен свертке их спектров, умноженной на коэффициент 1/(2π). 7. Свойство дуальности Если сигналу s(t) соответствует амплитудный спектр S(ω), то сигналу, имеющему форму такую же, как форма амплитудного спектра S(ω), соответствует спектр, имеющий форму сигнала s(t). 8. Смещение спектра сигнала sв(t)↔ Sв(jω) ___________________________ sр(t)=sв(t)cos(ω0t)↔Sр(jω). Произведение двух сигналов s1(t) и s2(t)= cos(ω0t+ φ) образует гармонический сигнал s(t)= s1(t)cos(ω0t+ φ). Так если s1(t) – видеоимпульс, то s(t) – это радиоимпульс с несущей частотой ω0. Определим спектральную плотность сигнала s(t): 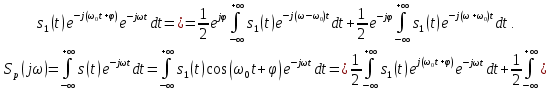 Таким образом, спектральная плотность сигнала sр(t) равна 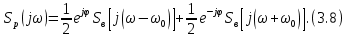 Вывод: При умножении сигнала на гармоническую функцию образуется сигнал, спектр которого представляет собой преобразованный спектр сигнала s1(t). Суть преобразования заключается в переносе спектра на ±ω0 с уменьшением вдвое его величины. Рассмотренные свойства преобразования Фурье значительно облегчают вычисление спектров различных сигналов. 4 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ОДИНОЧНОГО ВИДЕОИМПУЛЬСА Из условия нам известно: Е = 8 В; τи = 8 мкс, где Е – амплитуда импульса, 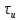 – длительность импульса. – длительность импульса.В соответствии с заданием курсовой работы, необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 4.1. 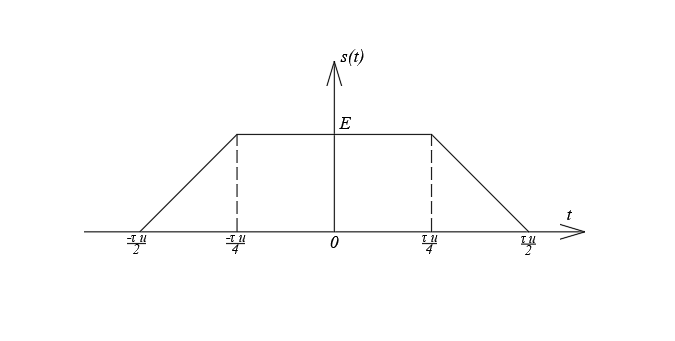 Рисунок 4.1- Одиночный видеоимпульс Как видно из рисунка 4.1, сигнал является одиночным видеоимпульсом, т.е. непериодическим сигналом. Для определения спектра этого сигнала используем прямое преобразование Фурье. Как видно из формулы (2.4), для расчета спектра сигнала необходимо знать формулу этого сигнала. Найдем сигнал пользуясь рисунком 1. Как видно из графика, сигнал можно описать формулой 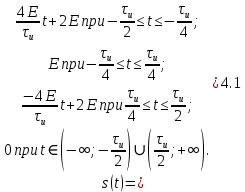 Подставим формулу сигнала в прямое преобразование Фурье 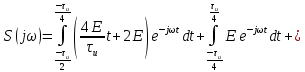 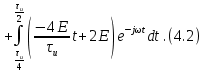 Вычислив интегралы и преобразуя полученные выражения получим 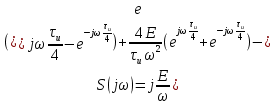 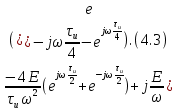 Для того, чтобы отделить мнимую часть от действительной воспользуемся формулами Эйлера, которые представлены ниже 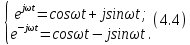 Применив эти формулы к полученной формуле, мы имеем 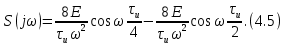 Спектральная плотность представлена в виде выражения 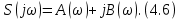 Действительная часть спектра 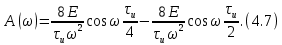 Мнимая часть спектра 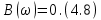 Амплитудный спектр видеоимпульса 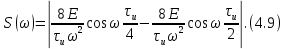 Фазовый спектр видеоимпульса 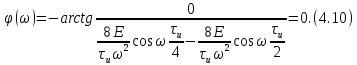 Амплитудный спектр видеоимпульса с числовыми значениями: 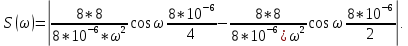 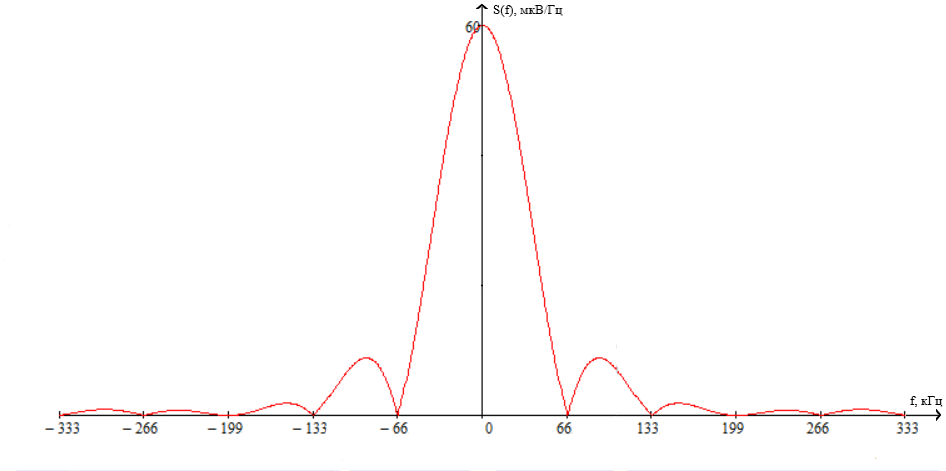 Рисунок 4.2-Амплитудный спектр видеоимпульса Как видно из рисунка 4.2, данный видеоимпульс является низкочастотным гармоническим колебанием 5 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ОДИНОЧНОГО РАДИОИМПУЛЬСА Из условия нам известно: Е = 8 В; τи = 8 мкс; f0=20 МГц, где Е – амплитуда импульса, 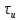 – длительность импульса, f0 – циклическая частота. – длительность импульса, f0 – циклическая частота.В соответствии с заданием курсовой работы, необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 5.1. 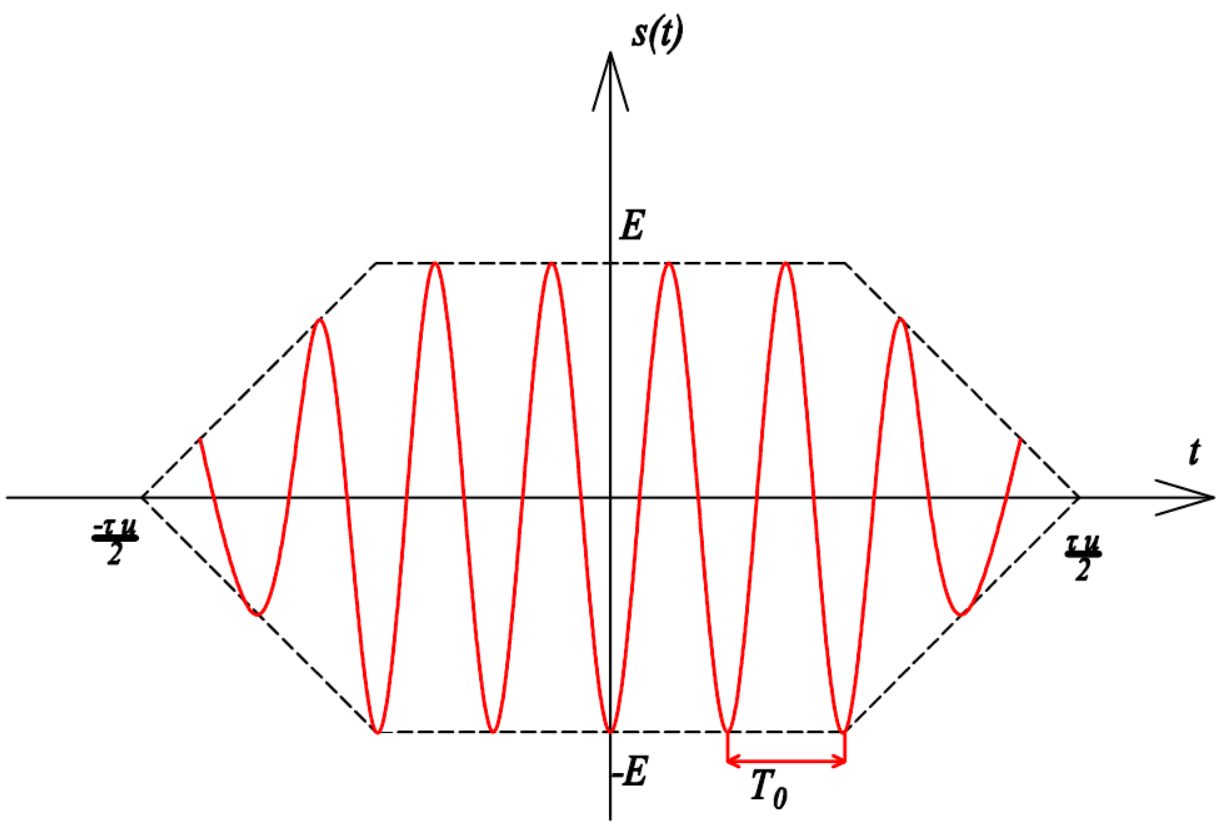 Рисунок 5.1- Одиночный радиоимпульс Как видно из рисунка 5.1, сигнал является одиночным радиоимпульсом, т.е. непериодическим сигналом. Для определения спектра этого сигнала используем одно из свойств преобразований Фурье, а именно смещением спектра сигнала. Подставим формулу (4.5) спектра видеоимпульса в формулу (3.8) свойства смещения спектра сигнала 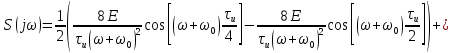 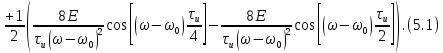 После преобразования получим 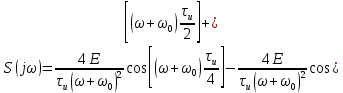 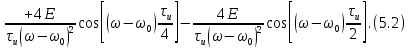 Действительная часть спектра 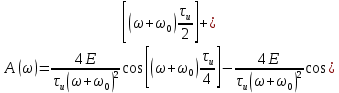 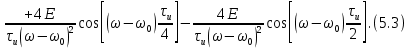 Мнимая часть спектра 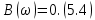 Амплитудный спектр радиоимпульса 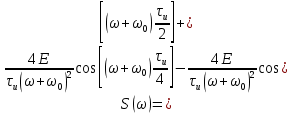 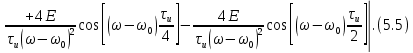 Фазовый спектр видеоимпульса 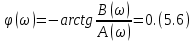 Для подстановки числовых значений в формулу амплитудного спектра радиоимпульса необходимо вычислить угловую частоту 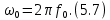 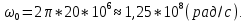 Амплитудный спектр радиоимпульса с числовыми значениями 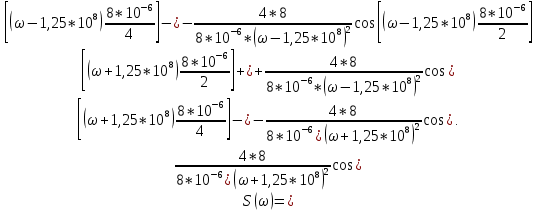 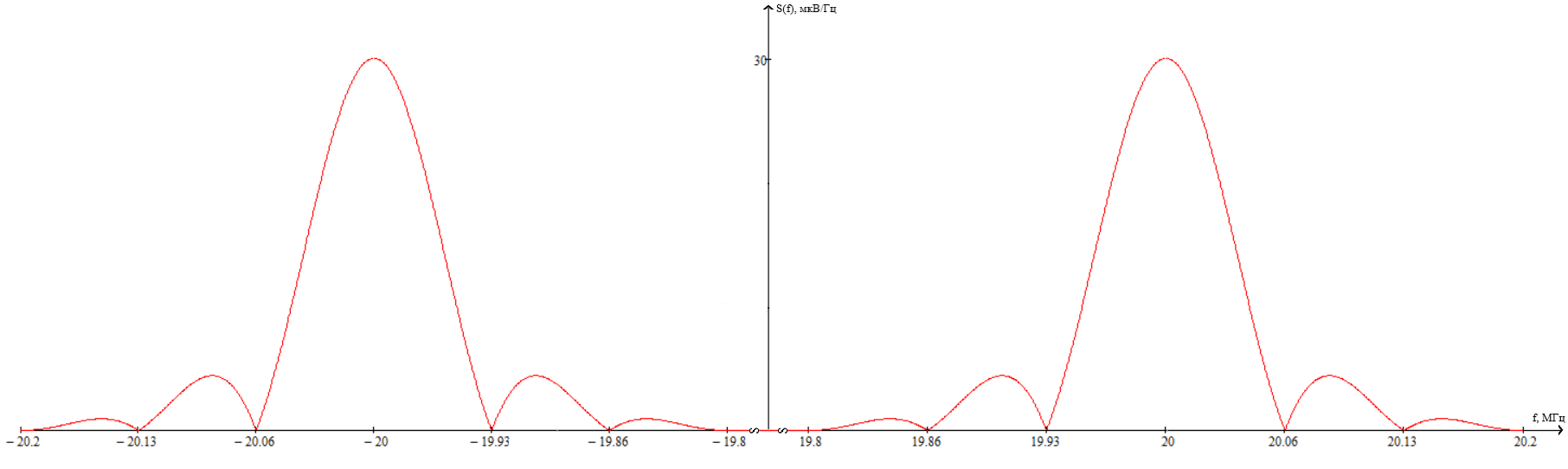 Рисунок 5.2-Амплитудный спектр радиоимпульса Как видно из рисунка 5.2, данный радиоимпульс является высокочастотным гармоническим колебанием. 6 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ВИДЕОИМПУЛЬСОВ Из условия нам известно: Е = 8 В; τи = 8 мкс; Т=500 мкс, где Е – амплитуда импульса, 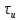 – длительность импульса, Т – период. – длительность импульса, Т – период.В соответствии с заданием курсовой работы, необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 6.1. 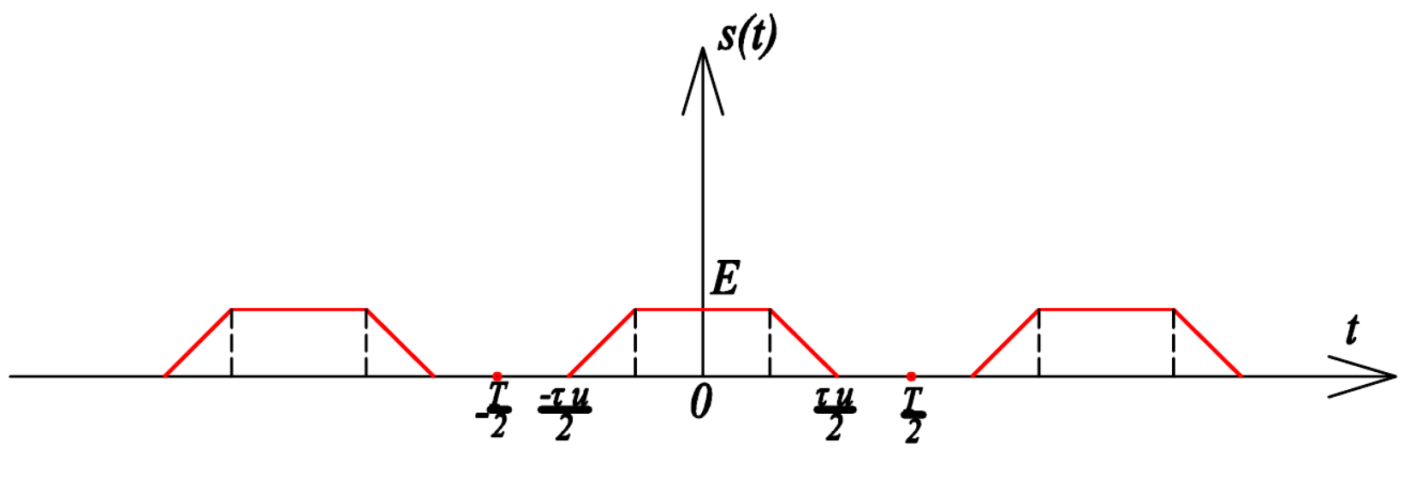 Рисунок 6.1- Периодическая последовательность видеоимпульсов Как видно из рисунка 6.1, сигнал является периодической последовательностью видеоимпульсов. Зная спектр одиночного видеоимпульса, легко определить спектр периодической последовательности видеоимпульсов, используя связь между ними 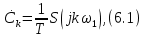 где 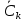 – амплитуда сигнала, – амплитуда сигнала, 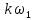 – частота сигнала(k=1, 2, 3, …). – частота сигнала(k=1, 2, 3, …).Найдем значение 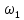 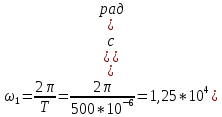 Подставив формулу (4.5) спектра одиночного видеоимпульса в формулу (6.1) 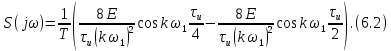 Действительная часть спектра 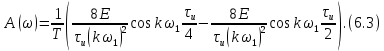 Мнимая часть спектра 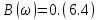 Амплитудный спектр периодической последовательности видеоимпульсов 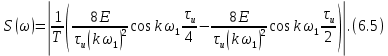 Фазовый спектр периодической последовательности видеоимпульсов 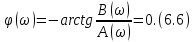 Амплитудный спектр периодической последовательности видеоимпульсов с числовыми значениями 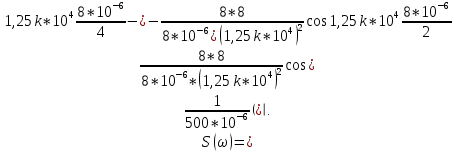 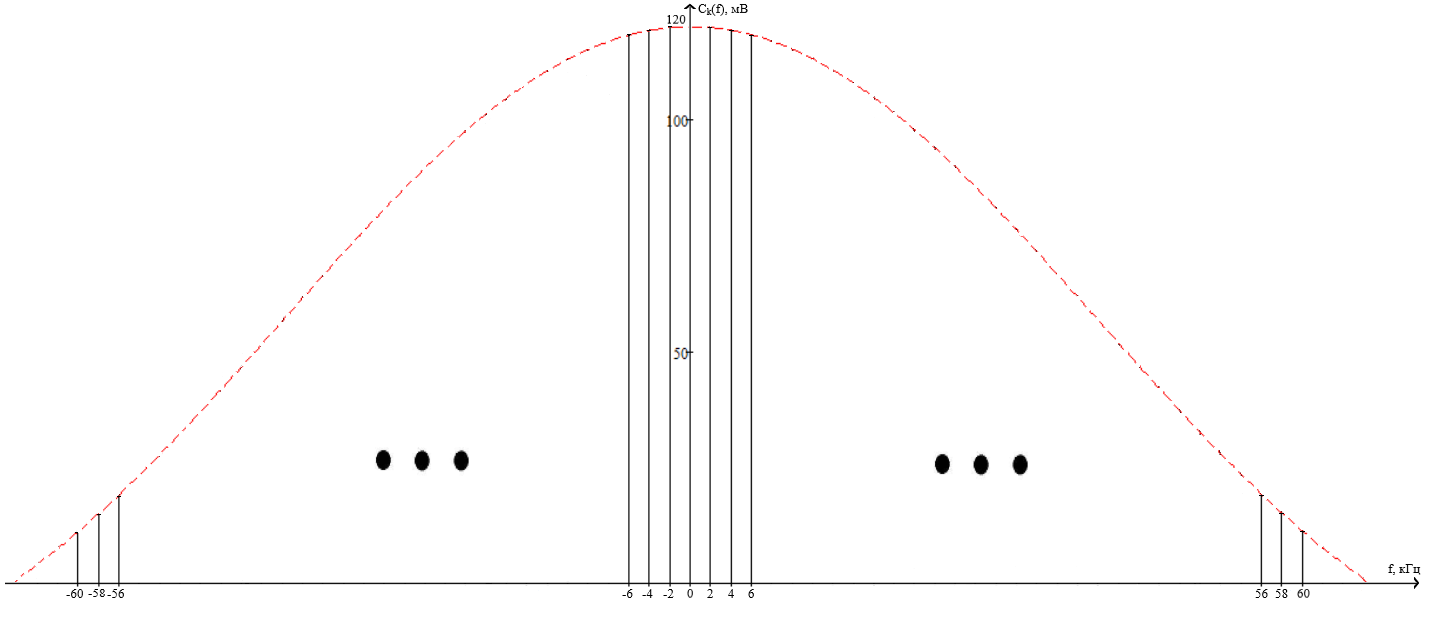 Рисунок 6.2-Амплитудный спектр периодической последовательности видеоимпульсов Как видно из рисунка 6.2, данная последовательность видеоимпульсов является низкочастотными гармоническими колебаниями. 7 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ РАДИОИМПУЛЬСОВ Е = 8 В; τи = 8 мкс; f0=20 МГц; Т=500 мкс, где Е – амплитуда импульса, 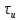 – длительность импульса, f0 – циклическая частота, Т – период. – длительность импульса, f0 – циклическая частота, Т – период.В соответствии с заданием курсовой работы, необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 7.1. 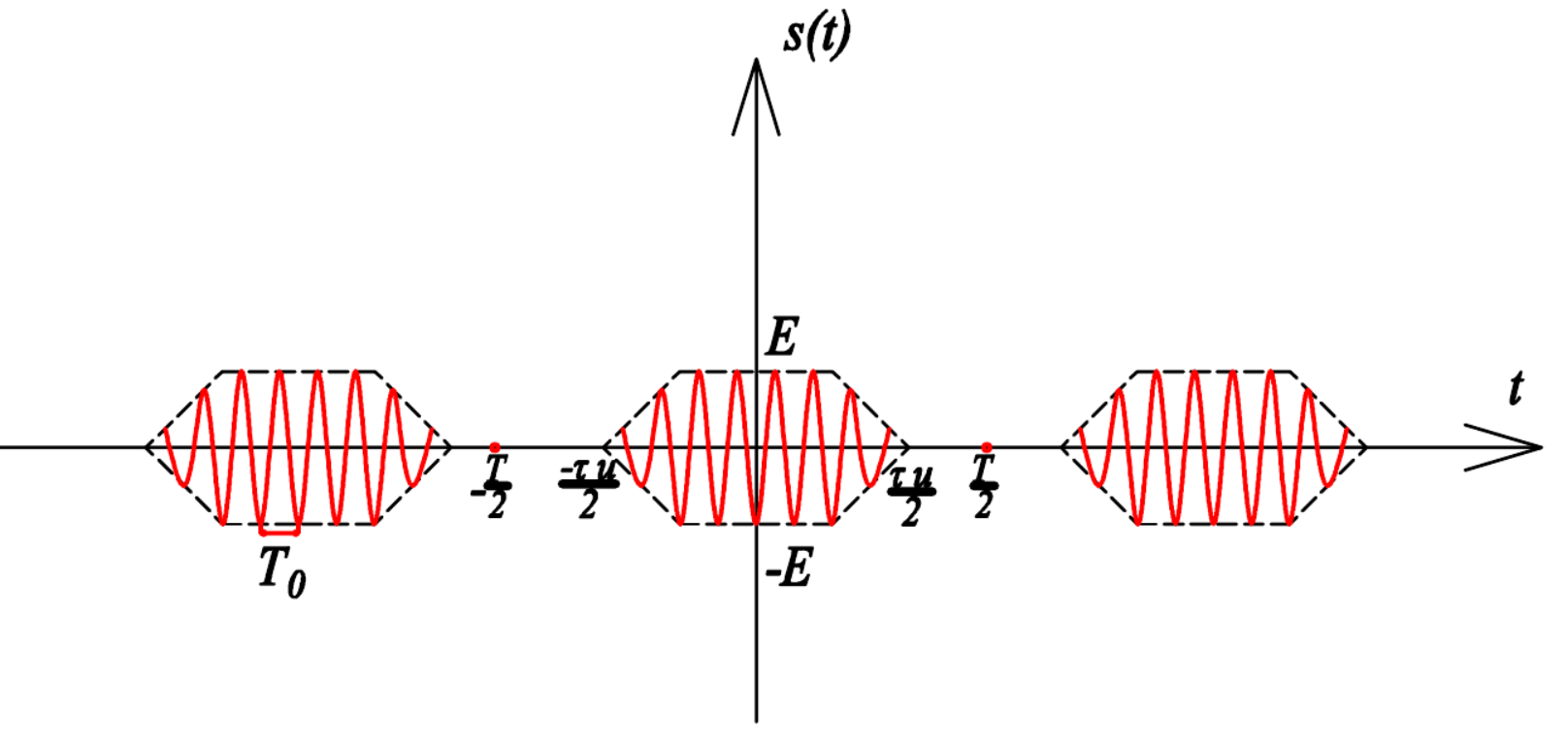 Рисунок 7.1- Периодическая последовательность радиоимпульсов Как видно из рисунка 6.1, сигнал является периодической последовательностью радиоимпульсов. Зная спектр одиночного радиоимпульса, легко определить спектр периодической последовательности радиоимпульсов, используя связь между ними. Подставив формулу (5.2) спектра одиночного радиоимпульса в формулу (6.1) 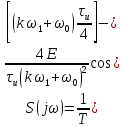 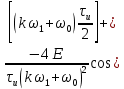 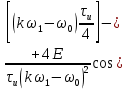 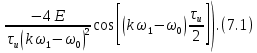 Действительная часть спектра 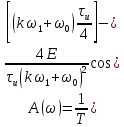 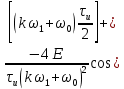 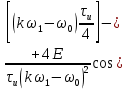 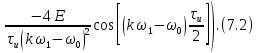 Мнимая часть спектра 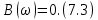 Амплитудный спектр периодической последовательности радиоимпульсов 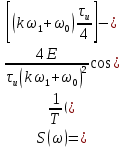 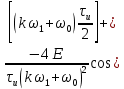 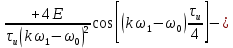 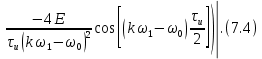 Фазовый спектр периодической последовательности радиоимпульсов 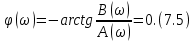 Амплитудный спектр периодической последовательности радиоимпульсов с числовыми значениями 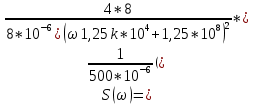 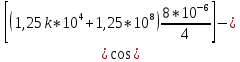 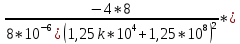 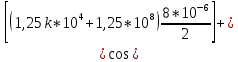 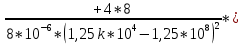 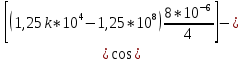 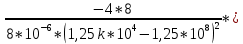 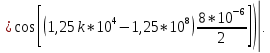 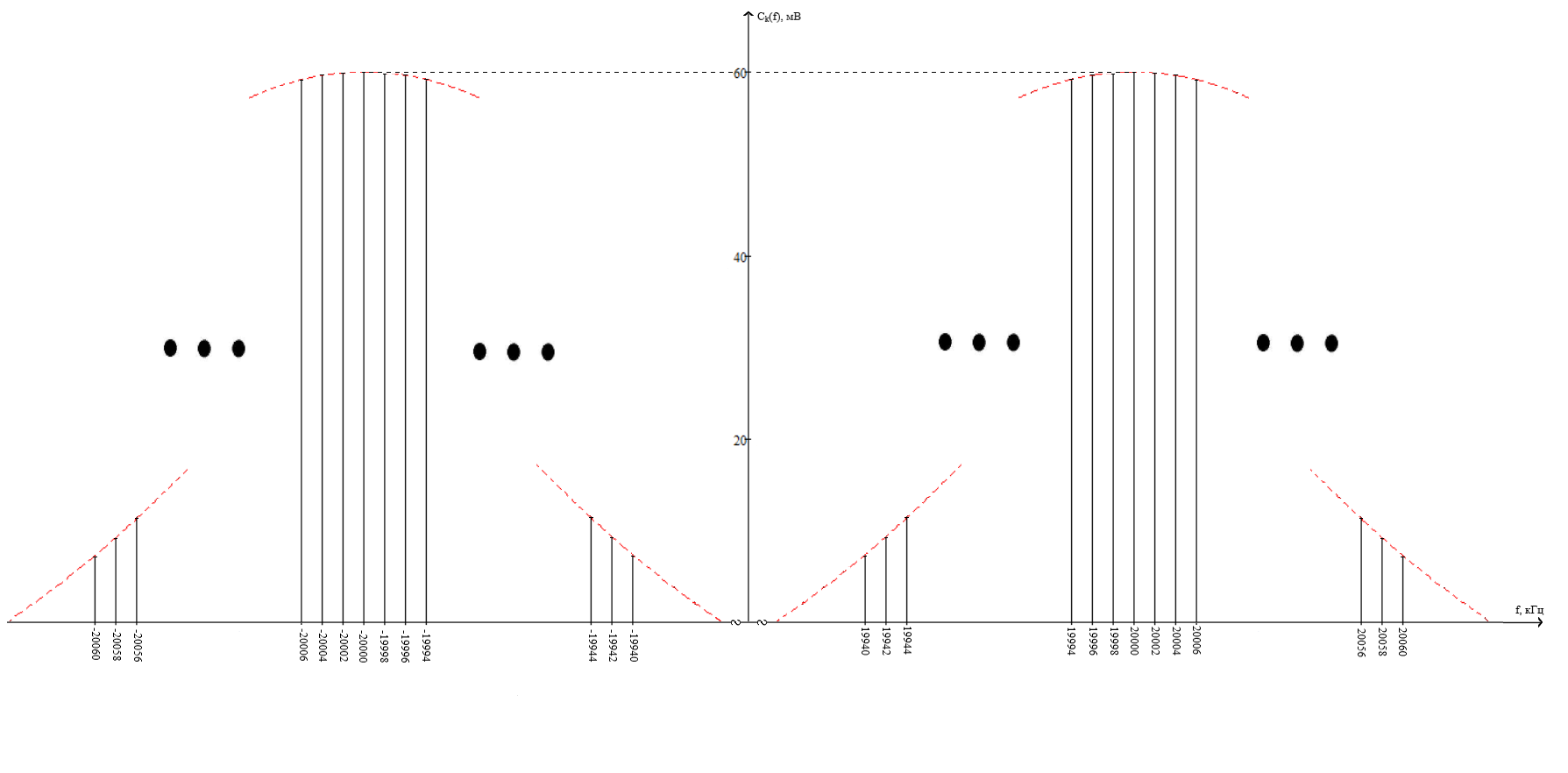 Рисунок 7.2-Амплитудный спектр периодической последовательности радиоимпульсов Как видно из рисунка 7.2, данная последовательность радиоимпульсов является высокочастотными гармоническими колебаниями. ЗАКЛЮЧЕНИЕ Во время выполнения курсовой работы, был произведен расчет амплитудного и фазового спектров одиночных видео- и радиоимпульсов, и периодических последовательностей видео- и радиоимпульсов. В ходе решения данной задачи был определен спектр одиночного видеоимпульса при помощи прямого преобразования Фурье. При помощи свойств преобразования Фурье также были рассчитаны спектры других сигналов. В ходе выполнения курсовой работы убедились в том, что свойства преобразований Фурье упрощают расчёт спектров непериодических сигналов. Данная работа подтверждает, что спектр периодического сигнала дискретен, а непериодического сигнала сплошной. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
