Реферат на тему ЛИФ системы. Системы и лив системы

• Название: Системы и лив системы
• Анкор: Реферат на тему ЛИФ системы
• Дата: 05.05.2022
• Размер: 382.74 Kb.
• Имя файла: Referat_liv_sistemy.docx
• Тип: Реферат; #514068

Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего образования

«Пермский национальный исследовательский политехнический университет»

Кафедра «Ракетно-космическая техника и энергетические системы»

Реферат

На тему «Системы и ЛИВ системы»

Выполнил: студент группы ГПУД-17бз

Духанин В.К.

Проверил: ст. пр.

Матюнин О.О.

Пермь, 2022 г.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 2

1 ЛИВ СИСТЕМЫ 4

1.1Линейные инвариантные во времени системы 4

1.2 Применение интеграла свертки для анализа реакции ЛИВ-систем на входной сигнал 12

1.3 Передаточная функция 15

Заключение 17

Список литературы 20

Приложение 1 21

ВВЕДЕНИЕ

Интеграл свертки является наиболее общим представлением ЛИВ- систем и непрерывного времени. Применение интеграла свертки для расчета реакции системы, по существу, является методом ее анализа во временной области, в то время как применение преобразования Лапласа – методом анализа в частотной области. Выбор метода для анализа зависит от ряда причин. К примеру, если известна весовая функция системы, то проще сразу же воспользоваться интегралом свертки. Если же известна передаточная функция – то проще применить обратное преобразование Лапласа. Чтобы проиллюстрировать применение интеграла свертки для исследования реакции системы на входной сигнал, рассмотрим в начале реакцию линейной системы на синусоидальный входной сигнал.

Объект исследования: Теория цифровой обработки сигналов

Предмет исследования: ЛИВ СИСТЕМЫ

Целью работы является анализ специализированной литературы о ЛИВ системах

Для выполнения цели, были определены задачи:

1. 
   Изучить теоретические аспекты по данной теме;
   
2. 
   Представить передаточную функцию;
   
3. 
   Сделать вывод о функциональном значении ЛИВ систем
   

Метод исследования: анализ литературных источников.

1 ЛИВ СИСТЕМЫ

1. Линейные инвариантные во времени системы

Системы, которые могут быть описаны линейными дифференциальными

уравнениями с постоянными коэффициентами, носят название линейных

инвариантных во времени систем ( ЛИВ–систем). Для таких систем сигнал

на выходе g(t), соответствующий импульсу бесконечно малой

продолжительности на входе, называется импульсной характеристикой

системы. Используются также следующие названия: весовая функция,

импульсная переходная характеристика, функция импульcной реакции и

др. Весовая функция g(t) полностью характеризует поведение ЛИВ-

системы. В одномерных физических системах, в которых независимой

переменной является время, весовая функция g(t) должна быть равна нулю

для отрицательных значений t. Такие системы называют физически

реализуемыми (или удовлетворяющие принципу причинности). В таких

системах реакцию на входное воздействие можно наблюдать только после

подачи на ее вход какого–либо воздействия. В этой связи системы,

удовлетворяющие принципу причинности, называют еще казуальными.

Линейные инвариантные во времени системы характеризуются

следующими свойствами

В Системный анализ, среди других областей исследования, линейная инвариантная во времени система (или «система LTI») - это система, которая производит выходной сигнал из любого входного сигнала с учетом ограничений линейность и временная инвариантность; эти термины кратко определены ниже.

Эти свойства применимы (точно или приблизительно) ко многим важным физическим системам, и в этом случае отклик у (т) системы на произвольный вход х (т) можно найти напрямую, используя свертка: у (т) = х (т) * ч (т) куда ч (т) называется системным импульсивный ответ и представляет свертку (не путать с умножением, как часто используется символ в компьютерные языки).

Более того, существуют систематические методы решения любой такой системы (определение ч (т)), тогда как системы, не отвечающие обоим свойствам, обычно труднее (или невозможно) решить аналитически.

Хорошим примером системы LTI является любая электрическая цепь, состоящая из резисторов, конденсаторов, катушек индуктивности и линейных усилителей.

Теория линейных инвариантных во времени систем также используется в обработка изображений, где системы имеют пространственные измерения вместо временного измерения или в дополнение к нему.

Эти системы могут называться линейный трансляционно-инвариантный чтобы дать терминологию наиболее общий охват. В случае общего дискретное время (т.е. отобранный) системы, линейный инвариантный к сдвигу - соответствующий член.

Теория систем LTI - это область Прикладная математика, который имеет прямое применение в анализ и проектирование электрических цепей, обработка сигналов и конструкция фильтра, теория управления, машиностроение, обработка изображений, дизайн измерительные приборы многих видов, ЯМР-спектроскопия, и многие другие технические области, где системы обыкновенные дифференциальные уравнения представить себя.

Системы, которые могут быть описаны линейными дифференциальным уравнениями с постоянными коэффициентами, носят название линейных инвариантных во времени систем (ЛИВ–систем).

Для таких систем сигнала выходе g(t), соответствующий импульсу бесконечно малой продолжительности на входе, называется импульсной характеристикой системы. Используются также следующие названия: весовая функция, импульсная переходная характеристика, функция импульсной реакции и др.

Весовая функция g(t) полностью характеризует поведение ЛИВ-системы. В одномерных физических системах, в которых независимой переменной является время, весовая функция g(t) должна быть равна нулю для отрицательных значений t. Такие системы называют физически реализуемыми (или удовлетворяющие принципу причинности).

В таких системах реакцию на входное воздействие можно наблюдать только после подачи на ее вход какого–либо воздействия. В этой связи системы, удовлетворяющие принципу причинности, называют еще казуальными. Линейные инвариантные во времени системы характеризуются следующими свойствами:

Свойство линейности: если x1(t) и x2 (t) – два входных сигнала, а y1 (t) иy2 (t) – соответствующие им выходные сигналы, то линейная комбинация η1x1(t) + η2x2 (t) входных сигналов дает на выходе туже самую линейную комбинацию выходных сигналов η1y1 (t) и η2y2(t).

Свойство неизменности (инвариантности) во времени: если входной сигнал x(t) задержать на время г, так что x(t)= x(t-г), то выходной сигнал y(t) задержится на тоже самое время и будет иметь туже самую форму y(t-г) и тем же самым смещением.

Это свойство обеспечивается тем, что весовая функция системы g(t) не зависит от времени (система не стареет во времени).

1.2 Применение интеграла свертки для анализа реакции ЛИВ-систем на входной сигнал

Для физически реализуемых ЛИВ- систем, для которых весовая функция g(t) = 0 при t < 0, реакцию y(t) на произвольный входной сигнал x(t) можно найти, воспользовавшись интегралом свертки



или же



Обычно доказательство данного положения выглядит так. Пусть на вход динамической системы подается произвольное входное воздействие x(t). Будем рассматривать значение выходной величины рассматриваемой системы в некоторый произвольный момент времени t.

С этой целью разобъем ось времени на достаточно малые отрезки длительности Δг каждый и построим график новой функции x’(t), совпадающей с x(t) в точках разбиения и остающейся постоянной в промежутках между ними (на рис.1 этот график показан пунктиром). Выбор такой аппроксимирующей функции объясняется двумя причинами:

1. Замена действительной функции x(t) приближенной x’(t) может быть осуществлена со сколько угодной высокой точностью, так как при Δг → 0 функция x’(t) стремится x(t)





2. Полагая, что система линейна, можно использовать свойство линейности (теорему сложения), согласно которому сигнал на выходе равен сумме реакций на отдельные импульсы.

Приближенная функция x’(t) может рассматриваться как последовательность прямоугольных импульсов длительности Δг каждый, что позволяет вычислить реакцию системы на воздействие x’(t) по известной реакции на прямоугольный импульс.

Обозначим: ğ(t) – реакция системы на прямоугольный импульс, имеющий длительность Δг и единичную площадь. Тогда сигнал на выходе системы в момент времени t можно представить как

Рисунок 1 – Входной сигнал и его аппроксимация ступенчатой функцией

1.3 Передаточная функция

- передаточная функция фильтра.



В общем случае для устойчивого и физически реализуемого ЦФ область сходимости передаточной функции будет включать единичную окружность и всю z-плоскость вне окружности, включая z=∞.

Область сходимости не содержит полюсов, значит для устойчивости надо, чтобы все полюса передаточной функции лежали внутри окружности 

Как известно ЦФ описывается разностным уравнением n-го порядка:



Воспользуемся свойством линейности:



Воспользуемся свойством сдвига последовательности:





Рассмотрим пример:

Пусть необходим ЦФ не пропускающий постоянную составляющую.







Возьмем z-преобразование от левой и правой части равенства:





 

Заключение

Обработка непрерывных сигналов заключается в преобразовании их свойств при помощи различных устройств и систем. Назовем простейшие виды преобразования сигналов: выпрямление, усиление, ограничение, фильтрация, модуляция, демодуляция и т.д.

Под непрерывной системой будем понимать техническое устройство, которая осуществляет преобразование непрерывного сигнала x(t) в другой непрерывный сигнал y(t) в соответствии с заданным оператором R (рис. 5.1).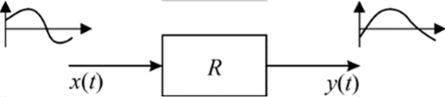



Рис. 2 Представление непрерывной системы

Система называется динамической, если текущее значение выходного сигнала зависит не только от текущих, но и более ранних значений внешних воздействий (входных сигналов).

Основная задача, которую приходится решать при анализе систем обработки сигналов, заключается в следующем. Дана система, с помощью которой преобразуется сигнал (рис. 5.1). На вход системы подается сигнал x(t). Требуется найти выходной сигнал у(1).

Преобразование входного сигнала x{t) в выходной сигнал y(t) описывается соотношением



где R_x и R_v - некоторые операторы, применяемые соответственно к функциям x(t) и y(t). Конкретный вид этих операторов зависит от характера преобразования сигнала, осуществляемого системой. Например, при выпрямлении будем иметь: j/(f)=|.x(f)|

В зависимости от вида оператора R непрерывные системы могут быть:

• 
  • линейными или нелинейными;
  
• 
  • стационарными или нестационарными;
  
• 
  • физически реализуемыми (каузальными) или нереализуемыми (некаузальными).
  

Линейность. Непрерывная система называется линейной тогда и только тогда, если ее операторы обладают свойствами аддитивности и однородности'.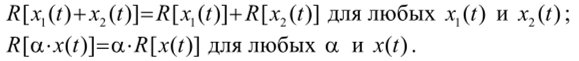



Эти свойства можно записать в виде одного условия:



Непосредственно из формулы легко видеть, что линейными операторами являются операторы умножения на постоянное число и суммирования. К линейным операторам относятся операторы интегрирования и дифференцирования: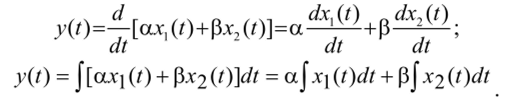



В то же время операторы логарифмирования или возведения в степень не обладают свойством линейности. Действительно: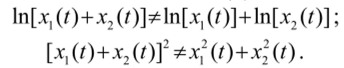



Ни одна реальная система преобразования сигналов, строго говоря, не удовлетворяет условиям линейности.

Стационарность. Стационарная система обладает следующим свойством: если реакция на входной сигнал x{t)равна у(Г)=/[х(/)], то для любого вещественного постоянного значения t₀ имеем y(t-t₀)=R[x(t-t₀)]. Это означает, что данное воздействие будет всегда приводить к одной и гой же реакции независимо от времени приложения воздействия.

Система называется стационарной (инвариантной во времени), если ее параметры не изменяются во времени.

Физическая реализуемость. Физически реализуемой называется система, у которой выходной сигнал в текущий момент времени не зависит от значений входного сигнала в последующие моменты времени.

Таким образом, еще раз скажем, что системы, которые могут быть описаны линейными дифференциальным уравнениями с постоянными коэффициентами, носят название линейных инвариантных во времени систем (ЛИВ–систем).

Линейные инвариантные во времени системы характеризуются следующими свойствами:

Свойство линейности и свойство неизменности (инвариантности) во времени.

Цель данной работы достигнута, все задачи выполнены.

Список литературы

1. 
   Коберниченко, В. Г. Основы цифровой обработки сигналов : учеб. пособие / В. Г. Коберниченко ; М-во науки и высш. образования Рос. Федерации, Урал. федер. ун-т. — Екатеринбург : Изд-во Урал. ун-та
   
2. 
   Тропченко А. Ю., Тропченко А. А. Цифровая обработка сигналов. Методы предварительной обработки. Учебное пособие по дисциплине" Теоретическая информатика" //СПб.: СПбГУ ИТМО. – 2009.
   
3. 
   Солонина А. И. Цифровая обработка сигналов в зеркале Matlab. – БХВ-Петербург, 2018.
   
4. 
   Маркович И. И. и др. Цифровая обработка сигналов в системах и устройствах //Ростов н/Д: Изд-во Южн. федерального ун–та. – 2012.
   
5. 
   Умняшкин С. Основы теории цифровой обработки сигналов. – Litres, 2018.
   
6. 
   Кутепов Н. И. и др. ПОЛУЧЕНИЕ СИГНАЛОВ И ИХ ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА //Информационные технологии, системный анализ и управление (ИТСАУ-2018). – 2018. – С. 182-186.
   
7. 
   Дегтярев А. Н., Харитонов В. Ф., Куня Э. ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ КАК УНИВЕРСАЛЬНЫЙ ВИД ЦИФРОВОЙ МОДУЛЯЦИИ //Современные проблемы радиоэлектроники и телекоммуникаций. – 2019. – №. 2. – С. 64-64.
   
8. 
   Борухов В. Т. Обращение линейных инвариантных во времени динамических систем с распределенными параметрами //Автоматика и телемеханика. – 1982. – №. 5. – С. 29-36.
   

Приложение 1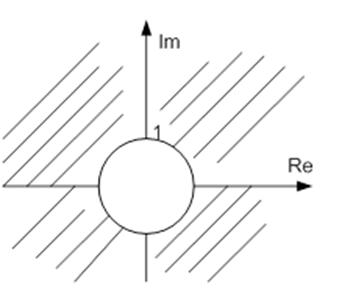