Лекция по технической механике. Тех. мех.. Количество движения системы (импульс системы)
 Скачать 61.55 Kb.
|
|
Количество движения системы (импульс системы). Количество движения (импульс тела) – векторная физическая величина, равная произведению массы тела на его скорость:  Импульс (количество движения) – одна из самых фундаментальных характеристик движения тела или системы тел. Запишем II закон Ньютона в другой форме, учитывая, что ускорение  Тогда  следовательно Произведение силы на время ее действия равно приращению импульса тела (рис. 1):  Где 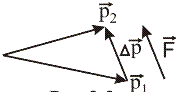 - импульс силы, который показывает, что результат действия силы зависит не только от ее значения, но и от продолжительности ее действия. Рис.1 Импульс силы Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Введем сначала понятие об элементарном импульсе, т. е. об импульсе за бесконечно малый промежуток времени dt. Элементарным импульсом силы называйся векторная величина  , равная произведению вектора силы  на элементарный промежуток времени   .Направлен элементарный импульс по линии действия силы. Импульс  любой силы за конечный промежуток времени t1 вычисляется как интегральная сумма соответствующих элементарных импульсов: .Следовательно, импульс силы за любой промежуток времени,  равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до .В частном случае, если сила и по модулю, и по направлению постоянна ( =const), будем иметь  . Причем, в этом случае и модуль  . В общем случае модуль импульса может быть вычислен через его проекции.Проекции импульса силы на прямоугольные декартовы оси координат равны:    .Единицей измерения импульса в СИ является –  Момент инерции Момент инерции является мерой инертности тела при вращательном движении тела. Мо 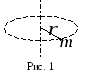 мент инерции материальной точки относительно неподвижной оси вращения равен произведению её массы на квадрат расстояния до рассматриваемой оси вращения (рис.1): . зависит только от массы материальной точки и её положения относительно оси вращения и не зависит от наличия самого вращения.Момент инерции - скалярная и аддитивная величина, поэтому момент инерции тела равен сумме моментов инерции всех его точек:  .В случае непрерывного распределения массы эта сумма сводится к интегралу:   ,где  - масса малого объема тела  ,  плотность тела,  - расстояние от элемента до оси вращения.Момент инерции является аналогом массы при вращательном движении. Чем больше момент инерции тела, тем труднее изменить угловую скорость вращаемого тела. Момент инерции имеет смысл только при заданном положении оси вращения. Бессмысленно говорить просто о “моменте инерции”. Он зависит : 1)от положения оси вращения; 2)от распределения массы тела относительно оси вращения, т.е. от формы тела и его размеров. Экспериментальным доказательством этого является опыт со скатывающимися цилиндрами. 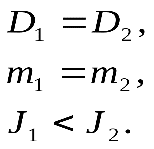 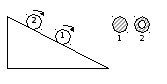 Произведя интегрирование для некоторых однородных тел, можно получить следующие формулы (ось вращения проходит через центр масс тела). Момент инерции обруча (толщиной стенок пренебрегаем) или полого цилиндра:   .Момент инерции диска или сплошного цилиндра радиуса R:   .Момент инерции шара   .Момент инерции стержня   .Ес  ли для тела известен момент инерции относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, находится по теореме Штейнера: момент инерции тела относительно произвольной оси равен моменту инерции J0 относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями. ,где d расстояние от центра масс О до оси вращения (рис.2). Центр масс - воображаемая точка, положение которой характеризует распределение массы данного тела. Центр масс тела движется так же, как двигалась бы материальная точка той же массы под действием всех внешних сил, действующих на данное тело. |