Исследование точности обработки с помощью кривых распределения
 Скачать 272.5 Kb.
|
 Исследование точности обработки с помощью кривых распределенияИсходные данные: результаты замеров двух выборок деталей, взятых с одного станка через некоторый промежуток времени. Æ 95 H9 Таблица 22
В каждой выборке находим наибольшее Xmax и наименьшее Xmin значения наблюдаемого параметра X и определяем размах варьирования по формуле: R =  .R1= 95,085-95 = 0,085 и R2= 95,085-95 = 0,085 . Разбиваем размах варьирования на 5 - 7 интервалов, m=5. Определяем цену интервала по формуле: C =   И .  ... Для построения гистограммы и кривой практического распределения заполняем таблицу 1. Подсчет частот по каждому интервалу удобно производить следующими способами. Слева выписывают интервалы от Xmin до Xmin +С; от Xmin +С до Xmin +2С и т.д. В каждый интервал включают размеры, лежащие в пределах от наименьшего значения интервала включительно, до наибольшего значения интервала, исключая его. Справа при помощи черточек подсчитывают число размеров по интервалам. Таблица 1 Расчет числа размеров по интервалам
По данным таблицы 1 для обеих выборок вычерчиваем гистограмму и полигон распределения 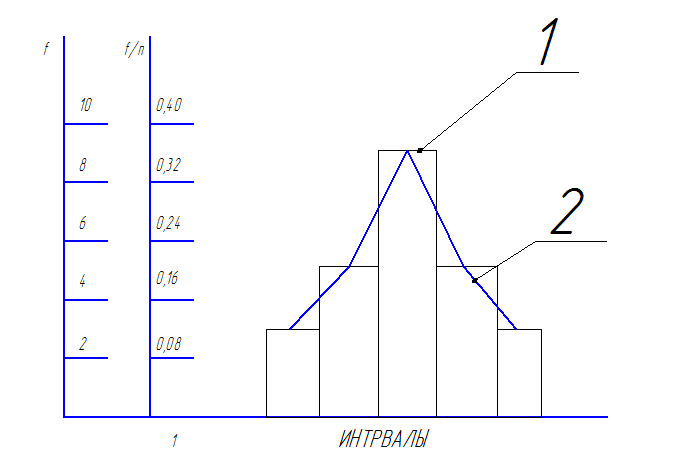 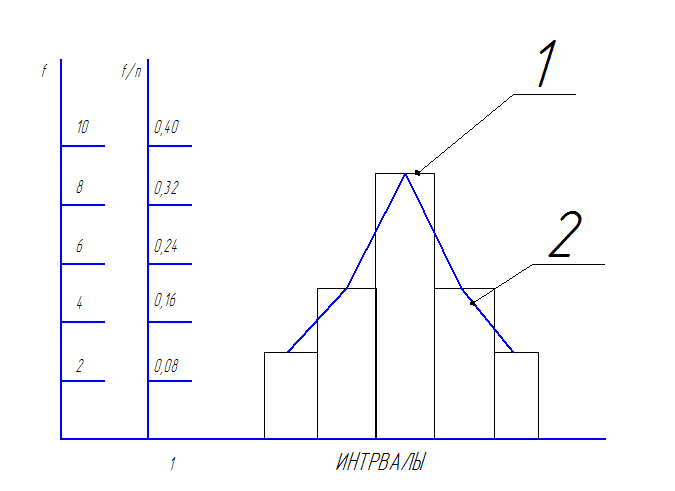 Рис.1 Гистограмма (1) и полигон (2) распределения. Для построения гистограммы по оси абсцисс откладывают интервалы, по оси ординат – соответствующие им частоты m или частость m/n. Последовательно соединяя между собой точки, соответствующие середине каждого интервала, получают эмпирическую кривую распределения. По внешнему виду эмпирической кривой распределения выдвигается гипотеза о распределении случайной величины. В нашем случае правомерна гипотеза о нормальном распределении, которое часто применяется при решении задач математической статистики и статистического анализа точности процесса обработки. Такое распределении, свидетельствует об устойчивости технологического процесса, так как замеры со значительными отклонениями от номинального размера встречаются редко. Выдвинутую гипотезу необходимо проверить. Чтобы найти и проверить закон распределения студенты рассчитывают числовые характеристики:
 .
 . где n- объем выборки; xi- найденные размеры. Вычисление среднеарифметического и среднеквадратичного отклонения при наличии обширных рядов измерений весьма трудоемко. Поэтому для удобства расчета статических характеристик составляют таблицу 2 предварительной обработки. Таблица2 Расчет статических характеристик измеряемых величин
Тогда расчет числовых характеристик можно осуществлять по формулам: 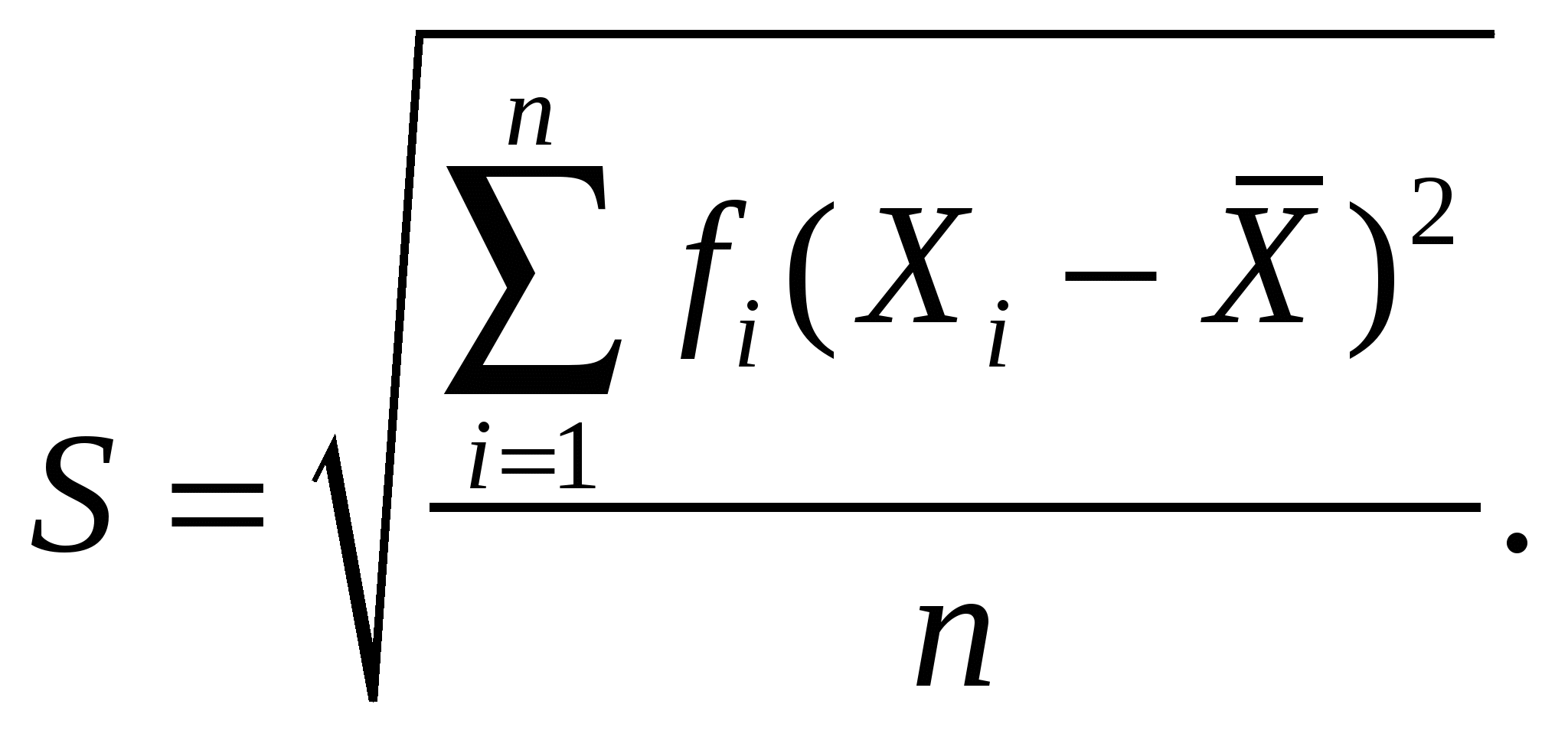  и  С учетом данных.приведенных в таблице 2, получим:  95,0425,  95,0425; S1 = 0,0198, S2 = 0,0198. Теперь следует проверить гипотезу нормальности распределения совокупности, из которой были взяты выборки. Для этого составляется вспомогательная таблица (табл.3) для вычисления критерия Колмагорова λ. Таблица 3 Промежуточные расчеты
В таблице 3 значение t вычисляется по формуле:  Значения Zt берутся из таблицы 4. Таблица 4 Нормальное распределение вероятностей
Значение  постоянно для всех значений Zt. Определяется  теоретическая частота для каждого интервала. Далее нужно вычислить  и  накопленные эмпирические и теоретические частоты, прибавляя к каждому значению  и  суммы предшествующих значений  или  .Критерий λ находим по формуле:  = 0,2 Для обеих выборок он будет одинаков и равен 0,536. По таблице 5 находим Р(λ)>1,что существенно превышает значение 0.05 и гипотеза нормальности кривой распределения размеров подтверждается. Таблица 5 Определение вероятности критерия λ
Если вероятность Р(λ) окажется очень малой ( практически, когда  ), то расхождение эмпирического и теоретического распределения считается существенным, а не случайным, и гипотеза о нормальности закона распределения величины X отвергается.4 Проверить возможность обработки партии деталей без брака по данным каждой выборки. 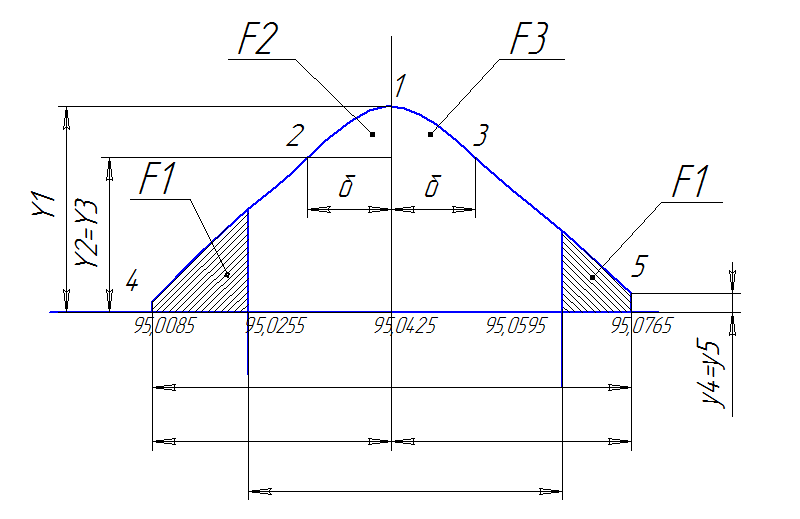 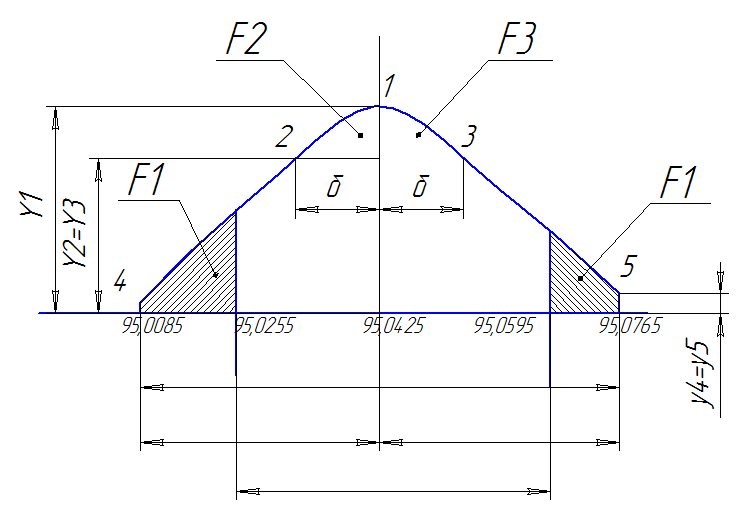 Строятся кривые распределения  Рис. 2. Кривая нормального распределения ордината точки 1 определена при   (8)ординаты точек 2 и 3 определены на расстоянии  от центра группирования (9)ординаты точек 4 и 5 на расстоянии  от центра группирования принимаются равными нулю т.е. ; (10)где С - величина интервала, вводится для приведения кривой нормального распределения к тому же масштабу, в котором вычерчен эмпирический полигон распределения. Численные значения ординат пяти характерных точек приведены в таблице ниже
Проверяем возможность обработки наружной поверхности диаметром Ø95H9+0.087 без брака по данным каждой выборки. Определяем фактическое поле рассеивания по формуле:  Соответственно, для каждой выборки имеем:  =6 0.0198=0,1188 и  60,0198=0,1188. Располагаем на кривой распределения (рис.1) наименьший размер dнм=95,000, наибольший размер dнб=95,085 и допуск размера детали Т=0,087. Обработка без брака возможна, если фактическое поле рассеивания не выходит за границы поля допуска. В данном случае обработка без брака невозможна. Вероятный процент брака всей партии обработанных деталей определяется следующим образом ( рис. 2 ). Процент годных деталей определяется площадью, ограниченной кривой и осью абсцисс на длине, равной допуску т.е. Q =  где   ; и   Процент получения неисправимого брака  ; процент получения исправимого брака  где  и  - функция Лапласа. Значения этой функции табулированы в зависимости от величины t и приведены в таблице 3. Результаты расчета по приведенным формулам приводим ниже.
Проверяем равенство точности обработки и неизменность настроечного размера в обеих выборках. Учитывая, что  и S1= S2, следует считать, что неизменность настроечного размера и равенство точности обработки соблюдаются. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2
