ЛР2. Laboratornaya_rabota_N2_-_na_proverku__860412проверено. ЛР2 Экспериментальная проверка основного закона динамики вращательного движения. Определение момента инерции тела относительно оси, проходящей через центр масс тела
 Скачать 117.03 Kb. Скачать 117.03 Kb.
|
|
ЛР№2 Экспериментальная проверка основного закона динамики вращательного движения. Определение момента инерции тела относительно оси, проходящей через центр масс тела.Таблица 1
Таблица 2
Дано. Высота первоначального подъёма маятника - она в данной работе постоянна и равна h=0.4м. Цена деления линейки при определении высоты равнялась 1 см=0.01 м. Диаметр стержня – оси маятника в данной работе был измерен штангенциркулем с приборной погрешностью Dd=0.0001 м. Dd=0.0001 м. Масса маятника в данной работе определена при взвешивании тела на весах с точностью Dm=0.01 кг. Приборная погрешность секундомера составляет 0.001 с. Формулы и расчеты (m1): Вычисляем среднее значение времени <t>. Находим отклонения каждого из пяти измерений t1 от среднего значения времени <t>. Возводим в квадрат каждое отклонение и просуммируем квадраты отклонений. Рассчитываем среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной оценки S( 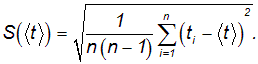 Буквой n обозначено число измерений, в нашем случае n=5 S( 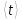 )=√ )=√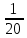 x0,0003652= x0,0003652=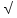 0.00001826=0,004273172 с 0.00001826=0,004273172 сУмножив вычисленное значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени: где tP(n) – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n= n-1. Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 из таблицы коэффициентов Стьюдента находим t0.9(5-1)=2.13. ∆t=2,13х0,004273172=0,009101856 Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается. Тогда результат измерения времени t запишем в виде: t1=(4,435±0,009)с Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле Et= 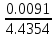 x100%=0.2% x100%=0.2%Вычислите момент инерции маятника по формуле 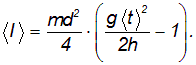 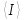 = = 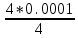 * ( * (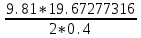 - 1) = 0.0001*240.237375 = 0.0240237 кг·м² - 1) = 0.0001*240.237375 = 0.0240237 кг·м²Рассчитайте относительную EI и абсолютную DI погрешности соответственно по формулам 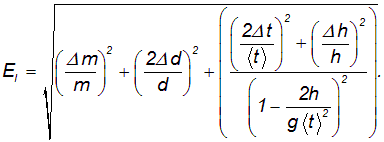 E1 = 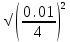 + +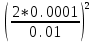 + ( + (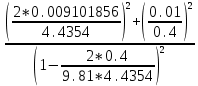 ) = ) = 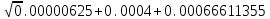 = = 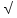 0.00107236355 = 0.032746962 0.00107236355 = 0.032746962∆I=0.032746962*0,0240237=0.0007867 кг/м2 I1=(0,0240±0,0008) кг/м2 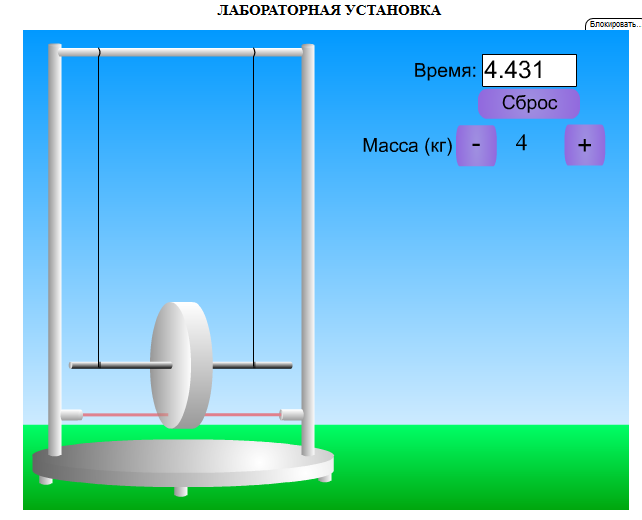 Таблица 3
Таблица 4
Формулы и расчеты (m2): Вычисляем среднее значение времени <t>и вносим данные в таблицу. Находим отклонения каждого из пяти измерений t2 от среднего значения времени <t>. Возводим в квадрат каждое отклонение и просуммируем квадраты отклонений. Рассчитываем среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной оценки S( 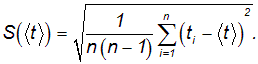 Буквой n обозначено число измерений, в нашем случае n=5 S( 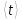 )=√ )=√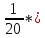 0,0003028= 0,0003028=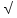 0.00001514=0,003891015 с 0.00001514=0,003891015 сУмножив вычисленное значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени: где tP(n) – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n= n-1. Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 из таблицы коэффициентов Стьюдента находим t0.9(5-1)=2.13. ∆t=2,13х0,003891015=0,00828786 с Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается. Тогда результат измерения времени t запишем в виде: t2=(4,432±0,008)с Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле Et= 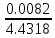 x100%=0.19% x100%=0.19%Вычислите момент инерции маятника по формуле 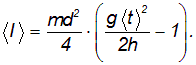 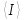 = = 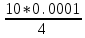 * ( * (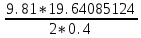 - 1) = 0.00025*239,845938 = 0.05996148 кг·м² - 1) = 0.00025*239,845938 = 0.05996148 кг·м²Рассчитайте относительную EI и абсолютную DI погрешности соответственно по формулам 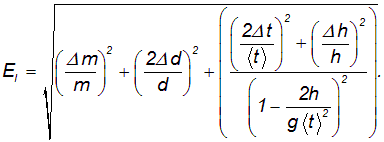 E1 = 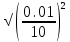 + +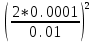 + ( + (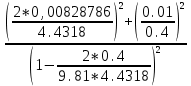 ) = ) = 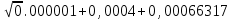 = = 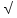 0.00106417 = 0.0326216 0.00106417 = 0.0326216∆I=0.0326216*0.05996148=0,001956039 кг/м2 I2=0.060±0,002 кг/м2 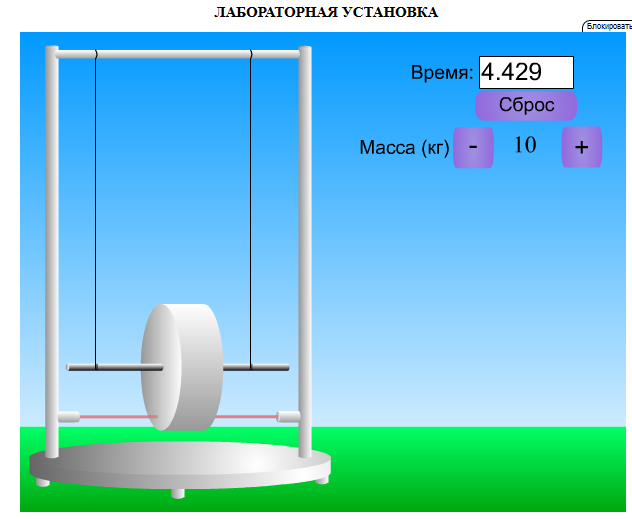 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
