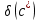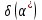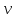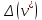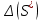Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата Вариант 25. лабораторная работа 1. Отчёт по лабораторной работе 1 Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата Вариант 25 Теоретическая часть
 Скачать 345.89 Kb. Скачать 345.89 Kb.
|
|
Отчёт по лабораторной работе № 1 Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата Вариант 25 Теоретическая часть Различают 2 вида погрешностей – абсолютную и относительную. О - абсолютная погрешность числа равна модулю разности точного и приближенного значения этого числа. О - Относительная погрешность не зависит от масштаба величины единицы измерения. Часто задают верхние оценки погрешностей, потому что непосредственные вычисления по формулам невозможны.  О З Значащую цифру числа называют верной, если Существует два вида округления: 1) усечение – отбрасывание всех цифр, расположенных правее n-ой значащей цифры. Погрешность не превышает единицы того же разряда; 2) округление по дополнению. Это правило: если первая цифра слева из отбрасываемых меньше 5, то эти цифры просто отбрасываются как при усечении; если же первая цифра слева из отбрасываемых больше или равна 5, то младший сохраняемый разряд увеличивается на 1. Абсолютная величина погрешности по дополнению не превышает половины единицы последней оставляемой значащей цифры. Для оценки относительных погрешностей результата при умножении и делении формулы используются редко. Обычно на практике выполняются условия 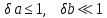 и используется приближенное равенство и используется приближенное равенство . . Таким образом, практически при умножении и делении приближенных чисел их относительные погрешности складываются. Задание № 1. Величина подъемной силы крыла самолета оценивается по формуле  где где 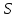 - площадь проекции крыла на горизонтальную плоскость, - площадь проекции крыла на горизонтальную плоскость,  - плотность атмосферы на заданной высоте, - плотность атмосферы на заданной высоте,  - угол атаки, отсчитываемый от направления нулевой подъемной силы, - угол атаки, отсчитываемый от направления нулевой подъемной силы,  - коэффициент, зависящий от формы крыла. Требуется вычислить - коэффициент, зависящий от формы крыла. Требуется вычислить  при заданных значениях при заданных значениях 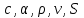 и заданных абсолютных или относительных значениях этих величин. и заданных абсолютных или относительных значениях этих величин.Таблица 1( В таблице 1 для нечетных вариантов задано 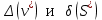 , для четных , для четных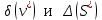 ) )
Решение: Пусть с = 0.005, δ(с*) = 0.01, α = 12, δ(α)=0.01, ρ = 0.89, δ(ρ*) = 0.01, ν = 400, Δ(ν*) = 5, S = 20, δ(S*) = 0.001 δ(ν*) =  = =  = 0.0125 = 0.0125Относительная погрешность функции  равна равна Так как относительная погрешность велика, то значение функции следует вычислять не более чем с двумя – тремя знаками (с запасом), то есть   Абсолютная погрешность равна 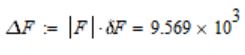 Поскольку 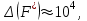 то результат целесообразно округлить до двух знаков. Окончательно, то результат целесообразно округлить до двух знаков. Окончательно,  Задание №2 Дано: 
Абсолютные погрешности аргументов даны: 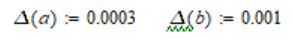 Относительные будут равны:   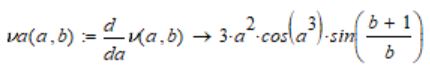 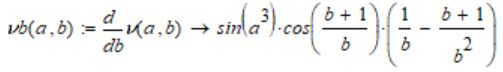  По формуле 1.4.2 получим:  Само значение функции равно: 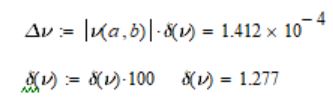 Абсолютные погрешности аргументов даны: Относительные будут равны: 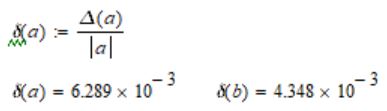 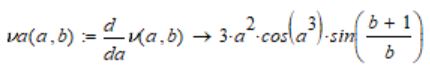 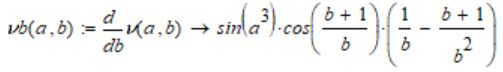  По формуле 1.4.2 получим:  Само значение функции равно:  Абсолютные погрешности аргументов даны: Относительные будут равны:  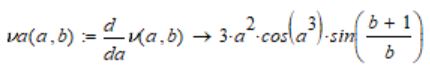 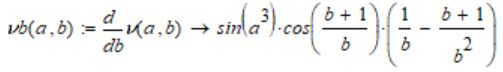  По формуле 1.4.2 получим:  Само значение функции равно:  |