тор. Интегральное исчисление функций одного переменного
 Скачать 127.56 Kb. Скачать 127.56 Kb.
|
Интегральное исчисление функций одного переменногоНЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Опр. Функция 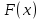 называется первообразной функции называется первообразной функции 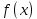 на на 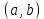 , если , если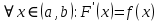 . .Пример. 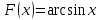 – первообразная функции – первообразная функции 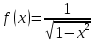 на интервале на интервале 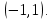 Теорема 1 (об арифметических свойствах первообразной). Пусть 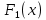 и и 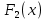 – первообразные функций – первообразные функций 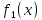 и и 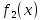 соответственно. Тогда функция соответственно. Тогда функция 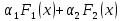 – первообразная функции – первообразная функции 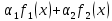 ( (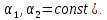 Док-во: 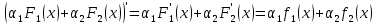 , т.е. функция , т.е. функция 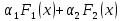 – первообразная функции – первообразная функции 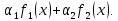  Теорема 2 (об общем виде первообразной). Пусть 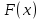 – первообразная функции – первообразная функции 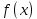 . Тогда любая первообразная функции . Тогда любая первообразная функции 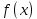 имеет вид имеет вид 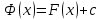 , где , где 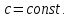 Док-во: т.к. 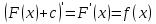 , , то 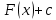 – тоже первообразная функции – тоже первообразная функции 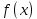 . Покажем, что любая первообразная имеет вид . Покажем, что любая первообразная имеет вид 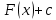 . . Пусть 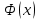 – первообразная функции – первообразная функции 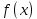 . Рассмотрим функцию . Рассмотрим функцию 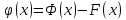 : : 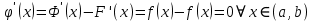 . Рассмотрим произвольные . Рассмотрим произвольные 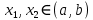 . . 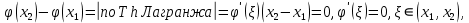 т.е. т.е. 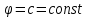 . Значит, . Значит, 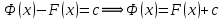  Опр. Множество всех первообразных функции 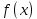 называется неопределенным интегралом от функции называется неопределенным интегралом от функции 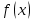 . .Обозначение: 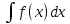 . .Пусть 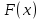 – первообразная функции – первообразная функции 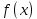 . Тогда . Тогда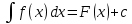 , где , где 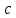 – произвольная постоянная. – произвольная постоянная.Пример. 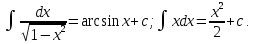 Свойства неопределенного интеграла: 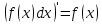 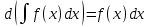 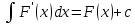 или или 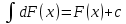 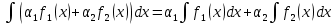 , где , где 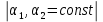 Док-во: 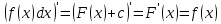 , где , где 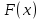 – первообразная функции – первообразная функции 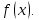 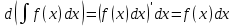 . .Т.к. 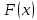 – первообразная – первообразная 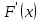 , то , то 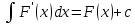 . .Пусть 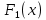 и и 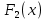 – первообразные функций – первообразные функций 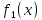 и и 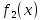 соответственно. соответственно. Тогда функция 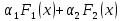 – первообразная функции – первообразная функции 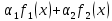 ( (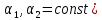 . Отсюда . Отсюда 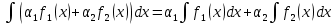  Таблица интегралов: 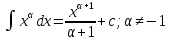 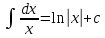 . (Т.к. при . (Т.к. при  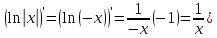 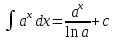 ( (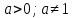 ) )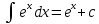 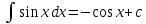 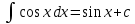 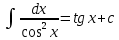 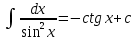 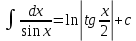 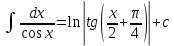 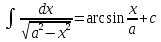 , , 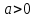 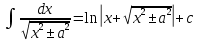 , , 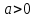 (длинный логарифм) (длинный логарифм)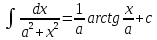 , , 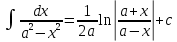 или или 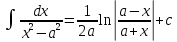 (высокий логарифм) (высокий логарифм)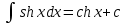 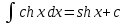 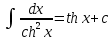 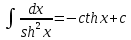 Примеры. 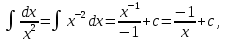 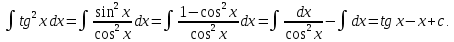 Интегрирование подстановкой и по частям.Подведение под знак дифференциала Пусть 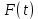 – первообразная функции – первообразная функции 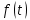 на на 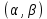 , т.е. , т.е.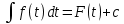 . .Рассмотрим замену 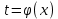 , где , где 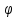 – дифференцируемая на – дифференцируемая на 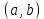 функция, функция, 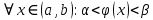 . .Рассмотрим сложную функцию 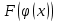 , , 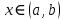 . Тогда имеем: . Тогда имеем: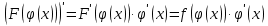 , ,т.е. 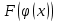 – первообразная для – первообразная для 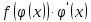 , т.е. , т.е.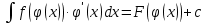 , ,или 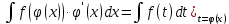 , , или 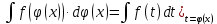 , , 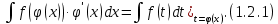 Примеры.  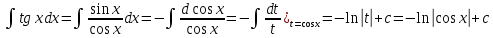 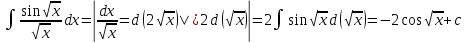 . .Замена переменной Поменяем в (1.2.1) местами 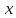 и и 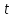 : : 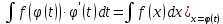 , ,где 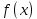 определена на определена на 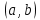 , , 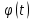 дифференцируема на дифференцируема на 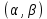 , причем , причем 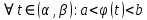 . .Пусть 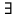 обратная функция обратная функция 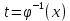 . Заменим . Заменим 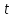 на на 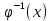 : :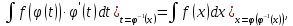 Т.е. 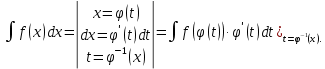 Примеры.  =  Интегрирование по частям Пусть функции 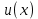 и и 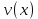 дифференцируемы на дифференцируемы на 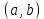 . Тогда . Тогда 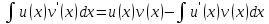 , т.е. , т.е. 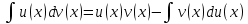 Док-во: 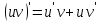 , т.е. , т.е. 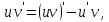 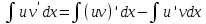 , , т.е. 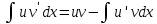 , ,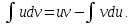  Примеры.  = = 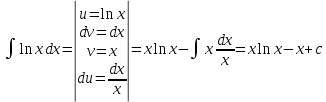 . .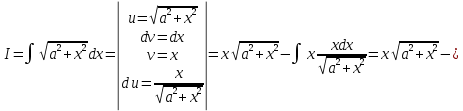 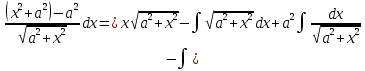 , ,Следовательно: 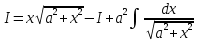 , ,т.е. 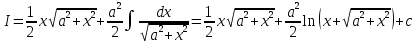 . .Интегрирование выражений, содержащих квадратный трехчлен 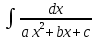 , , 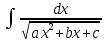 . .Выделим полный квадрат, получим табличный интеграл (10-13) Примеры. 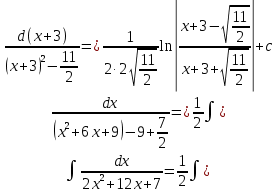 . .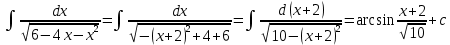 . .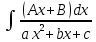 , , 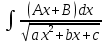 . .Выделим в числителе производную квадратного трехчлена 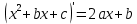 , т.е. представим числитель в виде , т.е. представим числитель в виде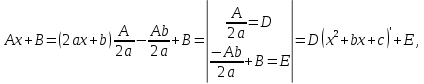 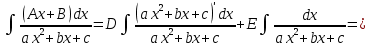 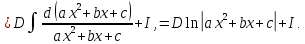 где 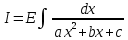 – находится с помощью выделения полного квадрата. – находится с помощью выделения полного квадрата.Аналогично 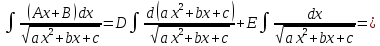 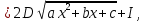 где 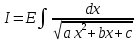 . .Примеры. 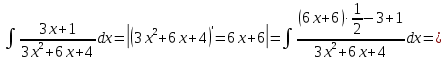 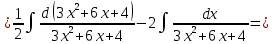 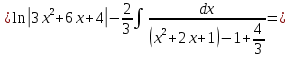 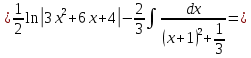 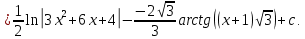 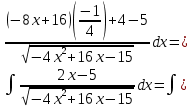 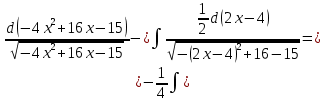 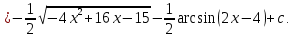 Интегрирование тригонометрических функций 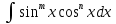 , где , где 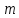 или или 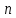 – нечетное натуральное число (например, – нечетное натуральное число (например, 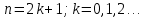 ) )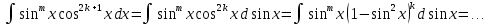 Пример. 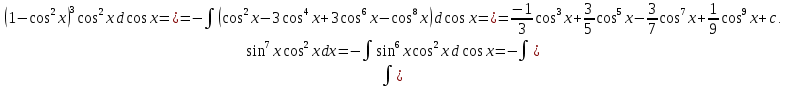 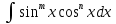 , где , где 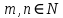 – четные. Используем формулы понижения степени – четные. Используем формулы понижения степени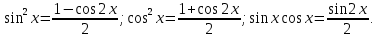 Пример. 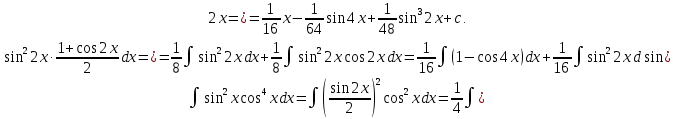 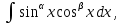 где где 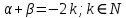 (т.е. (т.е. 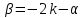 ). Используем формулы ). Используем формулы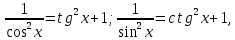 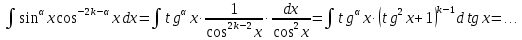 Пример. 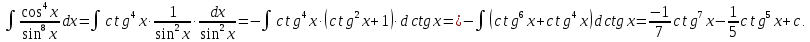 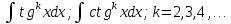 . Понижение показателя с использованием формул . Понижение показателя с использованием формул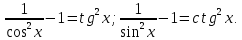 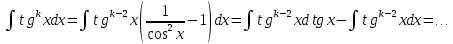 Пример. 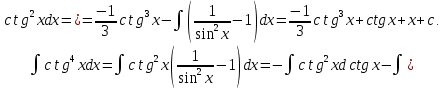 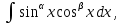 где где 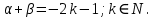 Понижение степени с использованием формул: Понижение степени с использованием формул: 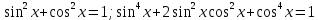 и т.д. и т.д.Пример. 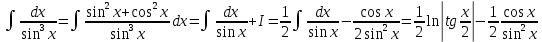 +c, +c,где 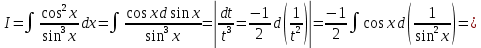 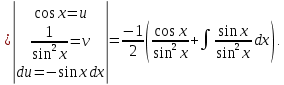 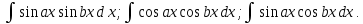 Преобразование произведения тригонометрических функций в сумму. 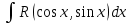 , где , где 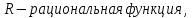 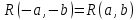 . .Подстановка 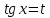 . .Пример. 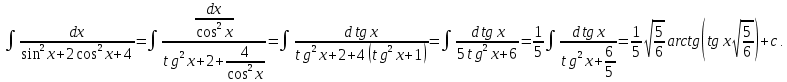 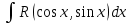 , где , где 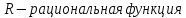 . .Подстановка 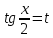 , ,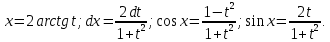 Пример. 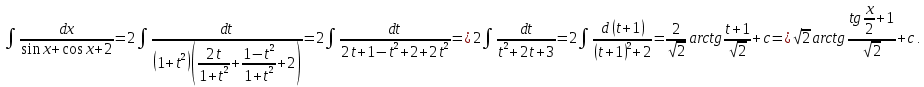 Интегрирование иррациональных функций 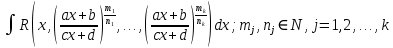 . .Замена 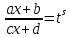 , , 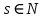 –общий знаменатель –общий знаменатель 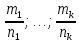 (Н.О.К. (Н.О.К. 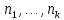 ). ).Пример. 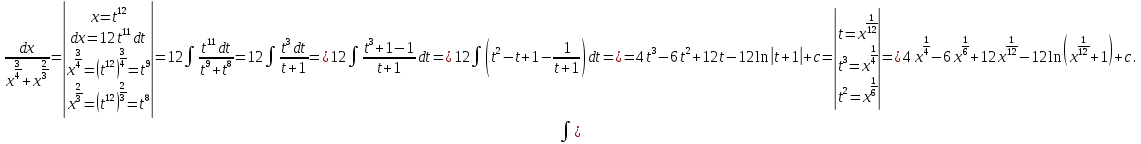 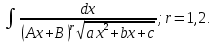 Замена 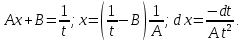 Пример. 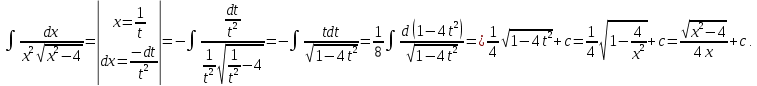 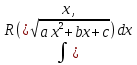 . .Выделив полный квадрат, получим интеграл одного из видов: 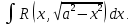 Замена 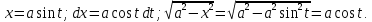 Пример. 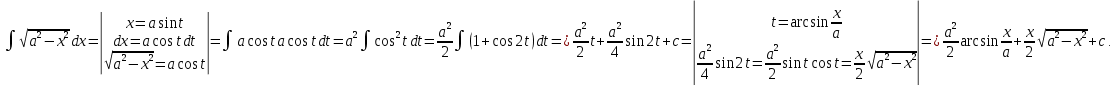 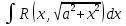 . .Замена 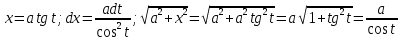 . .Пример. 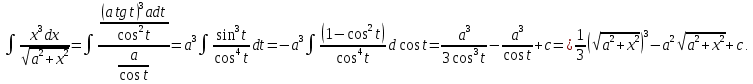 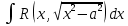 . .Замена 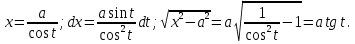 Пример. 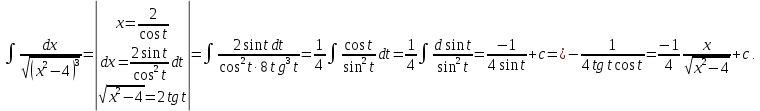 Примеры интегралов, не выражающихся через элементарные функции: 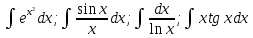 («неберущиеся» интегралы). («неберущиеся» интегралы). |
