Дизъюнктивная и конъюнктивная совершенные нормальные формы
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
Дизъюнктивная и конъюнктивная совершенные нормальные формы Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону. Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной. Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом). Совершенная дизъюнктивная нормальная форма (СДНФ) Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний. Примеры: y, ¬ y, х1 ∧ ¬ х2 ∧ х3 ∧ х4 Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записывается в следующей форме: F1 ∨ F2 ∨ ... ∨ Fn, где Fi - элементарная конъюнкция Примеры: ¬ х1 ∧ х2 ∨ х1 ∧ ¬ х2 ∨ х1 ∧ ¬ х2 ∧ х3, ¬ y1 ∨ y1 ∧ y2 ∨ ¬ y2 Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если: 1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой конъюнкции стоит либо переменная хi, либо ее отрицание; 2) все элементарные конъюнкции в такой ДНФ попарно различны. Пример: (¬ х1 ∧ х2 ∧ х3) ∨ (х1 ∧ ¬ х2 ∧ х3) ∨ (х1 ∧ х2 ∧ ¬ х3) Совершенная конъюнктивная нормальная форма (СКНФ) Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний. Примеры: ¬ х3, х1 ∨ х2, х1 ∨ х2 ∨ ¬ х3 Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций. КНФ записывается в следующей форме: F1 ∧ F2 ∧ ... ∧ Fn, где Fi - элементарная дизъюнкция Примеры: (х1 ∨ ¬ х2) ∧ х3, (х1 ∨ х2) ∧ ( ¬ х1 ∨ х2 ∨ х3) ∧ ( х1 ∨ ¬ х2 ∨ ¬ х3) Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если: 1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой дизъюнкции стоит либо переменная хi, либо ее отрицание; 2) все элементарные дизъюнкции в такой КНФ попарно различны. Пример: (х1 ∨ х2 ∨ х3) ∧ ( ¬ х1 ∨ ¬ х2 ∨ х3) Заметим, что любую логическую функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ. Алгоритм построения СДНФ по таблице истинности 1.Выбрать все строки таблицы, в которых значение функции равно единице. 2.Для каждой такой строки записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание. 3.Все полученные конъюнкции связываем операциями дизъюнкции. Алгоритм построения СКНФ по таблице истинности Выбрать все строки таблицы, в которых значение функции равно нулю. 2.Для каждой такой строки записать дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание. 3.Все полученные дизъюнкции связываем операциями конъюнкции. Анализ алгоритмов показывает, что если на большей части строк таблицы истинности значение функции равно 0, то для получения ее логической формулы лучше построить СДНФ, в противном случае - СКНФ. Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию. 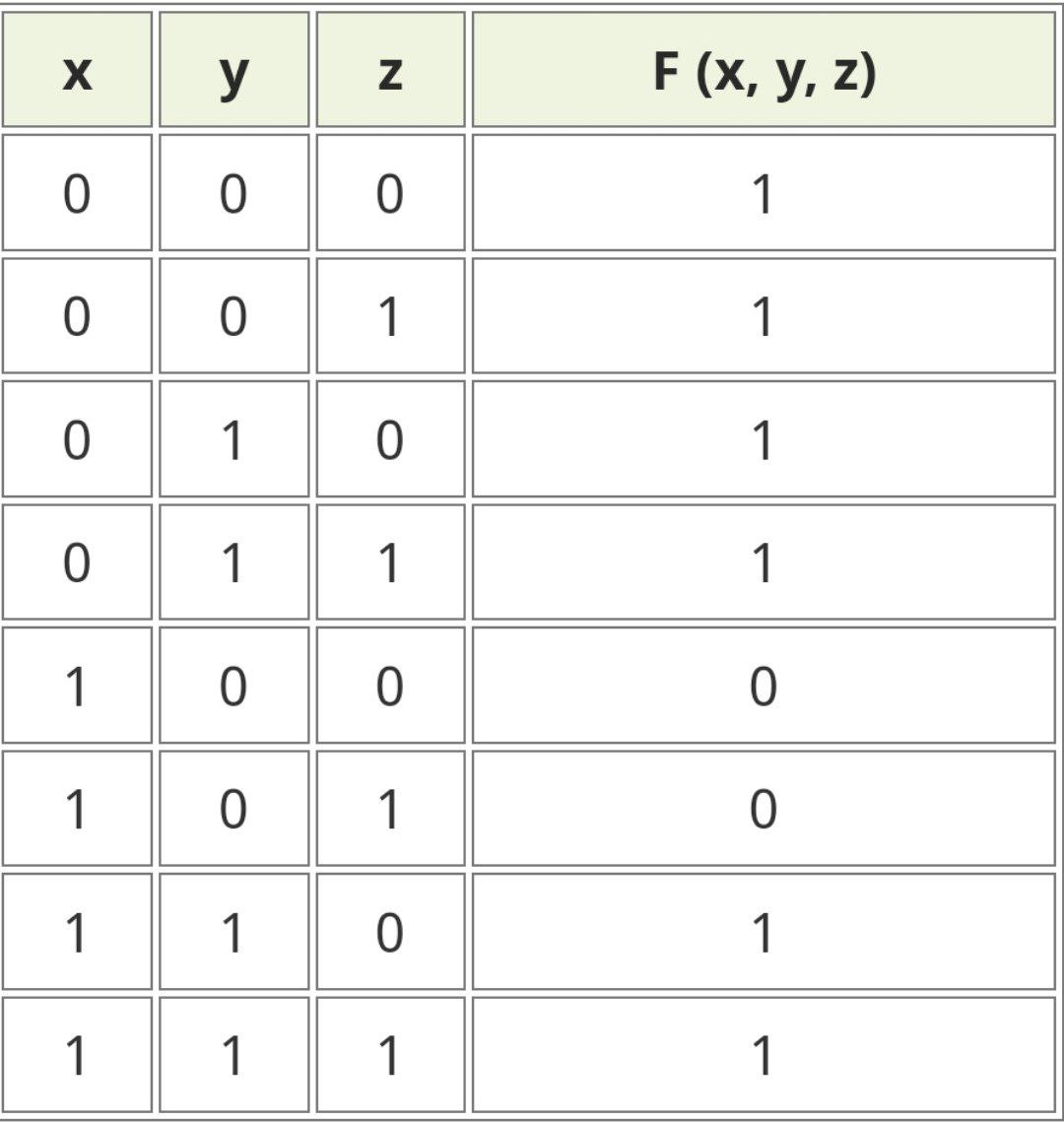 Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу: F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z) Проверим полученную формулу. Для этого построим таблицу истинности функции. Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно. 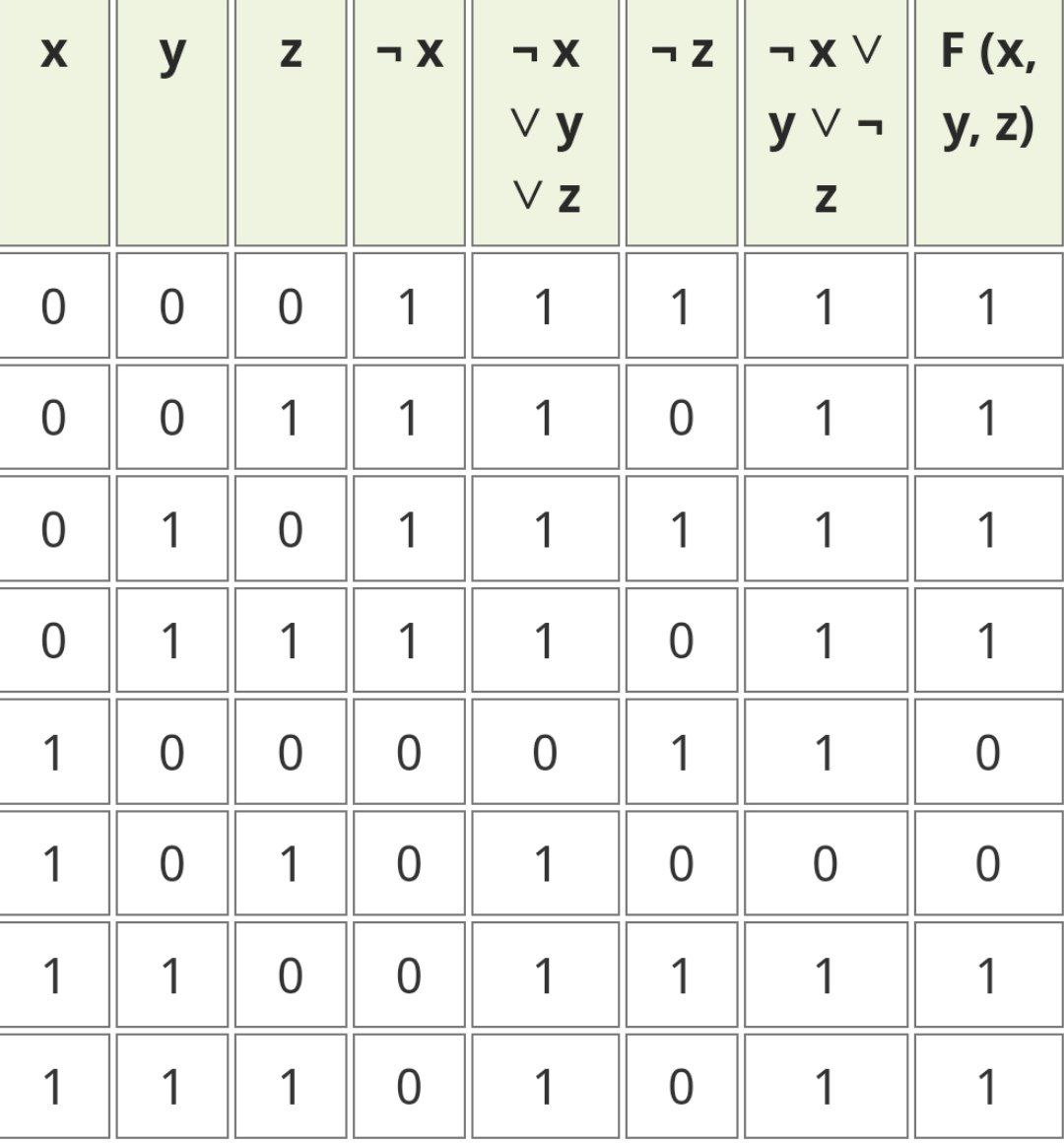 Построение СКНФ и СДНФ по таблице истинности Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации. Выделяют такие виды формы нормального типа: •КНФ (конъюнктивная нормальная форма), где подразумевается конъюнкция того или иного количества дизъюнкций, как пример, (A∨ 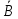 ∨C)Λ(A ∨C); ∨C)Λ(A ∨C);•ДНФ (дизъюнктивная нормальная форма), где осуществляется дизъюнкция конъюнкций, как пример, . (A Λ 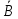 Λ C) ∨ (A Λ C); Λ C) ∨ (A Λ C);СКНФ Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия: •отсутствие одинаковых элементарных дизъюнкций; •дизъюнкции не содержат одинаковые переменные; • все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа. Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице. СДНФ Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия: • отсутствие одинаковых элементарных конъюнкций; • конъюнкции не свойственно обладать одинаковыми переменными; в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму. При этом в одинаковом порядке. Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте. Построение СДНФ согласно таблице истинности Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю. Нахождение СКНФ и СДНФ: Примеры Согласно таблице истинности записать логическую функцию: 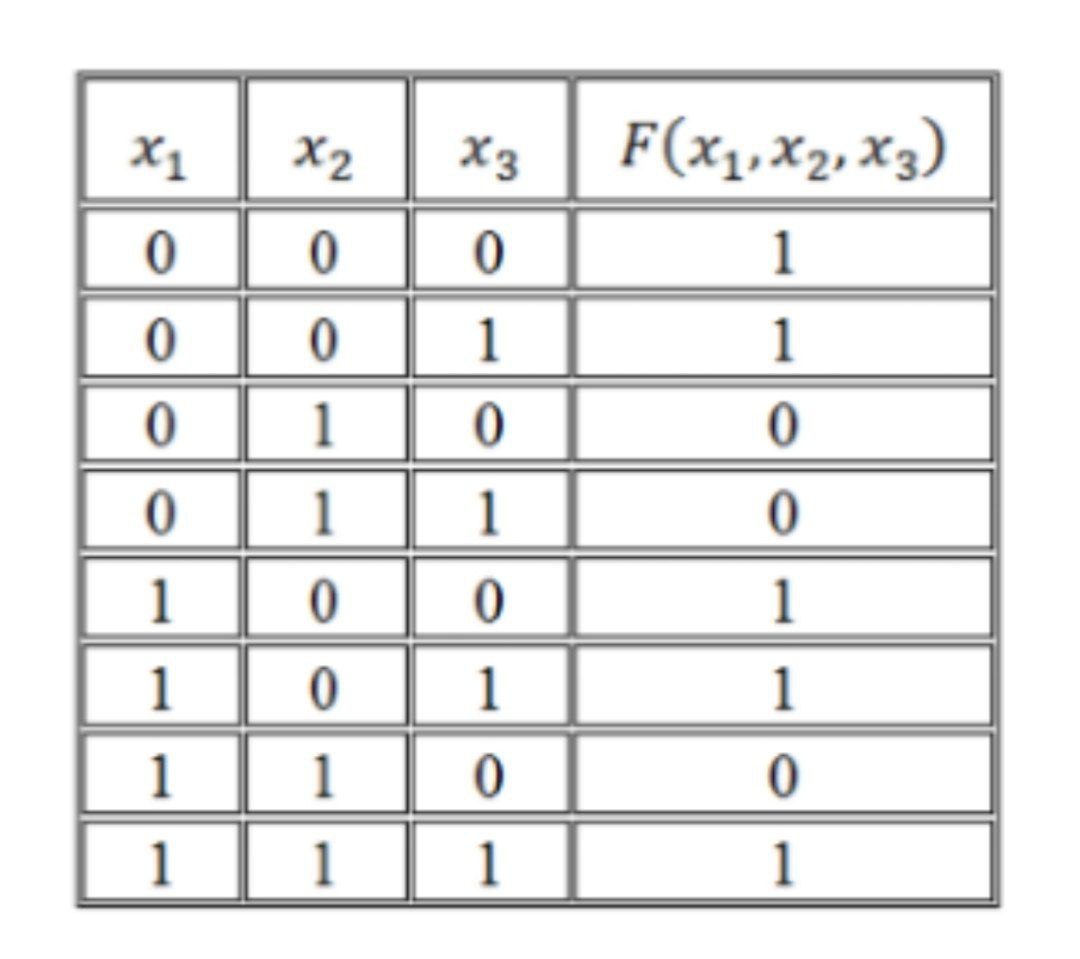 РЕШЕНИЯ Прибегнем к правилу построения совершенной ДНФ 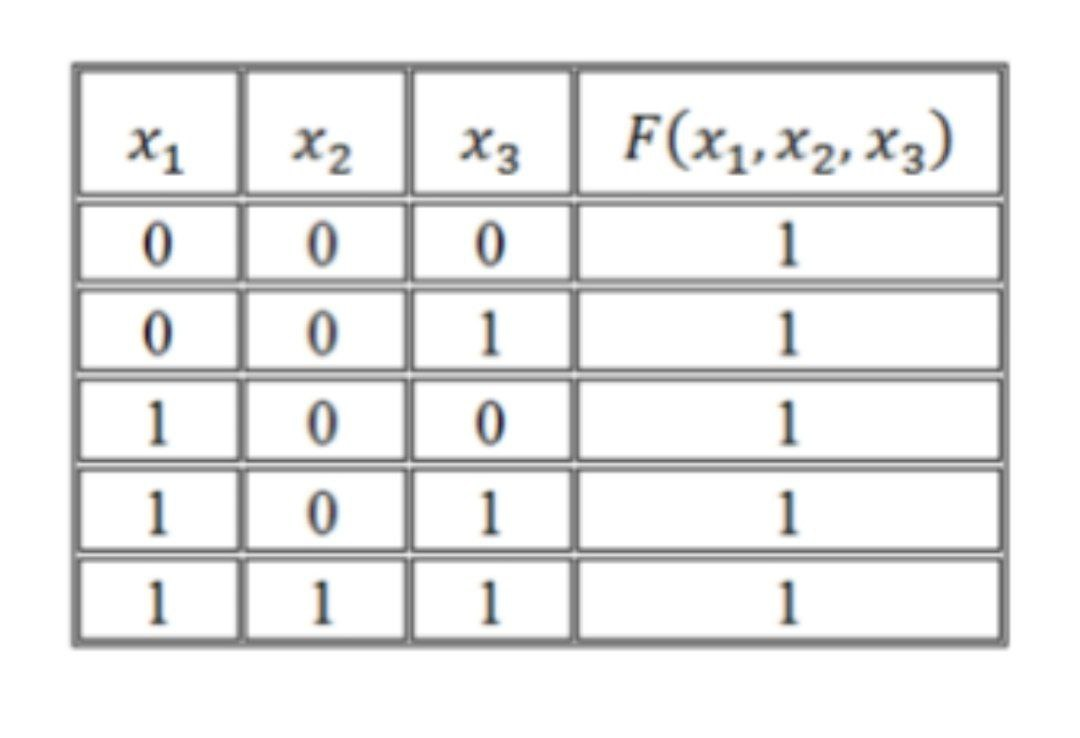 Получаем такую СДНФ F(x1 ,x2,x3)= ( 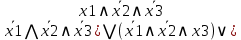 ) )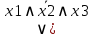 ) ) 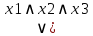 ) )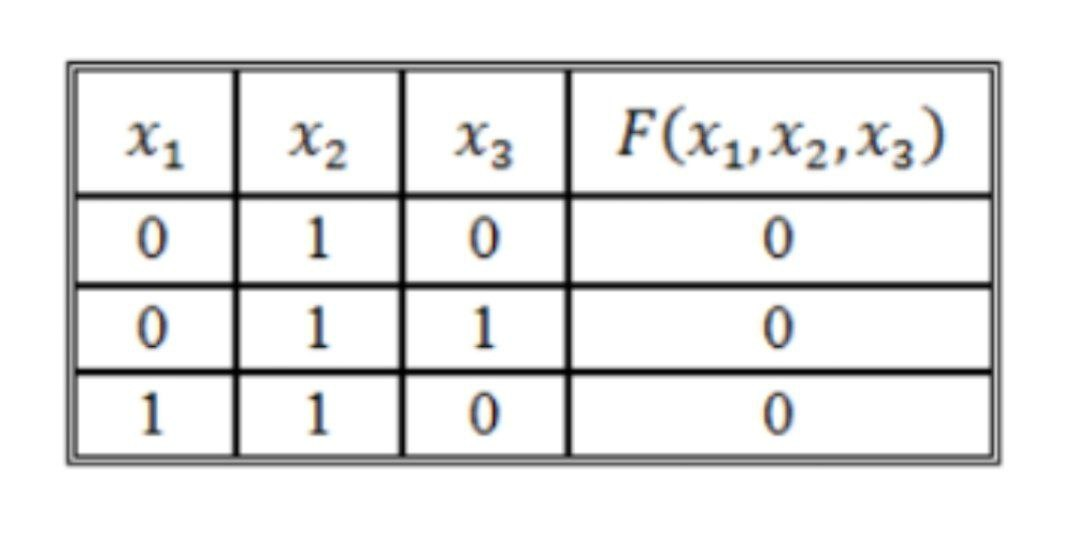 Задействовав правило её построения Задействовав правило её построенияПолучаем СКНФ F(x1 ,x2,x3)= ( 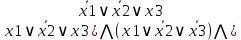 |
