Джозефсоновский переход
 Скачать 233.04 Kb. Скачать 233.04 Kb.
|
|
Джозефсоновский переход Рассмотрим замкнутую цепь с источником постоянного тока и джозефсоновским туннельным контактом(ДжК). В большинстве случаев ДжК представляет собой два сверхпроводящих электрода, которые разделенны между собой тонким слоем диэлектрика. Если величина протекающего постоянного тока в замкнутой цепи меньше величины критического тока на ДжК, то такой ток протекает без потерь. В таком случае ток через ДжК протекает последовательно, за счет куперовских пар. Но у величины сверхтока есть определенный предел, который равен критическому току джозефсоновского контакта. Если по замкнутой цепи течет ток, значение которого превышает величину крит.тока ДжК, то такой ток не может идти только за счет пар – возникает ток нормальной компоненты электронов и за счет этого возникает падение напряжение. Таким образом, джозефсоновский переход можно представить как параллельное включение собственно самого ДжК и нормального участка с активным сопротивлением. Фундаментальные соотношения Джозефсона В начале рассмотрим стационарный эффект Джозефсона. При протекании слабого тока через ДжК не возникает падения напряжения т.е. ток течет бездиссипативно за счет сверхпроводящих носителей. Ток через такой переход описывается соотношением: 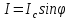 , (1.1)* , (1.1)*где 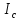 - критический ток ДжК - критический ток ДжК*Как получилось выражение для тока на ДжК? Для этого необходимо рассмотреть геометрию в которой два сверхпроводника разделены тонким слоем диэлектрика(Рис) 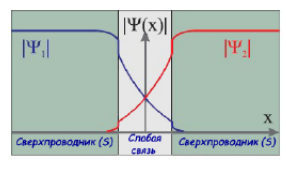 Рисунок Перекрытие волновых функций в SIS контакте В пределах перехода величины волновых функций падают экспоненциально поскольку они входят в изоляционную область, но сохраняют свои фазы. Для получения (1.1) рассмотрим функцию плотности тока( 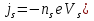 , подставим ее в ток вероятности и получим: , подставим ее в ток вероятности и получим: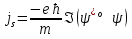 Здесь волновая функция �� является суперпозицией двух волновых функций на переходе:  , где , где 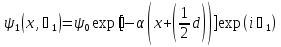 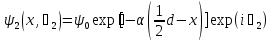 Подставляя это в выражение для тока вероятности, взяв при этом мнимую часть от произведения 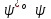 , получим: , получим: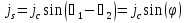 ,где ,где  Перейдем к рассмотрению нестационарного эффекта Джозефсона. Он возникает, в случае если заданный внешней цепью постоянный ток превысит значение 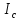 и на ДжК возникнет напряжение V. Поскольку туннелирование электронов через контакт является квантовым эффектом, рассмотрим волновое уравнение Шредингера: и на ДжК возникнет напряжение V. Поскольку туннелирование электронов через контакт является квантовым эффектом, рассмотрим волновое уравнение Шредингера: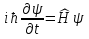 (1.2) (1.2)Волновую функцию 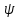 можно представить в виде произведения пространственных и временных координат можно представить в виде произведения пространственных и временных координат 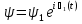 .Подставляя это выражение в (1.2) и воспользовавшись методом разделения переменных для временной координаты найдем, что .Подставляя это выражение в (1.2) и воспользовавшись методом разделения переменных для временной координаты найдем, что 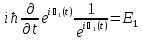 Отсюда получим 1-ое соотношение Джозефсона: 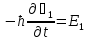 Аналогично для волновой функции находящейся на противоположном “берегу”: 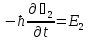 Поскольку на ДжК возникло напряжение V, то энергию, которые приобрели сверхпроводящие носители, туннелируя через переход, можно записать в виде: 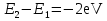 Отсюда получим 2-ое соотношение Джозефсона 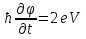 ,где ,где 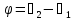 Таким образом, если ток в замкнутой цепи превышает критическое значение, джозефсоновский переход можно описать в рамках резистивной модели(Рис).  Используя Если ток на ДжК превышает значение критического тока, то на контакте возникает переменное напряжение. Разрыв носителей заряда на туннельном контакте При значении тока ток на ДжК превышает значение 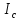 и возникает нормальная компонента электронов. По какому принципу происходит распад сверхпроводящих носителей заряда?Для этого необходимо обратиться к энергетической диаграмме перехода Джозефсона. и возникает нормальная компонента электронов. По какому принципу происходит распад сверхпроводящих носителей заряда?Для этого необходимо обратиться к энергетической диаграмме перехода Джозефсона. В случае, когда 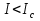 падения напряжения нет и сдвиг между уровнями на диаграмме отсутствует. падения напряжения нет и сдвиг между уровнями на диаграмме отсутствует. В случае, когда 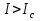 возникает разность потенциалов на ДжК и происходит сдвиг энергетических уровней между двумя сверхпроводящими электродами. Один из электронов куперовской пары туннелирует на нижний(основной) энергетический уровень и в результате чего излучает квант электромагнитной энергии. Выделившейся энергии становится достаточно для разрыва пары. возникает разность потенциалов на ДжК и происходит сдвиг энергетических уровней между двумя сверхпроводящими электродами. Один из электронов куперовской пары туннелирует на нижний(основной) энергетический уровень и в результате чего излучает квант электромагнитной энергии. Выделившейся энергии становится достаточно для разрыва пары.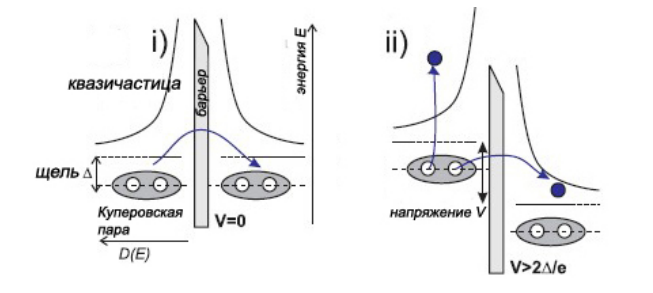 Нелинейная джозефсоновская индуктивность Ток через ДжК : 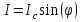 Напряжение на переходе: 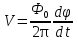 Взяв производную выражения () и используя () получим : 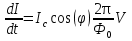 В общем случае 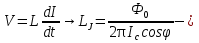 джозефсоновская индуктивность. джозефсоновская индуктивность.Член  показывает, что индуктивность нелинейная. Индуктивность - мера запасенной энергии. Энергию запасенную в переходе можно вычислить: показывает, что индуктивность нелинейная. Индуктивность - мера запасенной энергии. Энергию запасенную в переходе можно вычислить: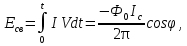 где где 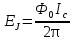 Обобщенная схема джозефсоновского контакта В общем случае ДжК можно представить в виде параллельно соединенного сопротивления, емкости и непосредственно самого дж.перехода(Рис1).  Запишем уравнения для такой системы 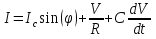 Введем безразмерные величины 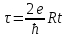 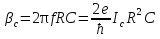 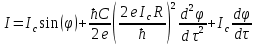 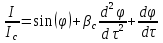 Величина 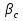 – параметр Маккамбера – параметр МаккамбераУравнение () не решается аналитически. Если 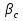 можно пренебречь, то получим : можно пренебречь, то получим :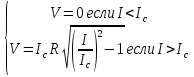  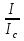 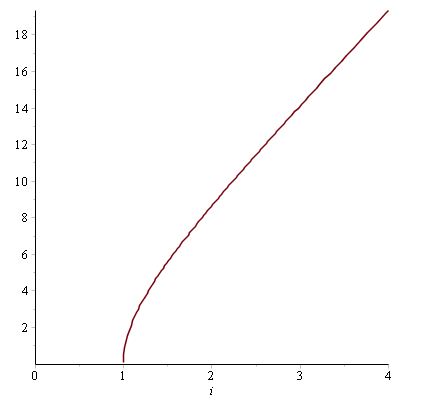 Необходимо дополнить наши выкладки еще одной важной величиной(джозефсоновская частота). Рассмотрим уравнение () и перепишем его в виде: 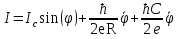 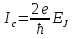 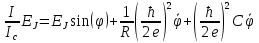 Здесь можно провести аналогию между соотношением () и уравнением движения маятника, где величина 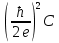 фактически есть момент инерции; фактически есть момент инерции;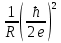 коэффициент вязкости. Таким образом, рассматриваемая нами движущаяся частица обладает свойством инерции, что в дальнейшем сыграет важную роль при рассмотрении ВАХ джозефсоновского перехода. коэффициент вязкости. Таким образом, рассматриваемая нами движущаяся частица обладает свойством инерции, что в дальнейшем сыграет важную роль при рассмотрении ВАХ джозефсоновского перехода.Собственная частота малых колебаний, называемая, в случае рассмотрения джозефсоновского контакта, плазменной частотой перехода и выражается соотношением: 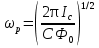 Плазменную частоту можно представить как резонансную частоту джозефсоновского перехода с емкостью С и индуктивностью  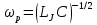 На что влияет параметр Маккамбера и как будет выглядеть ВАХ ДжК при ненулевом значении этого параметра? Во-первых, ненулевое значение параметра Маккамбера указывает на то, что ДжК содержит емкость, на которой возникает переменный ток смещения, следовательно, производная скорости приобретает конечное значение. Поэтому, когда значение тока через переход превысит критическое значение тока, на контакте резко произойдет скачок напряжения. Теперь предположим, что мы увеличиваем ток от нуля до бесконечности(Рис) При достижении критического тока на контакте возникает скачок напряжения и при дальнейшем увеличении тока кривая зависимости выходит на характеристику перехода в нормальном состоянии(ток обеспечивается за счет нормальных электронов). А теперь мы будем уменьшать ток от бесконечности до нуля. Что произойдет? 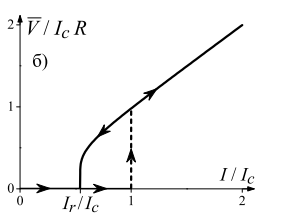 Рисунок ВАХ джозефсоновского перехода при  Поскольку рассматриваемая частица обладает инерцией, то при уменьшении тока до величины критического тока ДжК частица будет обладать конечной скоростью и мгновенного падения напряжения не произойдет! Частица остановится при уменьшении фазы �� т.е. при некотором “токе возврата” 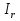 , который по значению меньше критического тока ДжК(Рис). Ток возврата тем меньше, чем выше ёмкость и чем выше сопротивление R т.е. . количественно ток возврата определяется величиной параметра МакКамбера. , который по значению меньше критического тока ДжК(Рис). Ток возврата тем меньше, чем выше ёмкость и чем выше сопротивление R т.е. . количественно ток возврата определяется величиной параметра МакКамбера. 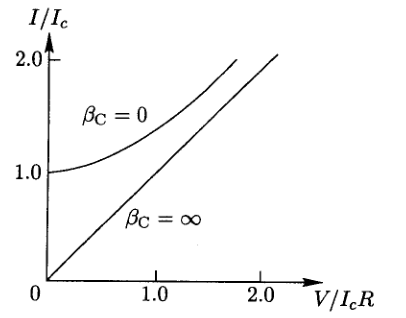 Рисунок ВАХ джозефсоновского контакта при 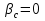 и и 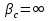 Задача 1 Два джозефсоновских перехода включены параллельно с критическими токами 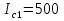 мкА и мкА и 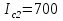 мкА включены параллельно в сверхпроводящую цепь. Полный ток через оба перехода равен 1 мА. Чему равны токи в каждом из переходов? мкА включены параллельно в сверхпроводящую цепь. Полный ток через оба перехода равен 1 мА. Чему равны токи в каждом из переходов? 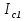 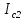 Решение Вследствие того, что ДжК включены параллельно, разности фаз на переходах будут одинаковы. 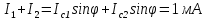 Найдем 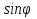 : :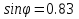 Отсюда 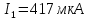 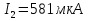 Задача 2 Точечный контакт имеет критический ток 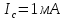 и сопротивление в нормальном состоянии R=2 Ом. Найти величину постоянного напряжения на контакте и сопротивление в нормальном состоянии R=2 Ом. Найти величину постоянного напряжения на контакте 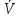 и частоту джозефсоновской генерации υ, если через контакт течет ток I=1.2 мА и частоту джозефсоновской генерации υ, если через контакт течет ток I=1.2 мА Решение В данном случае на ДжК возникает переменное напряжение с частотой 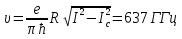 Если мы будем измерять напряжение на переходе вольтметром постоянного тока, то в этом случае мы измерим усредненное по периоду значение 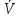 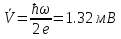 |
