Вариант 3. Для электрической схемы, изображенной на рисунке 18, выполнить следующее

• Название: Для электрической схемы, изображенной на рисунке 18, выполнить следующее
• Дата: 09.02.2022
• Размер: 234.03 Kb.
• Имя файла: Вариант 3.docx
• Тип: Закон; #356662

Вариант 3

Для электрической схемы, изображенной на рисунке 1.18, выполнить следующее:

1. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. Систему не решать.

2. Определить токи во всех ветвях схемы методом контурных токов (МКТ).

3. Определить токи во всех ветвях методом узловых потенциалов (МУП).

4. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой.

5. Составить баланс мощности в схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

Таблица 1 - Исходные данные

№ вар.	Рис.	R1	R2	R3	R4	R5		R6	E1	E2	E3
		Ом					B
3	1.18	18	53	33	10	15		20	-	51	18

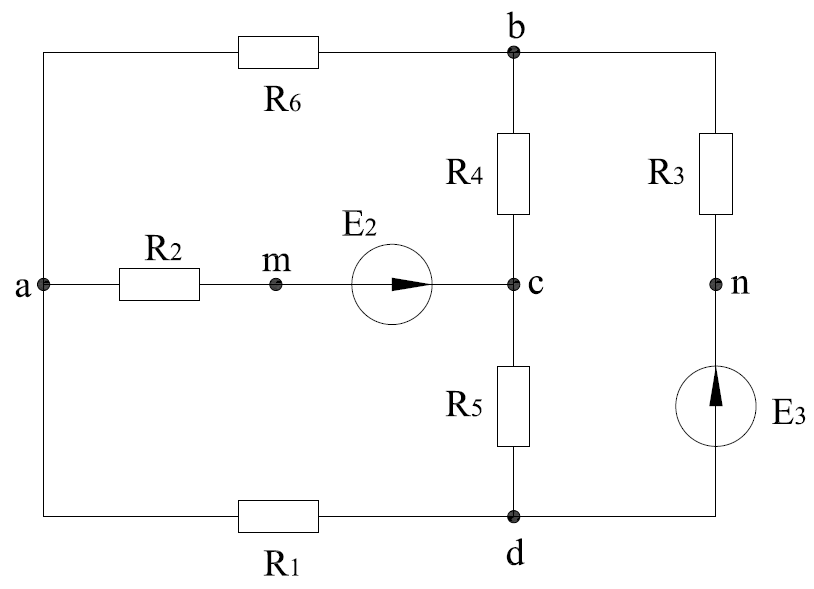Рисунок 1.18 - Схема для расчета
Решение

1. Метод уравнений Кирхгофа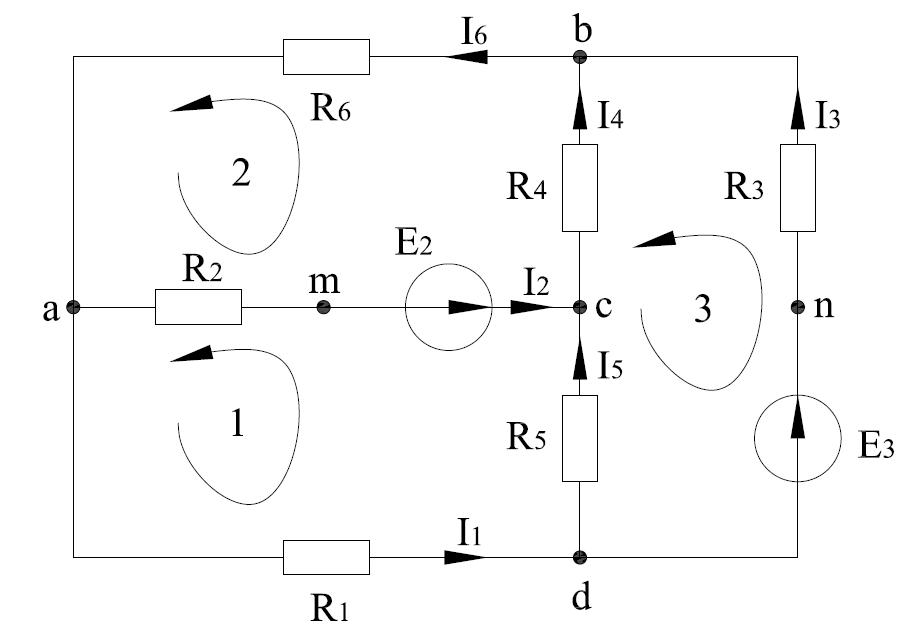



Рисунок 1 - Электрическая схема

В цепи 4 узла, 6 ветвей и 3 независимых контура. По первому закону Кирхгофа составляем n - 1 = n - 1 = 3 (где n - число узлов) уравнений.

Для узла а: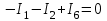

.

Для узла b: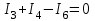

.

Для узла с: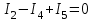

.

Оставшиеся три уравнения составляем по второму закону Кирхгофа, задавшись направлением обхода контуров (выбираем направление обхода контуров против часовой стрелки). Если направление тока в ветви и направление ЭДС совпадают с направлением обхода контура, то

Для первого контура (adcm):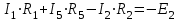

.

Для второго контура (amcb):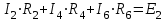

.

Для третьего контура (bcdn):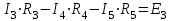

.

Таким образом, получим систему уравнений: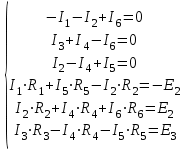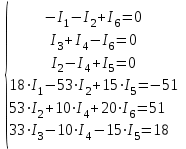

;

.

2. Метод контурных токов

Схема для расчета при помощи метода контурных токов представлена на рисунке 2. Направления контурных токов выбираем произвольно (в данном случае по часовой стрелке).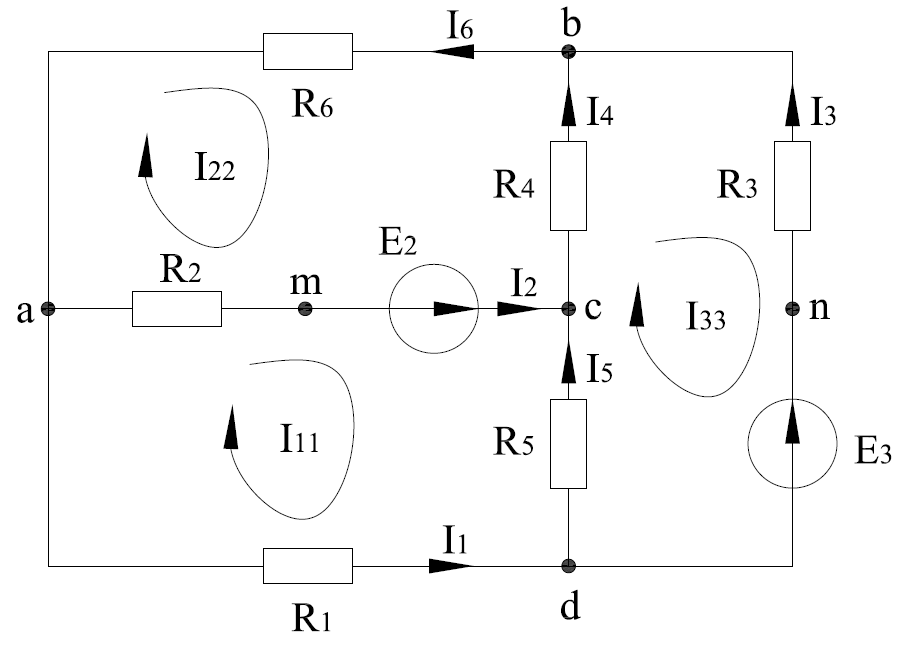



Рисунок 2 - Схема для расчета при помощи метода контурных токов

Для определения контурных токов составляем уравнения по второму закону Кирхгофа: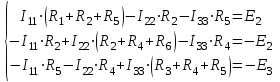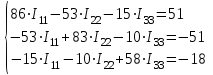

;

.

Решение системы уравнений относительно контурных токов по формулам Крамера:

Главный определитель системы: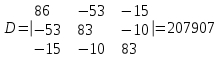

.

Первый вспомогательный определитель: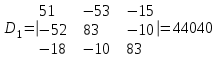

.

Второй вспомогательный определитель: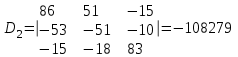

.

Третий вспомогательный определитель: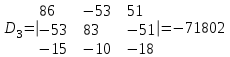

.

Первый контурный ток: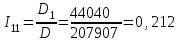

.

Второй контурный ток: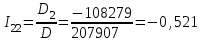

.

Третий контурный ток: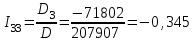

.

Ток в первой ветви схемы:

I₁= -I₁₁ = -0,212 A.

Ток во второй ветви схемы:

I₂ = I₁₁ - I₂₂ = 0,212 - (-0,521) = 0,733 A.

Ток в третьей ветви схемы:

I₃ = - I₃₃ = 0,345 A.

Ток в четвертой ветви схемы:

I₄ = I₃₃ - I₂₂ = -0,345 - (-0,521)= 0,176 A.

Ток в пятой ветви схемы:

I₅ = I₃₃ - I₁₁ = -0,345 - 0,212 = -0,557 A.

Ток в шестой ветви схемы:

I₆ = -I₂₂ = 0,521 A.

3. Метод узловых потенциалов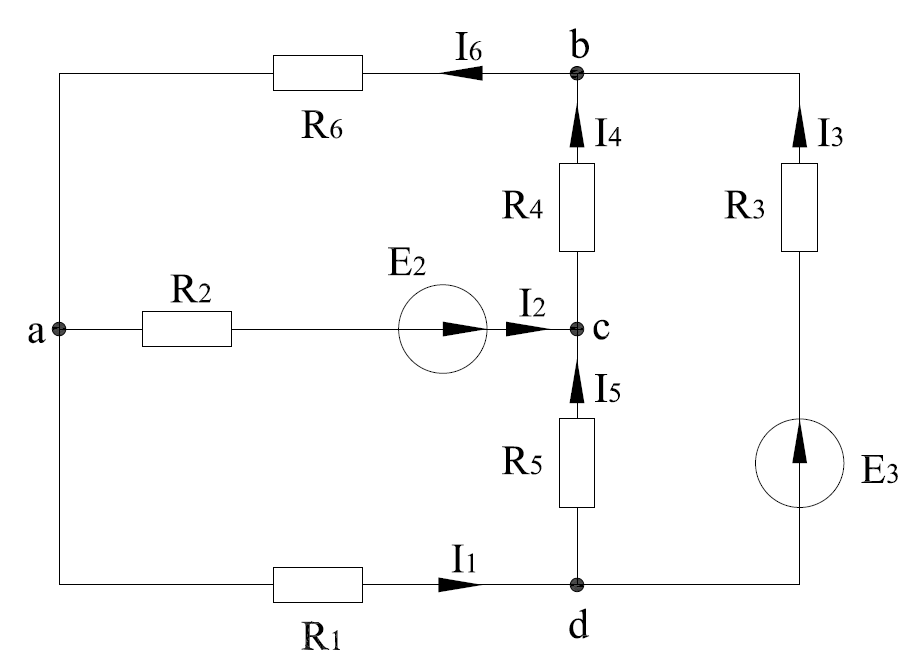



Рисунок 3 - Схема для расчета при помощи метода узловых потенциалов

На схеме на рисунке 3 обозначим базисный узел d, который заземлен и поэтому значение его потенциала известно и равно нулю (0 В), а также оставшиеся три узла a, b и c.

Для узла a: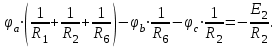



Для узла b: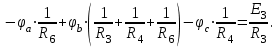



Для узла с: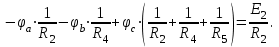



Получим систему уравнений: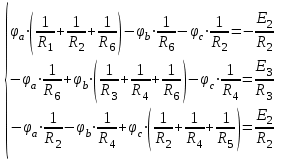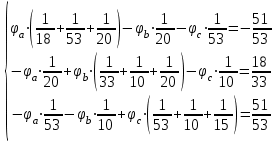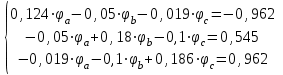

;

;

,

Отсюда _а = -3,825 В; _b = 6,59 В; _с = 8,324 В.

После этого, используя закон Ома для активного участка цепи, определяются все действительные токи ветвей: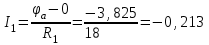

А;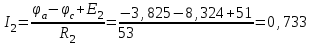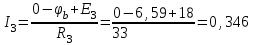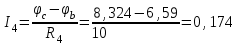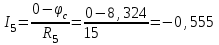

;

А;

А;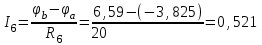

А;

А.

4. Результаты расчета токов, проведенного двумя методами

Таблица 2 - Результаты расчета токов, проведенного двумя методами

Ток	Метод контурных токов	Метод узловых потенциалов	Погрешность
I1, A	-0,212	-0,213	0,47%
I2, A	0,733	0,733	0%
I3, A	0,345	0,346	0,29%
I4, A	0,176	0,174	1%
I5, A	-0,557	-0,555	036%
I6, A	0,521	0,521	0%

Результаты расчетов двумя методами совпадают, значит, расчеты выполнены верно.

5. Баланс мощности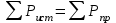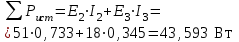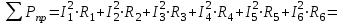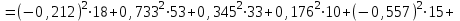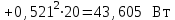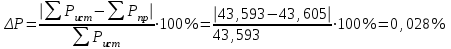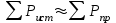

;













Баланс мощностей сошелся.