математика. Для функции (2 3) 5 Найти область определения, точки разрыва

• Название: Для функции (2 3) 5 Найти область определения, точки разрыва
• Анкор: математика
• Дата: 10.04.2022
• Размер: 15.83 Kb.
• Имя файла: математика.docx
• Тип: Документы; #459400

Задание.

Для функции 𝑦 = (2𝑥 + 3)𝑒 5𝑥

1. 
   Найти область определения, точки разрыва.
   
2. 
   Исследовать функцию на четность, периодичность.
   
3. 
   Исследовать поведение функции на концах области определения. Указать асимптоты.
   
4. 
   Найти промежутки монотонности. Точки экстремума.
   
5. 
   Найти промежутки выпуклости. Точки перегиба.
   
6. 
   Найти площадь фигуры, ограниченной графиком функции 𝑦 = (2𝑥 + 3)𝑒 5𝑥 и прямыми 𝑥 = 0, 𝑥 = 2, 𝑦 = 0.
   
7. 
   Результаты исследования оформить в виде таблицы.
   

Область определения:
Четность, периодичность:
Поведение на концах области определения:
Асимптоты:
Промежутки монотонности:
Точки экстремума:
Промежутки выпуклости:
Точки перегиба:
Площадь криволинейной тропеции

1) 𝑦 = (2𝑥 + 3) е^5х

(2𝑥 + 3)𝑒^5𝑥=0

2х+3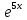=0

=0

Х=- ;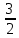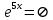

Х= -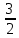

2) y=(2x+3)e^5x

y(-x)=(-2x+3)e^(-5x)

y(-x) не равно y(x)

y(-x) не равно -y(x)

Функция не является ни чётной, ни нечётной. Функция не является периодической.

3)