Для необратимой реакции нулевого порядка, когда

• Название: Для необратимой реакции нулевого порядка, когда
• Дата: 26.12.2020
• Размер: 86.41 Kb.
• Имя файла: bryankin-pages-deleted-edited-converted.docx
• Тип: Документы; #164567

^ХА dХ 1 ^{Х А}dХ

или

τ  С_{А,0 }^А  _{ }^А . (2.8)

kС

kС
п

0 ^А,0

1 Х

_Ап

п 1

А,0 ₀

1 Х

_{А }п

Для необратимой реакции нулевого порядка, когда п = 0, из уравнения (2.8) получаем

1 ^ХА dХ ^{С Х}


kС
τ  _^А ^А,0А. (2.9)

01

А,0

₀ 1 Х

_А0 _k

Для необратимой реакции первого порядка, когда п = 1, аналогично из уравнения (2.8) находим

1 ^{Х А}dХ

 d1 Х  1 ^ 1 ^

τ  <sub>

</sub>А _А_

ln<sup>

</sup> . (2.10)

kС
1 1

А,0

₀ 1 Х _А

1 Х _А

k _ 1 Х _{А }

До сих пор интегрирование производилось в пределах изменения Х_Аот 0 до Х_А. Если начальная степень превращения не равна 0, тогда во всех случаях конечные результаты изменяются. Так, например, для реакции нулевого порядка из уравнения (2.8) имеем

1 ^{Х А}

dХ_А

^СА,0 _{ }

^{τп0 } _kС 01

^ 1 Х

_0  _k

Х _А  Х _А,0 .

^{А,0 Х}А,0 ^А

Соответственно для реакции первого порядка

^{1 ХА dХ 1} Х

^τп1 ^ _{ }



^А  

ln1 Х _А  ^А

или

11

А,0 _{Х А,0}

1 Х_А k

^Х А,0

τ  ¹ ln ^{1 Х А,0} .

п1 _k

1 Х _А

В тех случаях, когда в РИС-П проводится реакция, порядок которой отличается от 0 и 1 (0 ≠ п ≠ 1) интег- рирование уравнения (2.6) связано с трудностями, поэтому определение рабочего времени производят методом графического интегрирования. Для этого, взяв за основу уравнение (2.6), строят графическую зависимость

1

• 
  r_A
  

 f Х

_А  и вычисляют площадь под кривой между начальным и конечным значениями степени превраще-

ния (рис. 2.3):

где

Х_А

S  _

0
1

• 
  r_A
  

dХ _А  _С
τ

А,0

Х_А

τ  С_{А,0 }

0

. (2.12)

1

• 
  r_A
  

dХ _А  С_А,0S, (2.11)

1

• 
  r_A
  

Х_А

Рис. 2.3. Графический метод расчета РИСП

Уравнение (2.6) является математическим описанием модели РИС-П. Исходя из этого уравнения представ- ляется возможность определить размеры реактора, а также исследовать эту модель с точки зрения нахождения оптимальных значений всех входящих в него параметров.

Реакторы периодического действия просты по конструкции, требуют небольшого числа вспомогательного оборудования, поэтому они особенно удобны для проведения опытных работ по изучению химической кинети- ки. В промышленности они обычно используются в малотоннажных производствах и для переработки относи- тельно дорогостоящих химических продуктов. Большинство же промышленных процессов оформляется с исполь- зованием реакторов непрерывного действия.

2. РЕАКТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ

В реакторах непрерывного действия (или проточных реакторах) питание реагентами и отвод продуктов реакции осуществляется непрерывно.

Если в периодическом реакторе можно непосредственно, по часам, измерить продолжительность реакции, то в реакторе непрерывного действия этого сделать нельзя, так как при установившемся режиме в этих реакто- рах параметры не меняются со временем. В связи с этим для непрерывных реакторов применяют понятие ус- ловного времени пребывания реагентов в системе (времени контакта)

τ  V_rV₀ , (2.13)

где V_r– объем реактора; V₀ – объем реакционной смеси, поступающей в реактор в единицу времени (объемный расход реагентов).

1. Реакторы идеального вытеснения

Реактор идеального вытеснения (РИВ) представляет собой трубчатый аппарат, в котором отношение дли- ны трубы L к ее диаметру d достаточно велико. В реактор непрерывно подаются исходные реагенты, которые превращаются в продукты реакции по мере перемещения их по длине реактора (рис. 2.4).

Гидродинамический режим в РИВ характеризуется тем, что любая частица потока движется только в од- ном направлении по длине реактора, обратное (продольное) перемешивание отсутствует; отсутствует также перемешивание по сечению реактора. Предполагается, что распределение вещества по этому сечению равно- мерное, т.е. значения параметров реакционной смеси одинаковые.

Каждый элемент объема реакционной массы dV_rдвижется по длине реактора, не смешиваясь с предыду- щими и последующими элементами объема, и ведет себя как поршень в цилиндре, вытесняя все, что находится перед ним. Поэтому такой режим движения реагентов называется иногда поршневым или режимом полного вытеснения.

Состав каждого элемента объема последовательно изменяется по длине реактора вследствие протекания химической реакции. Концентрация исходного реагента А постепенно меняется по длине реактора от начально- го значения C_А,0 до конечного С_А(рис. 2.4). Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же.

При составлении математического описания РИВ исходят из дифференциального уравнения материального баланса, преобразуя его с учетом указанных выше особенностей этого реактора.

dV

Х Х_А

⁰ L l

Рис. 2.4. Реактор идеального вытеснения и зависимости концентрации реагента С_Аи степени превращения Х_Аот длины реактора
Поскольку в РИВ реакционная смесь движется только в одном направлении (по длине l), то

 w ^CA  0;

 w ^CA  0 ;  w

C_{A  w} C_{A ,}

^у у

^z z

^х х l

где w – линейная скорость движения реакционной смеси в реакторе;l – длина (длина пути, пройденного эле- ментом объема реакционной смеси в реакторе).

Так как в идеальном реакторе каждый элемент объема реакционной смеси не смешивается ни с предыду- щими, ни с последующими объемами, а также отсутствует радиальное перемешивание (нет ни продольной, ни ради- альной диффузии, а молекулярная диффузия мала), то

_D


^  ²C<sub>A

</sub>  ²C_{A }


2 _


 C_A


^  0 .

^ x²

y²

z ^{2 }

С учетом вышесказанного, уравнение (1.7) для реактора идеального вытеснения принимает вид

^CA  w ^CA  r


. (2.14)

τ l ^A

Это уравнение материального баланса является математическим описанием потока реагента в реакторе идеального вытеснения при нестационарном режиме (когда параметры процесса не только меняются по длине реактора, но и непостоянны во времени). Подобный режим характерен для периодов пуска и остановки реакто- ра. Член дС_А/дτ характеризует изменение концентрации А во времени для данной точки реактора, т.е. накопле- ние вещества А в этой точке.

Стационарный режим характеризуется тем, что параметры в каждой точке реакционного объема не меня- ются во времени (дС_А/дх = 0). В этом случае уравнение (2.14) принимает вид

w ^dCA  r


. (2.15)

Если объем реакционной смеси не меняется в процессе, то

dC_A  С_А,0dХ _А .

Но в любой момент времени х имеем dl dτ  w или dl  wdτ .

dl ^A

Подставив полученное значение для dC_Aи dl в уравнение (2.15), находим

dτ  С ^dХА. (2.16)


A
А,0 _{ r}

После интегрирования уравнения (2.16) в пределах изменения степени превращения от 0 до Х_Аполучаем


dХ
Х _А

τ  С_{А,0 }^А. (2.17)

₀  r_A

Из полученных данных видно, что уравнение для РИВ в общем виде такое же, как и для РИС-П [уравнения (2.8) – (2.10)], поэтому для РИВ при различных значениях п можно записать

1 ^{Х А}dХ

^τпп ^

_^А ; (2.18)

kС
п1 А,0

₀ 1 Х _А 

п

τ  ^{СА,0 ХА}; (2.19)

^τп1

п0
 ¹ ln

k

k

1

1 Х_А

. (2.20)

Для реакций, порядок которых отличен от нуля и единицы, пользуются графическим методом, который опи- сан применительно к РИС-П. При этом

где


Х_А

S  _

0


1

• 
  r_A
  

dХ _А  _С


τ

А,0

Х_А

^{τ  С}А,0 _

0
. (2.22)

1

• 
  r_A
  

dХ _А  С_А,0S, (2.21)

В уравнениях для РИС-П величина τ – время проведения реакции от загрузки исходного реагента до вы- грузки продуктов реакции, а в уравнениях для РИВ τ – время, в течение которого реакционная смесь проходит через РИВ от входа в реактор до выхода из него.

Если в процессе реакции происходит изменение объема реакционной смеси, то в уравнения (2.16) и (2.17)

необходимо подставить значение скорости реакции с учетом изменения объема реакционной смеси

^ 1  Х ^п

• 
  
  А
  
  А 
  r_A  kС^{пА}
  

. (2.23)

где

ε _А – относительное изменение объема системы. Тогда уравнение РИВ запишется в виде

^А _ 1 ε Х

1 ^{Х А} 1 ε Х^п


kС
τ  _^{А А} dХ_А. (2.24)

п1 А,0 ₀

1 Х

_{А }п

В реальном реакторе гидродинамическая обстановка отличается от обстановки в идеальном реакторе. На- пример, в реальном реакторе вытеснения, помимо поршневого движения основного потока по длине реактора, возможно перемешивание потока в продольном и радиальном направлениях. Естественно, модель реактора ус- ложняется. При наличии продольного перемешивания (по оси х) уравнение реактора вытеснения имеет вид

где D_L – коэффициент продольного перемешивания.

^CA  w

τ

C_A

l

• 
  D_L
  

 ²C_A

 ²l

 r_A, (2.25)

Модель трубчатого реактора называется диффузионной однопараметрической моделью, так как ею учиты- вается один диффузионный параметр – продольное перемешивание.

Степень отклонения показателей реального реактора от идеального зависит от трех величин: коэффициен- та продольного перемешивания (конвективной диффузии) D_L, линейной скорости потока w и длины реактора l. Эти величины сведены в безразмерный комплекс D_L/(wL). Степень отклонения показателей такого реактора от показателей РИВ зависит от значения этого комплекса и может быть выражена через соотношение объемов реального V_p и идеального реакторов V_ид, необходимых для достижения одинаковой степени превращения Х_А(рис. 2.5).

Если

^DL  0 , наблюдается режим идеального вытеснения; в этом случае V /V


= 1, а зависимость V /V

_wL р ид

р ид

от Х изображается в виде прямой, параллельной оси абсцисс (рис. 2.5). Если

^DL > 0, то V /V

> 1; при этом с

А
увеличением Х_Аотношение в V_р/V_ид возрастает.

_wL р ид

Таким образом, отношение V /V

зависит от комплекса

^DL и Х


и в общем виде выражается в виде урав-

нения

р ид

wL ^А
V_р ^Vид


 f ^{ DL} , X

_ wL
^ . (2.26)


_A 


Чем выше

^DL , т.е. чем больше отклонение гидродинамического режима в реальном реакторе от режима в

wL

идеальном реакторе, тем

^Vр  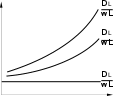

^Vид

 1

₁  0
X_A

Рис. 2.5. Зависимость отношения объема реального реактора вытеснения к объему реактора идеального вытеснения V_р/V_ид от степени превращения Х_Аи от D_L/wL

необходим больший объем реального реактора, и эта разница возрастает с увеличением значения Х_А.

При учете не только продольного, но и радиального перемешивания в реакторе

^CA  w

τ

C_A

l

• 
  D_L
  

 ²C_A

l ²

• 
  D_R
  

 ²C_A

R²

 r_A, (2.27)

где D_R– коэффициент радиального перемешивания; R – радиус трубы реактора.

Такую модель называют двухпараметрической диффузионной моделью, так как она учитывает два диффу- зионных параметра – продольное и радиальное перемешивание.

2. Реактор идеального смешения непрерывный

Реактор идеального смешения непрерывный (РИС-Н) представляет собой аппарат с мешалкой, в который не- прерывно подаются реагенты, и также непрерывно выводятся из него продукты реакции (рис. 2.6).

В РИС-Н наблюдается резкое изменение концентрации исходного реагента при входе в реактор в результате мгновенного смешения поступающей смеси с реакционной массой, уже находящейся в реакторе, где кон- центрация исходного реагента значительно ниже, чем концентрация исходного реагента в поступающей смеси (рис. 2.7).

Точка, соответствующая входу реагентов в реактор, нанесена на ось абсцисс правее начала координат, что дает более наглядное представление об изменении концентрации исходного вещества при входе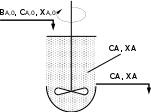

Рис. 2.6. Реактор идеального смешения непрерывный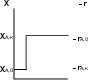

^у0 у у₀

у у₀ у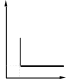

а) б) в)

Рис. 2.7. Изменение параметров процесса в РИС-Н:

а – концентрация реагента С_А; б – степень превращения Х_А; в – скорость реакции r_А
реакционной смеси в реактор. Благодаря тому, что в РИС-Н реакционная смесь мгновенно перемешивается, во всем объеме реактора одинакова концентрация исходного реагента, и она тем ниже, чем больше время пребы- вания реагентов в реакторе. По этой же причине по всему объему реактора одинакова и степень превращения и скорость реакции. Таким образом, для РИС-Н характерным является отсутствие градиента параметров как во времени, так и в объеме реактора, поэтому уравнение материального баланса составляют сразу для реактора в целом. При этом градиенты параметров в дифференциальной форме заменяются разностью значений парамет- ров на входе в реактор и на выходе из него:

^ВА (х.р) ^=ВА(конв) ^{. (2.28)}

Но В_А(х.р) = (–r_A)V_rи В_А(конв)=V(С_А,0 – С_А), подставив их в уравнение (2.28), находим

τ  ^{СА,0  СА}  ^{СА,0 ХА}. (2.29)

• 
  r_А  r_А
  

Для простой необратимой реакции п-го порядка уравнение (2.29) принимает вид

kС
_{τ } ^СА,0 ^{Х А}_


^СА,0 ^ХА _ ^Х_А

А,0

; (2.30)

kС
для реакции нулевого порядка

пп

п А,0

п А,0

1  Х

_{А }п

kС^п11  Х

_{А }п