|
стат. 400.стат.. Для расчёта показателей приведём сводную таблицу Диапазон цен,руб
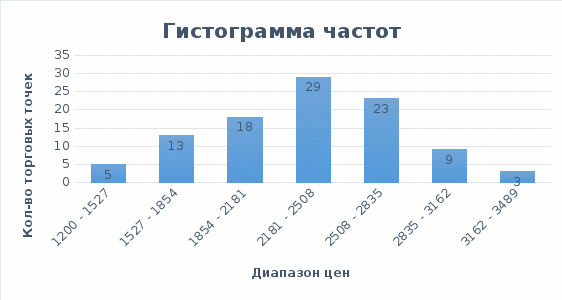
Для расчёта показателей приведём сводную таблицу
Диапазон цен,руб.
|
Середина интервала, xцентр
|
Кол-во, fi
|
xi·fi
|
|x-xср|·fi
|
(x-xср)2·fi
|
1200 - 1527
|
1363.5
|
5
|
6817.5
|
4757.85
|
4527427.325
|
1527 - 1854
|
1690.5
|
13
|
21976.5
|
8119.41
|
5071139.904
|
1854 - 2181
|
2017.5
|
18
|
36315
|
5356.26
|
1593862.288
|
2181 - 2508
|
2344.5
|
29
|
67990.5
|
853.47
|
25117.622
|
2508 - 2835
|
2671.5
|
23
|
61444.5
|
8197.89
|
2921973.933
|
2835 - 3162
|
2998.5
|
9
|
26986.5
|
6150.87
|
4203689.084
|
3162 - 3489
|
3325.5
|
3
|
9976.5
|
3031.29
|
3062906.355
|
Итого
|
|
100
|
231507
|
36467.04
|
21406116.51
|
Средняя стоимость букета
Дисперсия
=
Среднее квадратическое отклонение
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
Составим таблицу
xi-xi+1
|
fi
|
x1 = (xi - xср)/s
|
x2 = (xi+1 - xср)/s
|
Ф(x1)
|
Ф(x2)
|
pi=Ф(x2)-Ф(x1)
|
Ожидаемая частота, 100*pi
|
Эмпирическое значение К
|
1200 - 1527
|
5
|
-2.398
|
-1.6948
|
-0.4918
|
-0.4554
|
0.0364
|
3.64
|
0.5081
|
1527 - 1854
|
13
|
-1.6948
|
-0.9916
|
-0.4554
|
-0.3413
|
0.1141
|
11.41
|
0.2216
|
1854 - 2181
|
18
|
-0.9916
|
-0.2883
|
-0.3413
|
-0.1141
|
0.2272
|
22.72
|
0.9806
|
2181 - 2508
|
29
|
-0.2883
|
0.4149
|
-0.1141
|
0.1628
|
0.2769
|
27.69
|
0.06198
|
2508 - 2835
|
23
|
0.4149
|
1.1181
|
0.1628
|
0.3686
|
0.2058
|
20.58
|
0.2846
|
2835 - 3162
|
9
|
1.1181
|
1.8214
|
0.3686
|
0.4664
|
0.0978
|
9.78
|
0.06221
|
3162 - 3489
|
3
|
1.8214
|
2.5246
|
0.4664
|
0.4945
|
0.0281
|
2.81
|
0.01285
|
|
|
|
|
|
|
|
|
2.1319
|
Kkp = χ2(7-2-1;0.05) = 9.48773; Kнабл = 2.13
Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Данные выборки имеют нормальное распределение.
Выдвигаем нулевую гипотезу H0 о том, что значение математического ожидания генеральной совокупности μ0: = 2400.
Эксперементальное занчение =
По таблице Стьюдента находим:
Tтабл(n-1;α/2) = Tтабл(20;0.0125) = 2.423
tkp = (-∞ ;-2.423)U(2.423; +∞)
T < tkp, поэтому нулевую гипотезу следует принять, на уровне значимости 2,5% можно утверждать, что средняя стоимость букета равна 2400 руб. |
|
|
 Скачать 20.19 Kb.
Скачать 20.19 Kb.
