Для того, чтобы проверить, является ли векторное поле потенциальным, необходимо проверить выполнение равенства
 Скачать 1.27 Mb.
|
 Для того, чтобы проверить, является ли векторное поле потенциальным, необходимо проверить выполнение равенства 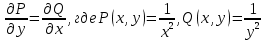 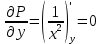 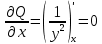 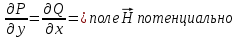 Для нахождения уравнения векторных линий решим дифференциальное уравнение 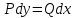  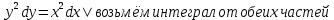  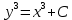 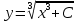  Найдём потенциал поля при помощи криволинейного интеграла 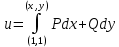 Выбираем начальную точку (1,1), так как функции P и Q в ней существуют, а также она удобна для вычислений: 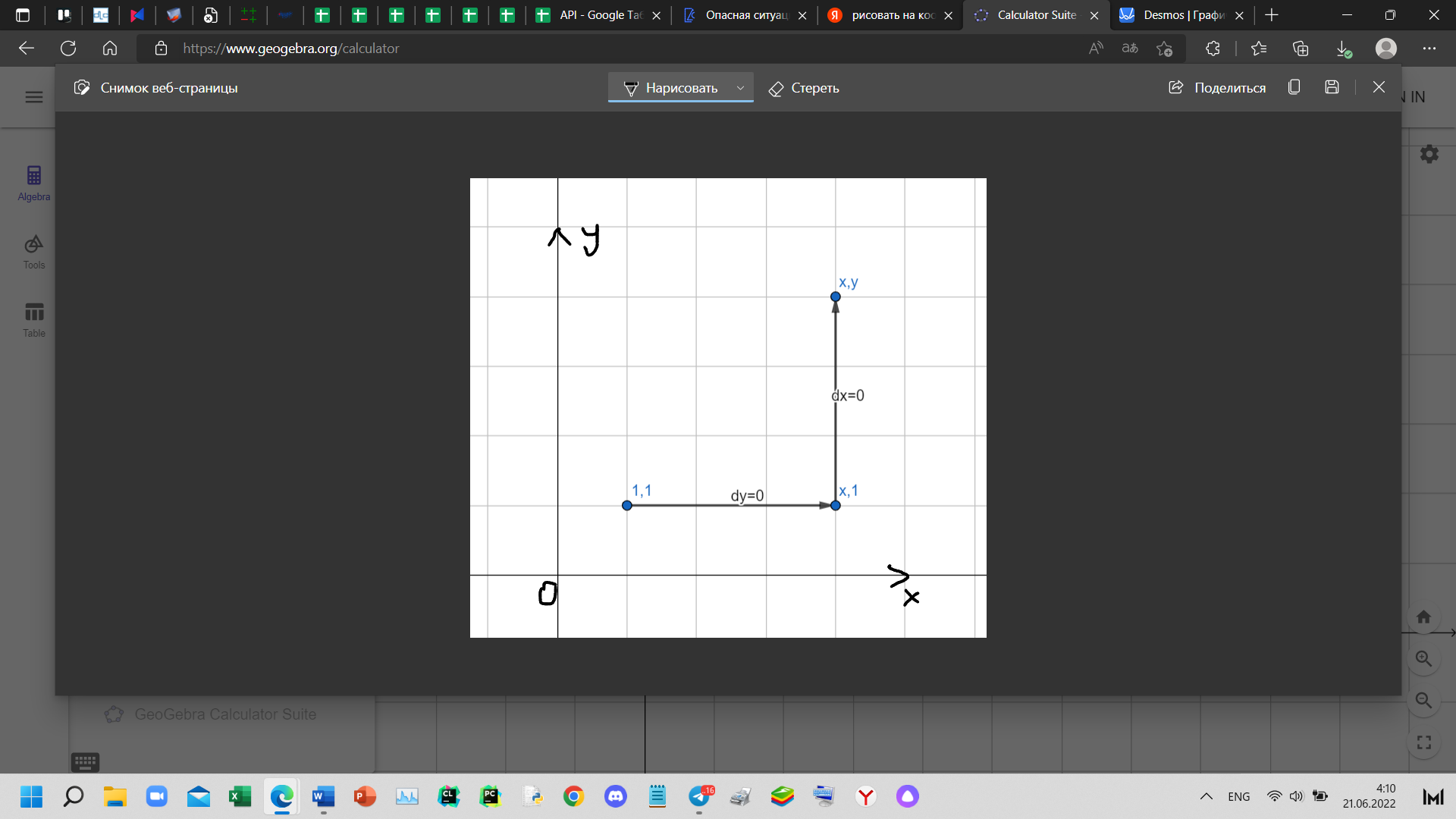 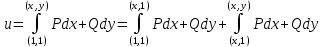 Учитывая выбранный путь, подставим в необходимые места dy=0 и dx=0:   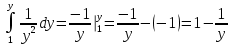  Найдём уравнения линий уровня потенциала: 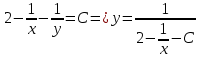  Докажем ортогональность векторных линий поля и эквипотенциальных линий  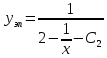  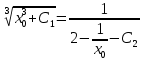 Найдём уравнение нормали для функции Найдём производную функции:   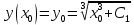 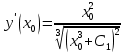 Найдём уравнение нормали к графику в точке     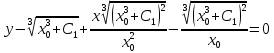 Найдём уравнение нормали для функции 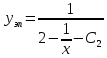Найдём производную функции:   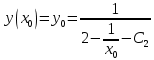 Найдём уравнение нормали к графику в точке   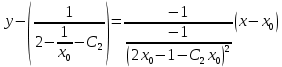 Вычислим работу поля вдоль векторной линии 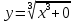 от точки  до точки  Используя результат из пункта 3), получим: 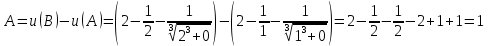 |