Степан Шахов. Решение по данному начальному условию (решим задачу Коши)
 Скачать 178.85 Kb. Скачать 178.85 Kb.
|
|
Задача 1. Найти общее решение дифференциального уравнения. 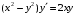 Разделим обе части уравнения на 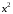 : : 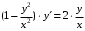 . . Полученное уравнение есть однородное дифференциальное уравнение 1 порядка. Сделаем замену: 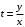 , , 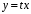 , , 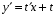 . .Получим 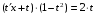 ; ; 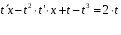 ; ; 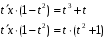 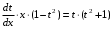 Разделим переменные 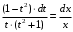 . Интегрируем обе части равенства 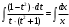 Разложим дробь 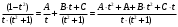 Приравниваем коэффициенты при одинаковых степенях t,получаем систему уравнений 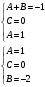 Получаем 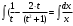 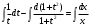 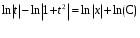 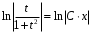 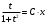 Выполним обратную замену 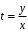 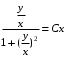 . .Получено общее решение данного уравнения Ответ 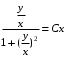 Задача 2. Найти частное решение дифференциального уравнения 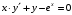 , удовлетворяющего начальному условию , удовлетворяющего начальному условию 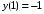 . .Решение. Разделим обе части уравнения на  : : 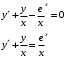 . . Полученное уравнение есть линейное дифференциальное уравнение 1 порядка. Сделаем замену: , 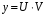 , , 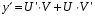 . .Получим 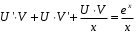 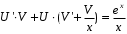 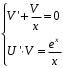 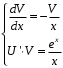 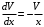 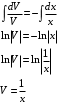 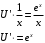 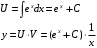 Получено общее решение данного уравнения. Найдем частное решение по данному начальному условию (решим задачу Коши). При 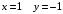 имеем имеем 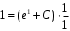 , , 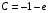 . . Таким образом 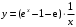 . .Ответ 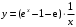 2 cпособ решения Разделим обе части уравнения на  : : 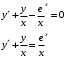 Метод Лагранжа. Пусть 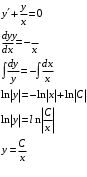 Пусть C=C(x) 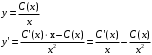 Подставляем в исходное 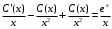 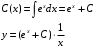 Получено общее решение данного уравнения. Найдем частное решение по данному начальному условию (решим задачу Коши). При 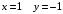 имеем имеем 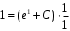 , , 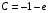 . . Таким образом 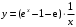 . .Ответ 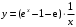 Задача 3. Найти частное решение дифференциального уравнения 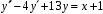 , удовлетворяющее начальным условиям , удовлетворяющее начальным условиям 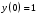 , ,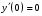 двумя способами: двумя способами:классическим и 2) операционным. Решение классическим методом. Данное уравнение - линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его решение находим в виде: 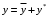 , где , где 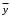 - общее решение соответствующего однородного уравнения - общее решение соответствующего однородного уравнения 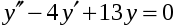 , , 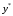 - какое-либо частное решение исходного уравнения. - какое-либо частное решение исходного уравнения. Решим соответствующее однородное уравнение. Составим характеристическое уравнение и найдем его корни: 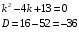 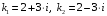 Итак, данное уравнение имеет два различных действительных корня. Общее решение однородного уравнения имеет вид: 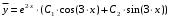 , где , где 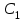 и и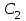 произвольные постоянные. произвольные постоянные.Так как правая часть уравнения совпадает с одним из базисных решений, то частное решение нашего уравнения следует искать в виде: 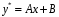 Найдем неопределенный коэффициент А. Для этого подставим 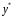 в исходное уравнение: в исходное уравнение: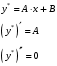 . .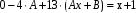 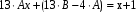 . 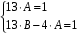 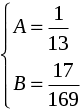 Следовательно, 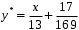 и общее решение данного уравнения примет вид: 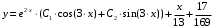 Найдем теперь частное решение, используя начальные условия. Заметим, что 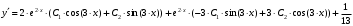 Имеем 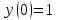 и и 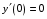 . Тогда . Тогда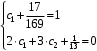 ИЛИ ИЛИ 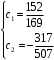 Получаем: 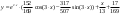 ОТВЕТ: 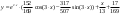 Решение операционным методом. Найдем изображение исходного уравнения. Обозначим изображение искомой функции Y(p), т.е. 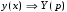 Используя теорему о дифференцирования оригинала, получим: 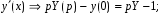 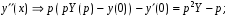 Изображение правой части 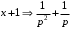 Изображение уравнения примет вид 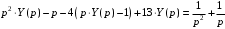 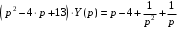 Выразим Y(p) : 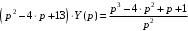 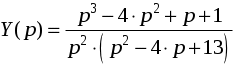 Для восстановления оригинала разложим дробь на простейшие дроби 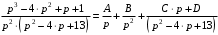 Применим метод неопределенных коэффициентов для нахождения А,В и С: 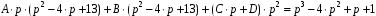 Получим 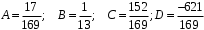 Окончательно: 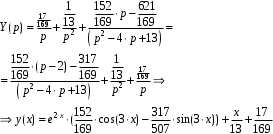 ОТВЕТ 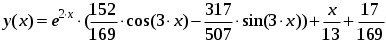 |
