GPSS Червяков И.С. 61-20. Длявыполненияработ поразделу 2 (ИМ) в системе gpss
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Вариант 3.2.2.Нарисовать схему СМО, содержащую одноканальное устройство (ОКУ), на вход которого поступает поток заявок, загружающий ОКУ на 80%, а после обслуживания в ОКУ этот поток делится на 5 направлений с заданными вероятностями соответственно 0.1, 0.2, 0.3, 0.15 и 0.25. С вновьобразованнымипотоками происходит следующее: Первый поток поступает на вход ОКУ, образуя свою очередь заявок с приоритетом на1 меньше, чем заявки первоначального входного потока. Остальные 4 потока распределяются на различные схемы, построенные по вашему усмотрению… Запустить программу и по результатам экспериментов с моделью определить погрешность в оценке распределения первоначального потока с заданными вероятностями… 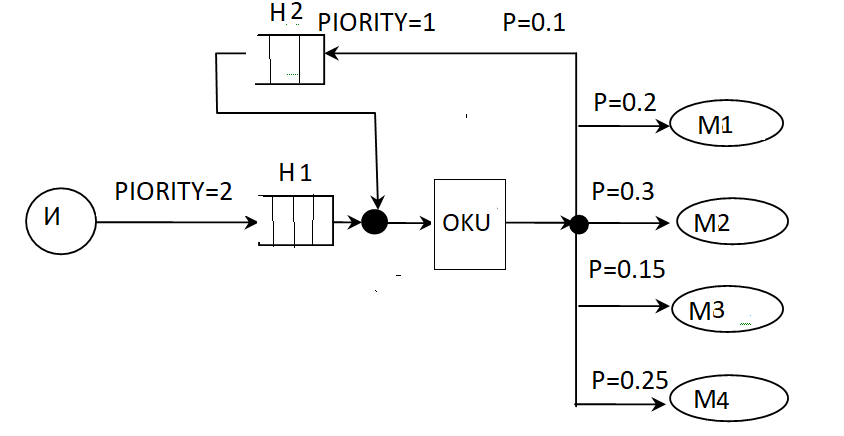 Программа GPSS Generate 10,1 PRIORITY 2 QUEUE OCH1 Seize OKU DEPART OCH1 ADVANCE 7,1 Release OKU Met5 SaveValue NPP+,1; подсчет выходного потока из OKU Transfer .9,Met0,Met; Разделение выходного потока OKU на 4 потоука Met0 PRIORITY 1; Уменьшение приоритета на 1 лдя обратной ветви потока SaveValue NP1+,1; подсчёт числа заявок, пошедших по обратной ветви QUEUE OCH2; очередь для повторной обработки заявок подпотока с вер. 0.1 Seize OKU DEPART OCH2 ADVANCE 7,1 Release OKU Transfer ,Met5; Переход на метку разделения потока Met Transfer .778,Met2,Met32 Met2 SaveValue NP2+,1; метка блока для части вых потока заявок с вероятностью 0.2 Terminate Met32 Transfer .571,Met3,Met45 Met3 SaveValue NP3+,1; метка блока для части вых потока заявок с вероятностью 0.3 Terminate Met45 Transfer .625,Met4,Met6 Met4 SaveValue NP4+,1; метка блока для части вых. потока заявок с вероятностью 0.15 Terminate Met6 SaveValue NP5+,1; метка блока для части вых. потока заявок с вероятностью 0.25 Terminate Generate 10000; время моделирования Terminate 1 Start 1 Результаты моделирования GPSS World Simulation Report - M_3_2_2.5.1 Thursday, May 26, 2022 11:53:05 START TIME END TIME BLOCKS FACILITIES STORAGES 0.000 10000.000 30 1 0 NAME VALUE MET 18.000 MET0 10.000 MET2 19.000 MET3 22.000 MET32 21.000 MET4 25.000 MET45 24.000 MET5 8.000 MET6 27.000 NP1 10007.000 NP2 10005.000 NP3 10003.000 NP4 10006.000 NP5 10004.000 NPP 10002.000 OCH1 10000.000 OCH2 10008.000 OKU 10001.000 LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY 1 GENERATE 998 0 0 2 PRIORITY 998 0 0 3 QUEUE 998 0 0 4 SEIZE 998 0 0 5 DEPART 998 0 0 6 ADVANCE 998 0 0 7 RELEASE 998 0 0 MET5 8 SAVEVALUE 1107 0 0 9 TRANSFER 1107 0 0 MET0 10 PRIORITY 109 0 0 11 SAVEVALUE 109 0 0 12 QUEUE 109 0 0 13 SEIZE 109 0 0 14 DEPART 109 0 0 15 ADVANCE 109 0 0 16 RELEASE 109 0 0 17 TRANSFER 109 0 0 MET 18 TRANSFER 998 0 0 MET2 19 SAVEVALUE 224 0 0 20 TERMINATE 224 0 0 MET32 21 TRANSFER 774 0 0 MET3 22 SAVEVALUE 327 0 0 23 TERMINATE 327 0 0 MET45 24 TRANSFER 447 0 0 MET4 25 SAVEVALUE 186 0 0 26 TERMINATE 186 0 0 MET6 27 SAVEVALUE 261 0 0 28 TERMINATE 261 0 0 29 GENERATE 1 0 0 30 TERMINATE 1 0 0 FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY OKU 1107 0.776 7.010 1 0 0 0 0 0 QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY OCH1 1 0 998 775 0.067 0.669 2.996 0 OCH2 3 0 109 81 0.048 4.425 17.228 0 SAVEVALUE RETRY VALUE NPP 0 1107.000 NP3 0 327.000 NP5 0 261.000 NP2 0 224.000 NP4 0 186.000 NP1 0 109.000 FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE 1000 0 10002.675 1000 0 1 1001 0 20000.000 1001 0 29 Среднее время моделирования составило 10000 мин. Заявки порождались на 1 входе со средним интервалом 10 мин и обрабатывались на устройстве в среднем за 7 мин одна заявка. Было создано 998 заявок Прошло обработку на OKU и было выделено из выходного потока OKU NP2+NP3+NP4+NP5=224+327+186+261=998 заявок, из них на дообработку по обратной связи направлялось NP1=109 заявок. На устройство было подано и обработано 1107 заявок, коэффициент использования составил 0.776. Статистические вероятности разделения потока на 5 подпотоков равны p1s=NP1/Npp=109/1107=0.098464 при теоретической вероятности p1=0.9, p2s=NP2/NPP=224/1107=0.2023(p2=0.2), p3s=NP3/NPP=327/1107=0.2954(p3=0.3), p4s=NP4/NPP=186/1107=0.1680(p4=0.15),p5s=NP5/NPP=261/1107=0.2358(p5=0.25), таким образом, статистические вероятности равны теоретическим. Вариант 3.2.3. Предыдущие варианты можно выполнить , заменив блокTRANSFER на блок FUNCTION. Решение. Решим пункт 3.2.2 используя блок FUNCTION Программа имеет вид perecl function RN5,D5 0.1,Lb1/0.3,Lb2/0.6,Lb3/0.75,Lb4/1,Lb5 Generate 11,1 PRIORITY 2 QUEUE OCH1 Seize OKU1 DEPART OCH1 ADVANCE 8,1 Release OKU1 Met0 Transfer , fn$perecl Lb1 PRIORITY 1 QUEUE OCH2; очередь для повторной обработки заявок подпотока с вер. 0.1 Seize OKU1 DEPART OCH2 ADVANCE 8,1 Release OKU1 Transfer ,Me0 Lb2 Terminate; метка блока для части вых потока заявок с вероятностью 0.2 Lb3 Terminate; метка блока для части вых потока заявок с вероятностью 0.3 Lb4 Terminate; метка блока для части вых. потока заявок с вероятностью 0.15 Lb5 Terminate; метка блока для части вых. потока заявок с вероятностью 0.25 Generate 10000; время моделирования Terminate 1 Start 1 Результаты соответствуют п.3.2.2 4. ЗАДАНИЕ на тему: сравнение результатов математического и имитационного моделирования на примерах моделирования АвтоЗаправочных Станций (АЗС). 24: ЗАДАНИЯ НА САМОСТОЯТЕЛЬНУЮ РАБОТУ (2 в 1:ММ и ИМ) Выбрать одно из 24 вариантов типовых заданий, представленных таблицами, и выполнить двумя способами - аналитическим расчётом и имитационным моделированием в системе GPSS и сравнить результаты моделирования. Система обслуживания (СМО) представляет собой автозаправку (АЗ) с N бензоколонками (БК), к которой подъезжают автомобили (АМ) с частотой LАМ в минуту и, если нет очереди, то сразу подъезжают к одной из свободных БК для заправки, которая длится в среднем Tобсл минут. При наличии очереди в Ro машин АМпокидает АЗ. Пункты задания: 1. Построить схему СМО, по ней построить граф состояний. Для первой, пятой и предпоследней вершин графа построить уравнения Колмогорова. 2. Определить, к какой группе типовых схем СМО относится заданная система обслуживания, записать формулы расчета основных характеристик этой СМО (вероятность простоя системы, вероятность отказа, вероятность того, что очередь будет не более 3-х АМ, относительную пропускную способность СМО, количество АМ, обслуженных за 1 час, за смену (8 часов), среднее время ожидания АМ в очереди, коэффициент загрузки АЗ в целом и выполнить вычисления значений этих характеристик. 3. Для этой же схемы построить имитационную GPSS-модель и запустить на компьютере(ПК) эту программу. 4. Задать в модели соответствующее время моделирования, обеспечивающее получение устойчивых (достоверных) значений характеристик моделируемой СМО. 5. Для наглядного сравнения значений характеристик, полученных путём расчёта и имитации на ПК, свести все результаты в таблицу и записать выводы по полученным результатам работы. Тут берёте 6 и 12 вариант
ПРИМЕЧАНИЕ. При аналитическом расчёте и построении GPSS-модели принять, что все случайные величины имеют Экспоненциальные (Пуассоновские ) распределения, что проявляется в GPSS на применении функций Exponential(№,0,Тсредн ), , где № -произвольное целое; Тсредн – среднее значение времени обслуживания… Решение. Вариант 6 Построить схему СМО, по ней построить граф состояний. Решение. M=2.5 АМ/мин интенсивность потока машин N=3 число каналов обслуживания Tob=4 мин Lz=5 максимальная длина очереди λ=2.5 Ам/мин –интенсивность входного потока 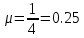 Ам/мин Ам/мин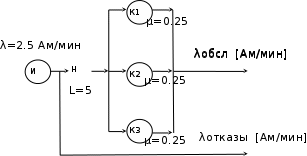 Граф состояний 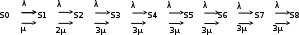 Уравнение Колмогорова для первой вершины P0∙λ=P1∙μ Уравнение Колмогорова для пятой вершины P4∙(λ+3μ)=P3∙λ+P5∙3μ Уравнение Колмогорова для предпоследней вершины P7∙( λ+3μ)= P6∙λ+P8∙3μ Определить, к какой группе типовых схем СМО относится заданная система обслуживания, записать формулы расчета основных характеристик этой СМО и выполнить вычисления значений этих характеристик. Решение. Многоканальная СМО с ожиданием (очередью) означает, что все каналы заняты и заявка ожидает, пока какой-нибудь канал обслуживания в системе не освободится. Когда канал освобождается, тогда на его вход поступает одна заявка из очереди. S0 – все каналы свободны S1 – один канал занят, остальные свободны S2 – два канала заняты, остальные свободны ….. S3 – заняты все n=3 каналов S4 – заняты все 3 канала, один транзакт в очереди … S8 – заняты все 3 канала, 5 транзактов находятся в очереди Расчет параметров по формулам.   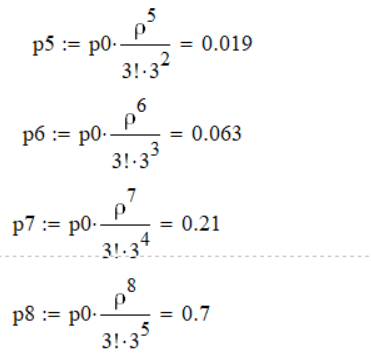   GPSS программа PARKING STORAGE 5 ; места под автостоянку BENZ STORAGE 3 ; бензоколонки GENERATE (Exponential(1,0,0.4 )) ;приезд автомобиля GATE SNF PARKING,MIMO ; если места заняты на автостоянки, то автомобиль проезжает мимо ENTER PARKING ; занять место на автостоянке ENTER BENZ ; занять бензоколонку LEAVE PARKING ; освободить автостоянку ADVANCE (Exponential(1,0,4 )) ; время заправки LEAVE BENZ ; освободить бензоколонку TERMINATE; покинуть бензоколонку MIMO LINK Poteri,FIFO; список отказанных заявок TERMINATE ; покинуть бензоколонку GENERATE 10000; время моделирования TERMINATE 1; уменьшать счетчик времен на 1 минуту START 1; начать моделирование GPSS World Simulation Report - M_4_6.1.1 Thursday, May 26, 2022 13:36:18 START TIME END TIME BLOCKS FACILITIES STORAGES 0.000 10000.000 12 0 2 NAME VALUE BENZ 10001.000 MIMO 9.000 PARKING 10000.000 POTERI 10002.000 LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY 1 GENERATE 24746 0 0 2 GATE 24746 0 0 3 ENTER 7539 5 0 4 ENTER 7534 0 0 5 LEAVE 7534 0 0 6 ADVANCE 7534 3 0 7 LEAVE 7531 0 0 8 TERMINATE 7531 0 0 MIMO 9 LINK 17207 17207 0 10 TERMINATE 0 0 0 11 GENERATE 1 0 0 12 TERMINATE 1 0 0 STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY PARKING 5 0 0 5 7539 1 4.564 0.913 0 0 BENZ 3 0 0 3 7534 1 2.999 1.000 0 5 USER CHAIN SIZE RETRY AVE.CONT ENTRIES MAX AVE.TIME POTERI 17207 0 8557.729 17207 17207 4973.400 FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE 24748 0 10000.261 24748 0 1 24727 0 10000.397 24727 6 7 24701 0 10002.094 24701 6 7 24709 0 10004.196 24709 6 7 24749 0 20000.000 24749 0 11 Выводы Вероятность обслуживания 7531/24746=0.3043 По аналитической модели 0.3 Средняя длина очереди 4.564 По аналитической модели 4.573 Среднее число занятых бензоколонок 2.999 По аналитической модели 2.999 Таким образом результаты аналитического расчета и моделирования в GPSS очень близки |
