Эл.энергетические системы. ЭЭ вар 22. Добавить титульный лист Исходные данные
 Скачать 1.22 Mb.
|
1 2 Добавить титульный лист Исходные данные Таблица 1 Параметры элементов электрической сети
Диаметры проводов: d1=15,2 мм d2=15,2 мм d3=13,5 мм 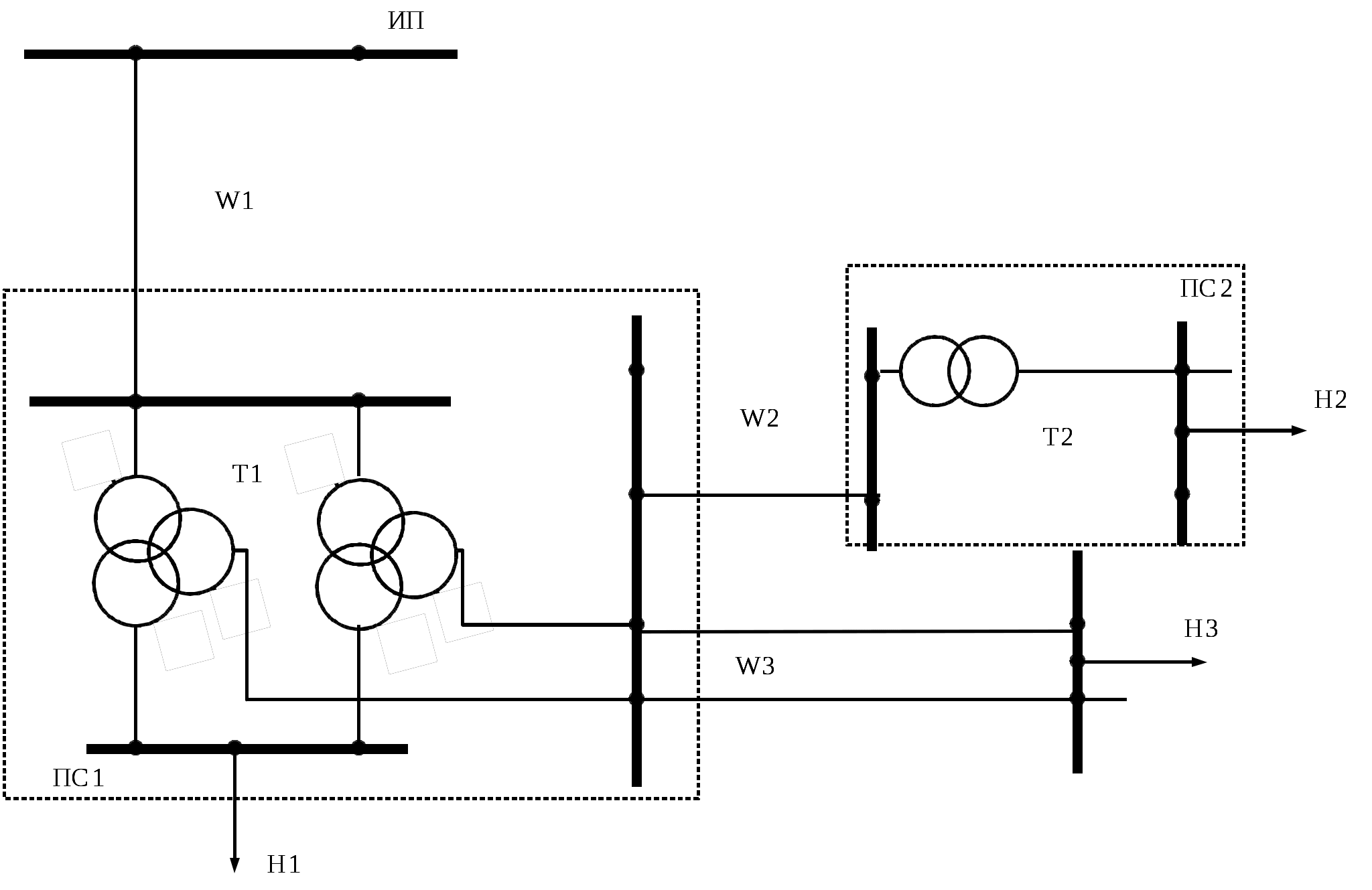 Рис. 1. Вариант схемы электрической сети №2. 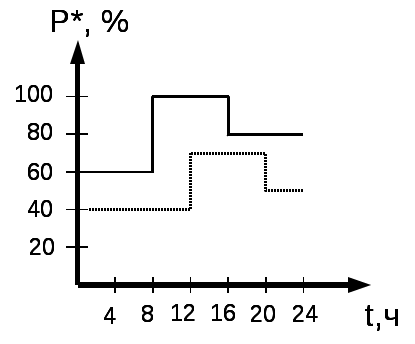 б) ГН1   в) ГН2 Г) ГН4 Рис. 2 Суточные графики нагрузки. Схема замещения участка электрической сети Требуется: 1. Составить схему замещения участка электрической сети. 2. Определить параметры схемы замещения 3 воздушных линий W1, W2, W3. 3. Определить параметры схемы замещения трансформаторов Т1 и Т2. Решение Схема замещения:  2. Определим параметры схемы замещения 3 воздушных линий W1, W2, W3. Представление элемента электрической сети его параметрами (сопротивлением и проводимостью) называется схемой замещения. Линии электропередачи при расчетах симметричных режимов электрических сетей представляются П-образной схемой замещения для одной фазы. Схема замещения ВЛ (рис.3) состоит из продольной ветви и двух поперечных ветвей с соответствующими продольными и поперечными параметрами линии. Продольные параметры– активное и индуктивное сопротивление RЛ и XЛ одной фазы линии, поперечные– это активная и емкостная проводимость GЛ и BЛ между фазой и землей (точкой нулевого потенциала).  Рис.3. Погонные сопротивления для проводов марки А, АС определяются:  ;  ,где – удельная проводимость материала провода, для марки А– 32,7….36,6 м/(Ом·мм2); Примем равной 35,5 м/(Ом·мм2) Dср– среднегеометрическое расстояние между проводами фаз, м; rпр –радиус провода, м. Среднегеометрическое расстояние между проводами фаз А, В и С определяются как  ,где DАВ, DАС, DВС– расстояние между соответствующими фазами, м. Расположении фаз в вершинах равностороннего треугольника со стороной D  R01=103/(120·35,5)=0,235 Ом/км R02=103/(120·35,5)=0,235 Ом/км R03=103/(95·35,5)=0,2965 Ом/км Х01=0,144·lg((6,5·1000·2)/15,2)+0,016=0,4305 Ом/км Х02=0,144·lg((3,0·1000·2)/15,2)+0,016=0,389 Ом/км Х03=0,144·lg((3,0·1000·2)/13,5)+0,016=0,3972Ом/км Продольные сопротивления определяются:  , Ом,  , Ом,где R0 и Х0 – погонные активное и индуктивное сопротивления проводов, Ом/км. RЛ1=(0,235·43)=10,105 Ом RЛ2=(0,235·29)=6,815 Ом RЛ3=(0,2965·31)/2=4,596 Ом ХЛ1=(0,4305·43)=18,51 Ом ХЛ2=(0,389·29)=11,281 Ом ХЛ2=(0,3972·31)/2=6,157 Ом Активная проводимость G ВЛ обусловлена потерями активной мощности из-за токов утечки через изоляцию и ионизации воздуха вокруг проводов (явление общей короны). Для ВЛ 35 кВ и ВЛ 110 кВ с сечением проводов 70 мм2 и выше эти потери незначительны и активная проводимость таких линий принимается равной нулю. Погонная емкостная проводимость ВЛ в0 См/км, обусловлена зарядными токами между фазами и между каждой фазой и землей рассчитывается по формуле: 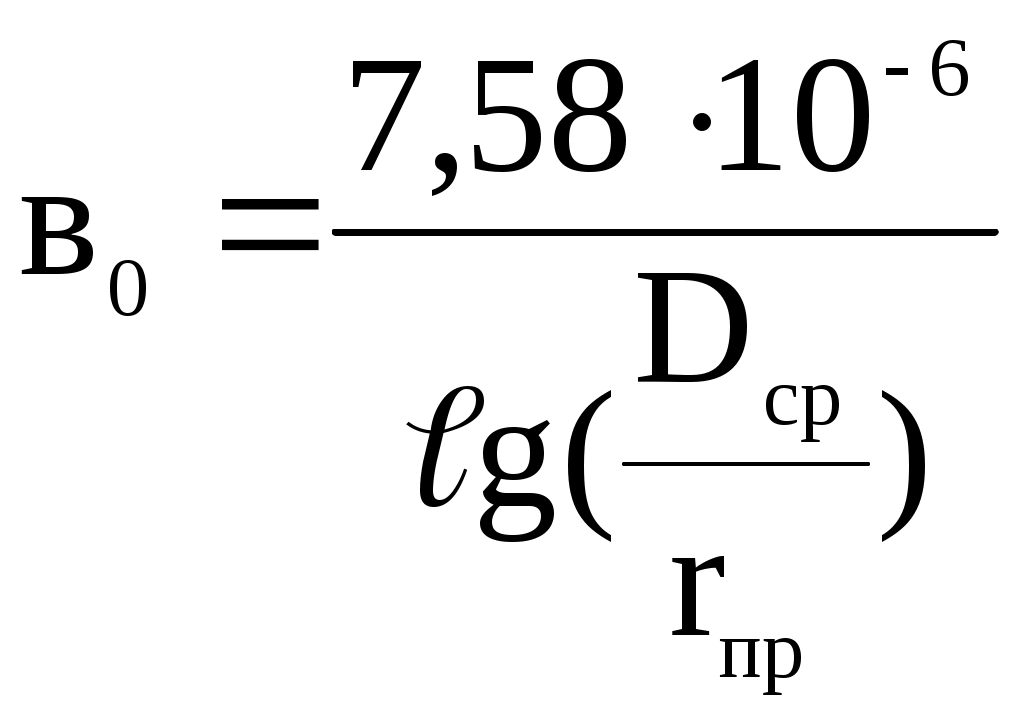 , а проводимость всей линии:  .В01=7,58·10-6/lg((6,5·1000·2)/15,2)=2,658·10-6 См/км В02=7,58·10-6/lg((3,0·1000·2)/15,2)=2,919·10-6 См/км В03=7,58·10-6/lg((3,0·1000·2)/13,5)=2,864·10-6 См/км ВЛ1=2,658·10-6·43=1,155·10-4 См ВЛ2=2,864·10-6·29=0,847·10-4 См ВЛ3=2,864·10-6·31*2=1,776·10-4 См Наличие эквивалентной емкости между фазой и землей обуславливает зарядную мощность линии QСЛ. Величина этой мощности, Мвар, определяется по выражению:  ,где UH – номинальное линейное напряжение ВЛ, кВ. QСЛ1=1102·1,155·10-4=1,398 Мвар QСЛ2=352·0,847·10-4=0,104 Мвар QСЛ3=352·1,776·10-4=0,218 Мвар Упрощенная схема замещения ВЛ представлена на рис.4. 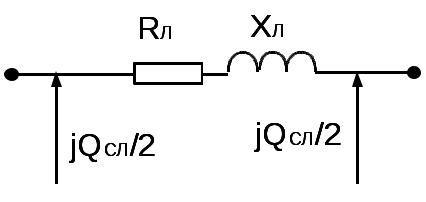 Рис.4. Величина погонных параметров линий электропередачи в зависимости от конструктивного исполнения и номинального напряжения линий приведены в справочных материалах. 3. Определим параметры схемы замещения трансформаторов Т1 и Т2. При расчетах электрических сетей двухобмоточный трансформатор представляют Г-образной схемой замещения (рис.5 а). Продольными параметрами схемы являются активные и реактивные сопротивления RТ и ХТ обмоток трансформатора.  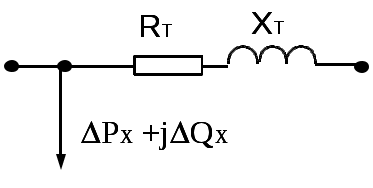 А) Б) Рис.5. Поперечными параметрами схемы являются активные и реактивные проводимости GТ и ВТ. В упрощенной схеме замещения (рис. 5 Б) поперечная ветвь представлена в виде отбора ими потерь мощности  – потерь холостого хода.Схема замещения трехобмоточного трансформатора приведена на рис.7.  Рис. 6. Поперечные параметры схемы замещения такие же, как у духобмоточного трансформатора, а продольные параметры представлены трех лучевой схемой, каждый луч которой соответствует одной из трех обмоток трансформатора. Поскольку трансформатор связывает сети разных напряжений, все его параметры приводятся к одному напряжению, к напряжению первичной обмотки. На подстанциях электрической сети первичной обмоткой является, как правило, обмотка высшего напряжения. Параметры схем замещения двухобмоточных трансформаторов рассчитываются по следующим каталожным (паспортным) данным: ST– номинальная мощность трансформатора, кВА; UВН, UНН – номинальные напряжения обмоток высшего и низшего напряжения трансформатора; PХ – потери активной мощности при холостом ходе трансформатора, кВт; IХ– ток холостого хода, %; uК – напряжение короткого замыкания, %; PК – потери активной мощности при коротком замыкании трансформатора, кВт. Для расчета параметров схемы замещения двухобмоточного трансформатора применяются формулы:  , Ом,  , Ом,  , Мвар,RT2=10-3· 115·(36,75)2/252=0,248Ом; RТ2сх=0,248 Ом ХТ2=(9,5/100)·36,752/25=5,13 Ом; ХТ2сх=5,13 Ом QТ2х=(0,5/100)·25=0,125 Мвар; QТ2х сх=0,125 Мвар GТ2=10-3· 25/36,752=18,51·10-6 См GТ2сх=18,51·10-6 См ВТ2=(0,5/100)·(25/36,752)=92,55·10-6 См ВТ2сх=92,55·10-6 См В паспортных данных трехобмоточного трансформатора дополнительно к данным двухобмоточного указывается номинальное напряжение обмотки среднего напряжения UС и три значения напряжений короткого замыкания для каждой пары обмоток: uKB-H%, uKB-C%, uKC-H%,дольные параметры трехобмоточного трансформатора определяются отдельно для каждой ветви схемы замещения. Активные сопротивления обмоток равны между собой и определяются: RТВ=RТС=RТН=  , Ом.RT1В=10-3· 200·(115)2/(2·402) =0,826 Ом; RТ2Всх=0,826/2=0,413 Ом RT1С=0,826 Ом; RT1Ссх=0,413 Ом RT1Н=0,826 Ом; RT1Нсх=0,413 Ом Напряжения короткого замыкания каждой обмотки uKi(i=B, C, H) рассчитываются по формулам  %=0,5( %+ % –  %)=(10,5+17-6)/2=10,75% %=0,5( %+ % – %)=(10,5+6-17)/2=-0,25%=0 %=0,5( %+ % – %)=(17+6-10,5)/2=6,25%=6,5Реактивные сопротивления обмоток трехобмоточного трансформатора вычисляются по выражениям ХТВ=  , Ом, ХТС= , Ом, ХТН= , Ом, ХТ1В=(10,75/100)·1152/40=35,54 Ом; ХТ2сх=35,54/2=17,77 Ом ХТ1С= 0 Ом; ХТ2сх=0 Ом ХТ1Н=(6,25/100)·1152/40=20,66 Ом; ХТ2сх=20,66/2=10,33 Ом QТ1х=(0,6/100)·40=0,24 Мвар; Qхх сх=0,24·2=0,48 Мвар GТ1=10-3· 43/1152=3,25·10-6 См ВТ1=(0,6/100)·(40/1152)=18,147·10-6 См GТ1сх=3,25·10-6 ·2=6,5·10-6 См ВТ1сх=18,147·10-6 ·2=36,294·10-6 См Два параллельно включенных трансформаторов представляются одной схемой замещения с уменьшением продольных сопротивлений RT и ХТ в два раза и увеличением в два раза поперечных составляющих – потерь холостого хода РХ и QX. Расчет потерь активной мощности и электроэнергии в электрической сети При использовании исходных данных по нагрузкам и результатам расчета параметров схемы замещения электрической сети требуется: 1. Построить суточные зимние и летние графики активных нагрузок элементов электрической сети ВЛ и силовых трансформаторов в именованных единицах. 2. Рассчитать величины активной электроэнергии, передаваемой по элементам сети в зимние, летние сутки и за год в целом. 3. Определить годовое число часов использования максимальной нагрузки годового времени потерь электроэнергии. 4. Рассчитать годовые потери электроэнергии в электрической сети по графикам электрической нагрузки и с использованием числа часов максимальной нагрузки и времени потерь. Решение 1. Построим суточные зимние и летние графики активных нагрузок элементов электрической сети: ВЛ и силовых трансформаторов в именованных единицах.  ; Рmax1=25 МВт; Рmax1=13 МВт; Рmax1=14 МВт;Таблица 2 Суточные графики активной мощности пунктов для зимы
Таблица 3 Суточные графики активной мощности пунктов для лета
2. Рассчитаем величины активной электроэнергии, передаваемой по элементам сети в зимние, летние сутки и за год в целом. Пусть для элемента электрической сети, имеющего активное сопротивление R, известен график нагрузки за период времени Т (сутки–24 час., год– 8760 час). Этот график представляется в виде ступенчатого графика по продолжительности ступени ti каждой нагрузки Рi.. Энергия, передаваемая в течении рассматриваемого периода Т через элемент сети, выразится как  ,где n– число ступеней графика нагрузки. Т/  .Эта энергия равна площади фигуры, ограниченной осями координат и графиком нагрузки. Принято число зимних суток в году равным 200, а число летних суток – 165. Таблица 4 Суточное и годовое потребление электроэнергии по элементам сети (МВт·ч)
3. Определим годовое число часов использования максимальной нагрузки годового времени потерь электроэнергии.  ,  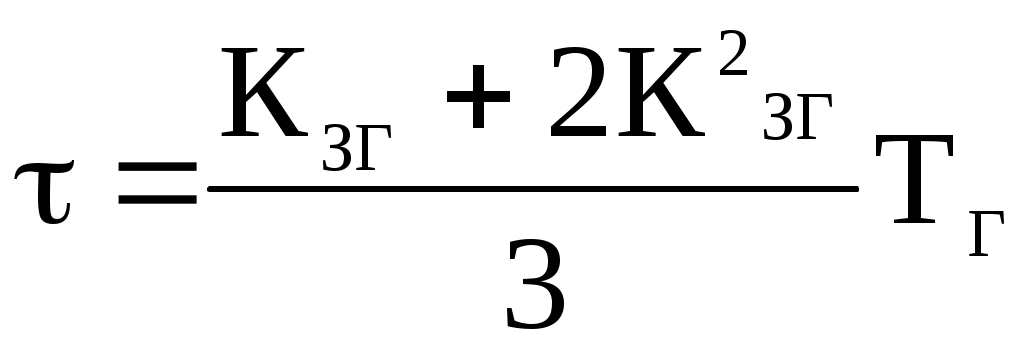;  , ч/год; ТГ=8760 ч.Таблица 5
4. Рассчитаем годовые потери электроэнергии в электрической сети по графикам электрической нагрузки и с использованием числа часов максимальной нагрузки и времени потерь. Величина постоянных потерь электроэнергии  ,где  – постоянные потери мощности элемента сети, ТВКЛ– время включения или время работы элемента.Постоянные потери мощности в ВЛ напряжением до 110 кВ и в ВЛ напряжением 110 кВ и сечением проводов свыше 70 мм2, в ВЛ напряжением 220 кВ и сечением проводов свыше 240 мм2 значительно меньше, чем переменные потери мощности. Поэтому в технических расчетах электрических сетей эти потери принимаются равными нулю. Постоянные потери мощности в силовых трансформаторах – это потери холостого хода РХ. При двух параллельно работающих трансформаторах на подстанции суммарные постоянные потери равны: Р’Т=2РХ. Переменные потери электроэнергии в элементах электрической сети определяются по графикам электрических нагрузок. Переменные потери мощности в рассматриваемом элементе для каждого i-го интервала времени составит  .Переменные потери электроэнергии за время Т составят 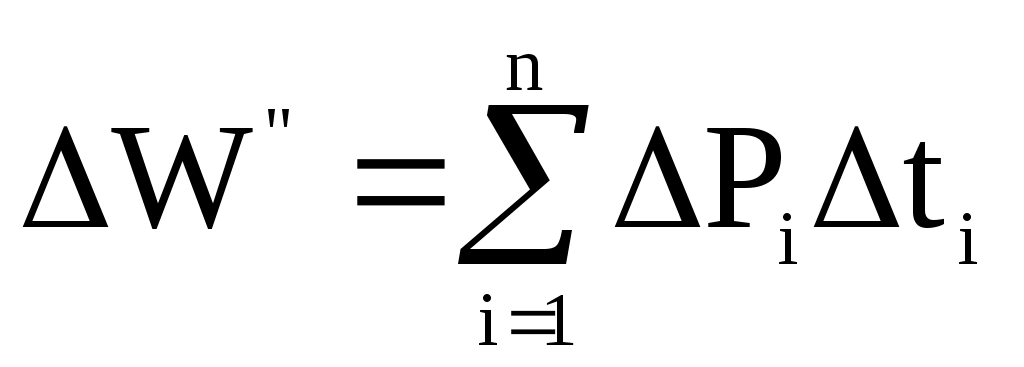 .Переменные потери мощности в интервале ГН в сопротивлениях обмоток двухобмоточных трансформаторов определяются по формулам:  или 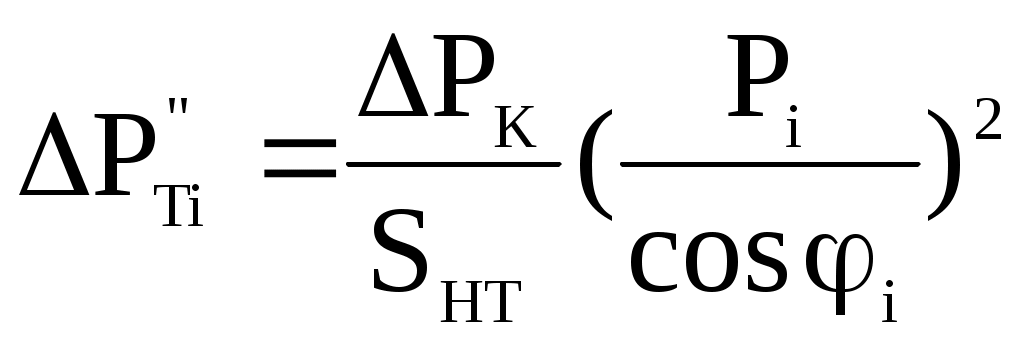 .Переменные потери мощности в i-м интервале ГН в трехобмтоточных трансформаторах определяется по формулам  где РiB, РiС, РiН – активная мощность, протекающая соответственно по обмоткам высокого, среднего и низкого напряжения; cosiB, cosiС, cosiН– коэффициенты реактивной мощности нагрузок обмоток соответственно высокого, среднего, низкого напряжения; UНВ – номинальное напряжение обмотки высокого напряжения. При двух параллельных трансформаторах на подстанции переменные потери электроэнергии уменьшаются в 2 раза. При определении суммарных годовых потерь электроэнергии принято число зимних суток в году равным 200, а число летних суток – 165. Таблица 6 Потери электроэнергии в обмотке НН Т1(МВт·ч)
Потери электроэнергии в обмотке СН Т1(МВт·ч)
Потери электроэнергии в обмотке ВН Т1(МВт·ч)
Потери в трансформаторах за год: 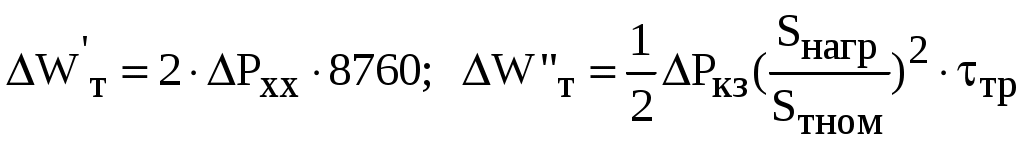 Потери в Т1 с учетом графика нагрузки:  =2·0,043·8760+79,23+133,468+359,97=1325,768 МВт·ч.Потери Т1 с использованием числа часов максимальной нагрузки и времени потерь WТ1=2·0,043·8760+(1/2)·0,2((252/(0,9·40)2·3289+272/(0,91·40)2·4281+ 522/(0,905·40)·3775)= 1926,45 МВт·ч. Таблица 7 Потери электроэнергии в обмотках Т2(МВт·ч)
Потери в Т2 с учетом графика нагрузки: 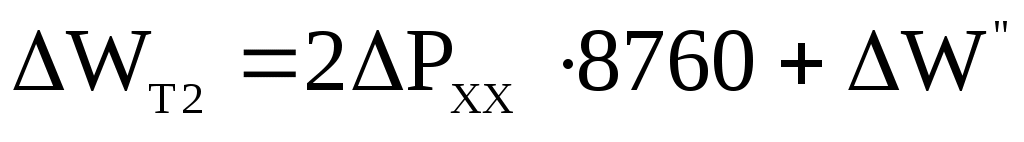 =0,025·8760+162,17=381,17 МВт·чПотери Т2 с использованием числа часов максимальной нагрузки и времени потерь WТ2=0,025·8760+0,115·132/(0,91·25)2·4599=342,65 МВт·ч Таблица 8 Потери электроэнергии в ВЛ1 (МВт·ч)
 (522·10,105·3775)/(110·0,905)2=10454,59 МВт·чТаблица 9 Потери электроэнергии в ВЛ2 (МВт·ч)
 (132·6,815·4599)/(35·0,91)2=5221,52 МВт·чТаблица 10 Потери электроэнергии в ВЛ3 (МВт·ч)
 (142·4,596·3994)/(35·0,91)2=3546,71 МВт·чЧисло часов использования максимальной нагрузки ТМ– это время в течении которого при максимальной нагрузки Рmax передается такое же количество электроэнергии, как и при переменной нагрузке за действительное время Т. Годовое число часов электроэнергии ТМГ определяется:  , ч/год,где WГ – энергия, передаваемая по электрической сети за время ТГ=8760 ч. Время потерь – это время, в течении которого потери электроэнергии в элементе с сопротивлением R при максимальной нагрузке равно потерям электроэнергии в этом элементе при действительно переменной нагрузке за действительное время Т. Допускается определять годовое время потерь по эмпирической формуле  , ,  ,где КЗГ – коэффициент заполнения годового ГН,  – переменные потери мощности в элементе сети при максимальной нагрузке.Таблица 2 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
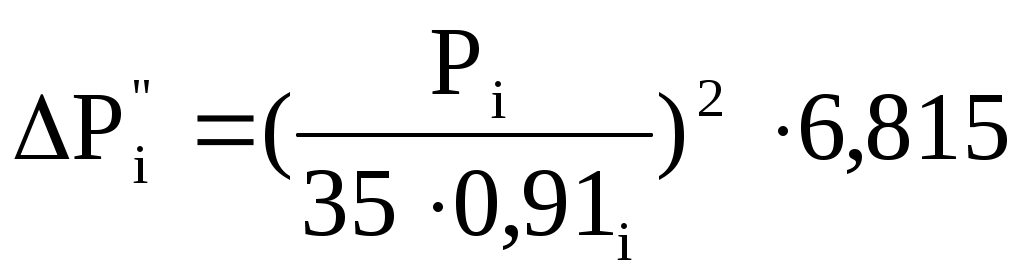-зима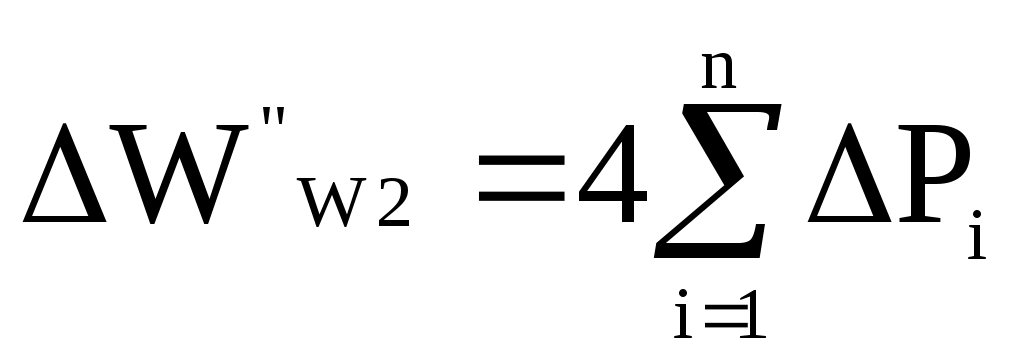
зима
зима