Применение кремниевых ФЭУ в персональной дозиметрии
Кремниевые фотоумножители (Si-ФЭУ) в последнее время получают растущее внимание в качестве альтернативы традиционным фотоумножителям для обнаружения низких потоков фотонов благодаря ряду типичных для твердотельных детекторов преимуществ, таких как компактность, долговечность, простота использования, низкое рабочее напряжение и нечувствительность к магнитным полям [22], высокая эффективность и очень низкое временное разрешение. Благодаря этим преимуществам Si-ФЭУ обычно используются в качестве световых датчиков в быстрых сцинтилляционных
детекторах для электромагнитных и рентгеновских лучей, которые широко используются в ядерной медицине и в экспериментах по физике высоких энергий.
Si-ФЭУ представляет собой матрицу малогабаритных чувствительных элементов, называемых микроячейки (пиксели), которые идентичны, одиночны и соединены параллельно. Каждая микроячейка представляет собой p-n – переход со своим собственным последовательным резистором (рисунок 2.7). Для обеспечения высокого коэффициента усиления, микроячейки работают в режиме Гейгера [23].
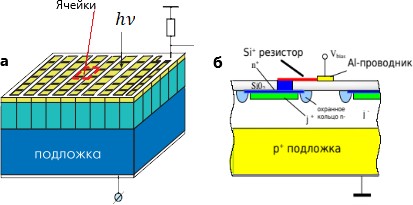
Рисунок 2.7 – Si-ФЭУ: а) конструкция, б) топология электрического поля внутри кристаллического слоя [24]
Каждая микроячейка Si-ФЭУ создает импульсный выходной сигнал при обнаружении единичного фотона. Таким образом, общий выходной сигнал кремниевого фотоумножителя представляет собой сумму выходных сигналов с каждой микроячейки. Кремниевые фотоумножители обладают высокой обнаружительной способностью необходимой для счета фотонов и используются в различных применениях, в которых требуется детектирование очень слабых световых сигналов на уровне единичных фотонов [24].
Численное моделирование взаимодействий излучения с веществом
Метод Монте-Карло
Для изучения процесса прохождения частиц в веществе удобным способом является метод Монте-Карло. Метод Монте-Карло – численный метод, в котором используются числовые значения случайных величин с заданными законами распределения вероятностей. Другие общепринятые названия – метод статистического моделирования или метод случайных испытаний. Метод Монте-Карло можно понимать, как численный эксперимент на компьютере [25]. Решение какой-либо задачи методом Монте-Карло состоит в численной реализации ансамбля некоторых случайных величин или случайных событий.
Статистическая обработка этого ансамбля дает решение поставленной задачи.
В настоящее время метод Монте-Карло применяется практически во всех естественных науках, в технике, экономике, даже в сфере гуманитарных наук. Впервые он был использован в конце 40-х годов ХХ века в связи с нейтронной физикой и разработкой ядерного оружия. Для применения метода Монте-Карло в какой-либо конкретной предметной области требуется знание некоторых разделов теории вероятностей и математической статистики, а также умение программировать на языках высокого уровня (Fortran, C++). В разных прикладных областях разработаны сложные программные комплексы для решения задач методом Монте-Карло.
Метод Монте-Карло традиционно применяется в теории ядерных реакций при промежуточных и высоких энергиях, так как является единственным подходом, позволяющим описать ядерную реакцию в целом, с учетом большинства каналов реакции и с точностью, приемлемой для многих приложений [26].
Развитие каскадной лавины внутри ядра трактуется в классическом приближении: в терминах «траекторий» и «координат точек взаимодействия», во многом алгоритмически аналогично описанному выше моделированию каскадов
в веществе. Налетающая частица высокой энергии испытывает взаимодействие с внутриядерным нуклоном, и продукты этого взаимодействия инициируют дальнейшее развитие внутри ядерного каскада. Результатом моделирования являются быстрые вторичные частицы, вылетевшие из ядра и возбужденное остаточное ядро, испытывающее последующее девозбуждение согласно соответствующим ядерным моделям (испарительной, Ферми-развала, деления и др.).
Однако, поскольку развитие каскада происходит в ядерном веществе, к процессу моделирования учитываются многие квантовые эффекты, такие как: фермиевское движение внутриядерных нуклонов, принцип Паули и др. При моделировании взаимодействий «ядро-ядро» рассматривают развитие каскада во времени [27].
Отдельную проблему представляет описание взаимодействия элементарных частиц в каскаде, где находят применение современные теории и модели. Как правило, описание ядерных реакций высоких энергий представляет весьма сложную задачу и является предметом исследований. Но в настоящее время разработаны программные комплексы для моделирования ядерных реакций методом Монте-Карло, которые обеспечивают достаточную точность и пригодные для их использования в составе других программных систем: FLUKA, GEANT4, MARS, MCNPX, PHITS и 5HIELD.
К описанию ядерных реакций существуют два основных подхода: эксклюзивный и инклюзивный. Рассмотрим ядерную реакцию с образованием пвторичных частиц
а+b→ 1+2+... + п (3.1.1)
Эксклюзивный подход претендует на описание индивидуальных характеристик всех вторичных частиц и остаточных ядер. При этом должны соблюдаться все законы сохранения в каждом акте взаимодействия.
При инклюзивном подходе этот процесс трактуется так
a +b→ с+ X, (3.1.2)
где с – рассматриваемая частица определенного типа, а X обозначает неидентифицируемые продукты реакции, образующиеся вместе с частицей с. Для инклюзивного описания взаимодействий используют так называемое инклюзивное одночастичное инвариантное дифференциальное сечение реакции. При моделировании ядерных реакций методом Монте-Карло с использованием инклюзивных дифференциальных сечений законы сохранения выполняются лишь в среднем по ансамблю.
Метод Монте-Карло в задачах прохождения частиц в веществе сводится к пошаговому моделированию (трассировке) движения частицы через заданные объемы: вычисление ее координат в семимерном пространстве (x, y, z, t, px, py, pz). Свободный пробег, результат столкновения (потеря энергии или рассеяние), а также характеристики частицы после столкновения (энергия и направление движения рассеянной частицы) разыгрываются из соответствующих вероятностных распределений, описываемых дифференциальными сечениями соответствующих элементарных процессов. При этом значения дифференциальных сечений взаимодействий могут быть как экспериментальными, так и теоретически рассчитанными [28]. Приведем простой пример процедуры моделирования. На рисунке 3.1 схематически изображено дерево адронного каскада в сложной макроскопической мишени, например, в мишени импульсного источника нейтронов или в модуле орбитальной станции.
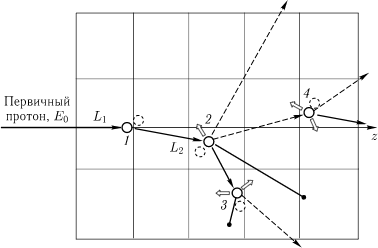
Рисунок 3.1 – Дерево адронного каскада в макроскопической мишени
Мишень на рисунке 3.1 схематически представлена прямоугольником, разделенным на несколько геометрических зон. На деле, геометрия компьютерной модели мишени будет весьма близкой к реальной мишени и будет иметь достаточно сложную конфигурацию. Это можно достичь методами аналитической геометрии в трехмерном пространстве. Конфигурация мишени фиксируется в лабораторной декартовой системе координат Оxyz. Каждая ее геометрическая зона может иметь материалы различного химического состава.
Дерево, изображенное на рисунке, включает 4 шага ядерного взаимодействия. Сплошными стрелками показаны вторичные каскадные протоны, пунктиром – каскадные нейтроны. Точками изображены остановки протонов из-за ионизационных потерь и остаточные ядра – продукты ядерных взаимодействий. А короткие открытые стрелки изображают испарительные нейтроны, у которых траектории не нарисованы, чтобы не загромождать рисунок.
Подчеркнем, что каскадное дерево на рисунке представляет всего лишь один, единственный элемент ансамбля событий взаимодействия первичного протона с мишенью. Отдельный элемент ансамбля не дает решения задачи методом Монте-Карло. Только промоделировав и обработав довольно большой ансамбль событий, можно получить физический результат, к примеру, построить энергетический спектр нейтронов, вылетающих из мишени.
Рассмотрим кратко процедуру моделирования дерева на рисунке 3.1. Первичный протон с энергией E0
1 ГэВ влетает в мишень вдоль оси Zлабораторной системы в точке с координатами r0= (0, 0, 0). Как известно, длина свободного пробега до ядерного взаимодействия подчиняется экспоненциальному распределению. Техника метода Монте-Карло позволяет получить конкретное выборочное значение длины пробега, то есть «разыграть» длину свободного пробега L1до первого ядерного взаимодействия.
После надо разыграть тип взаимодействия, происходящего в точке с координатами r1= (0, 0, L1)– упругое или неупругое, для чего используются
ядерные сечения σtot и σin. Очевидно, вероятность неупругого взаимодействия равна отношению σin/ σtot.
Пусть разыгралось упругое ядерное рассеяние. Используя распределение вероятностей угла упругого рассеяния, разыгрываем направление движения протона Ω1 (направление в трехмерном пространстве задается в зависимости от контекста) после рассеяния. Далее двухчастичная релятивистская кинематика дает значения энергий рассеянного протона и ядра отдачи.
Действуя далее аналогичным образом, разыгрываем длину пробега L2до следующего взаимодействия и вычисляем его координаты r2= r1+ Ω1 L2.
Пусть в точке r2происходит неупругое ядерное взаимодействие — ядерная реакция. Для расчета характеристик продуктов реакции в состав программного комплекса должна входить подсистема моделирования ядерных реакций методом Монте-Карло. При обращении к подсистеме моделирования ядерных реакции мы получаем индивидуальные параметры всех вторичных частиц и остаточного ядра (энергии, углы вылета и т.д.), т.е. получаем реализацию отдельной реакции из ансамбля ядерных реакций. Например, на рисунке 3.1 видно, что во втором шаге ядерного взаимодействия образуются два протона, два каскадных и один испарительный нейтрон.
В дальнейшем судьба этих вторичных частиц прослеживается аналогичным образом. Некоторые из них испытывают ядерное взаимодействие, другие вылетают на мишени или поглощаются из-за ионизационных потерь, также возможны и другие процессы, например, рождение и распад мезонов.
Статистическая обработка всего ансамбля событий типа, изображенного на рисунке 3.1, позволяет получить физические результаты, такие как потоки и спектры частиц внутри и вне мишени, распределение по объему мишени выделившейся энергии и радиоактивных ядер-продуктов, т.е. активацию мишени.
Так осуществляется (в общем виде) моделирование методом Монте-Карло процесса взаимодействия частиц со сложными макроскопическими мишенями [29].
|
 Скачать 352.38 Kb.
Скачать 352.38 Kb.

